摘  要： 简要分析了径向基函数(RBF)神经网络。在此基础上，介绍了K-均值聚类算法的神经网络、C-均值聚类算法的神经网络和PAM聚类算法的神经网络三种聚类算法的RBF神经网络。展望了基于聚类的RBF神经网络设计的发展趋势。
关键词： 聚类； RBF神经网络； 发展趋势

    径向基函数(RBF)神经网络是前向型神经网络[1]，能够以任意精度逼近于任意函数。因为RBF网络结构相对简单、非线性逼近能力强和收敛速度较快，现在已经广泛应用在工业智能控制和系统优化、通信系统的信号以及信息处理等诸多领域。对该网络的深入研究也越来越受到国内外学者的共同关注。而聚类分析[2-3]是一种对数据进行分析和建模的重要方法，即将没有明显规律的数据源，依据某些特性，将数据划分到有区别的数据类中，所采用的聚类算法就是聚类分析研究的重点。本文综述了三种聚类算法是如何构造RBF神经网络。
1 RBF神经网络结构及其原理
    RBF神经网络的原理[4]是模拟人脑中局部协调和相互覆盖接收范围的神经网络构造。它是一种三层前向网络，由输入量到输出量的映射存在非线性，而隐含层空间到输出空间的映射却是线性的，从而提高了学习速度，同时也避免了局部极小问题。RBF神经网络结构如图1所示。它具有n个输入节点、m个隐含节点和1个输出节点。
 
 
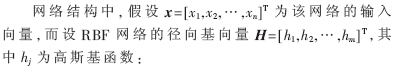
    构造和训练RBF神经网络就是要使它经过学习来确定每个隐层神经元基函数的中心和宽度，然后再利用最小二乘或其他方法求出隐含层到输出层的权值向量，从而构建出所研究系统的输入到输出的映射关系。
2 聚类的RBF神经网络设计
    对RBF神经网络来说,隐层节点中心和基函数宽度的初始值的确定会直接影响神经网络的收敛速度,因此选择合适的两个参数的初始值可以提高收敛速度,其选择方法有很多，比如有梯度下降法、模糊理论算法和自适应模糊等方法。而本文就是综述K-均值聚类算法、C-均值聚类算法和PAM聚类算法,利用不同的聚类分析算法得到隐层节点中心和基函数宽度,从而构造和训练出合适的RBF神经网络。

　　计算过程从一个随机的聚类中心开始，通过寻找目标函数的最小点，反复调整聚类中心和各个样本的隶属度，在Jc的局部最小点处收敛，最终达到确定样本类别。
 
近，即d(Pj,Ph)≥d(Pj,Pj2)，则Pj2是Pj的第二最近中心点。此时若将Ph替换Pi作为中心点，则Pj∈Pj2所代表的组，因此就Pj来说替换的代价为Cjih=d(Pj,Pj2)-d(Pj,Pi)；

3 发展趋势
    要进一步提高聚类算法对RBF神经网络隐层节点中心和基函数宽度的确定，需要优化改进现有的聚类算法，以提高学习性能。因此，出现了一些在原聚类算法基础上改进的聚类算法[8-10]，弥补了样本分析在聚类过程中存在的某些不足,将聚类算法的性能发挥得更加充分，能更有效地与RBF神经网络结合起来。
参考文献
[1] 苏美娟.径向基函数神经网络学习算法研究[D].苏州:苏州大学，2007.
[2] CHIU S L. Fuzzy model identification based on cluster estimation[J]. Journal of Intelligent and Fuzzy System，1994，2(3)：1240-1245.
[3] 满春涛，李晓霞，张礼勇.一种基于ACO的RBF神经网络训练方法[J].哈尔滨理工大学学报，2008，13(1):59-61,65.
[4] 刘金琨.先进PID控制及其MATLAB仿真[M].北京:电子工业出版社，2003.
[5] 吴晓蓉.K-均值聚类算法初始中心选取相关问题的研究[D].湖南:湖南大学，2008.
[6] 何迎生，段明秀.基于模糊聚类的RBF分类器的设计与实现[J].重庆科技学院报，2009，12(2):101-103.
[7] 段明秀，孙可.基于PAM聚类方法的RBF神经网络设计[J].沈阳师范大学学报,2009，27(4):440-443.
[8] 朱长江，张缨.模糊Ｃ-均值聚类算法的改进研究[J]. 河南大学学报，2012，42(1):92-95.
[9] 李春富，郑小青，葛铭.基于改进聚类算法的RBF网络及其应用[J].南京工业大学学报，2011，33(6):72-76.
[10] 庞振,徐蔚鸿.一种基于改进K-means的RBF神经网络学习方法[J].(2011-07-14).[2012-01-20]：http://www.cnki.net/kcms/detail/11.2127.TP.20110714.1550.036.html.