摘  要： 针对一维阈值分割只考虑图像的灰度级而不考虑像素的空间信息且需要目标函数的问题，根据最优进化图像阈值分割算法的基本思想，提出了一种无目标函数的二维图像阈值分割算法框架（2D-OEA）。2D-OEA将每个图像二维信息向量看作一个染色体，假设最优进化方向存在，建立进化方向更新模型；然后定义了染色体编码规则，通过简单随机采样初始化种群，再对种群进行交叉变异运算、适值计算、选择和阈值修正，得到稳定的最优二维阈值。分别从理论和实验分析了假设和模型的合理性。实验结果表明，假设和进化方向更新模型合理，2D-OEA快速、稳定且有效，分割结果优于OEA。
关键词： 阈值分割； 图像分割； 遗传算法； 二维直方图； 灰度级

　阈值分割是图像处理的一种重要方法，在图像处理领域有着广泛的应用，如文本处理、粒子计数、细胞运动估计和目标识别等。阈值分割的效果决定了后继图像处理和图像分析的效果。阈值分割是指找到一个能把图像分割为目标和背景的最优阈值。最优阈值通常很难确定，学者们根据不同的标准提出了大量阈值分割的方法。ZHANG Y J[1]分析了1995年以前的大部分图像分割方法，并将这些方法分成了三大类。SEZGIN M和SANKUR B[2]分析了2003年以前的40种主要的阈值分割方法，根据分割时考虑的图像信息，将这此方法分为直方图形状、测试空间聚集度、熵、目标属性、空间相关性和局部灰度面6类。近年来，出现了许多新的阈值分割方法，如基于II型模糊逻辑理论的方法[3]、基于图谱划分理论的方法[4]和基于能量函数最优化的方法[5]等。图像阈值分割算法一般根据其他理论或某些标准定义一个目标函数，然后通过求解最优化问题得到最优阈值。LUESSI M、EICHMANN M、SCHUSTER G M和KATSAGGELOS[6]将这些目标函数分成两类，并提出了一个求解的算法框架，该框架不仅可处理现有的阈值分割问题，还可以拓展到多级阈值情况。林正春、王知衍和张艳青[7]根据大多数阈值分割算法需要定义目标函数的特点，结合进化算法，提出了一种不需要目标函数的图像阈值分割算法——最优进化图像阈值分割算法（OEA）。
　一般的图像阈值分割算法仅利用了图像的一维信息，通常是灰度信息。当目标信息和背景信息的均值相差较远且各自的标准差较小时，即直方图的谷点明显时，一维阈值分割方法能较好地将目标和背景分开。若根据一维信息无法找出最优阈值，解决方法主要有两种：一是通过直方图转化，使得谷点更明显；二是考虑更多的图像信息，如图像中各像素的空间信息，即二维图像阈值分割算法。二维图像阈值分割算法源于AHUJA V和ROSENFELD A[8]的研究以及KIRBY R L和ROSENFELD A[9]的研究。学者们根据二维阈值分割的思想，结合其他理论，提出了许多新的图像阈值分割算法，如二维最大熵遗传算法[10]、二维灰度直方图非模糊性最大化方法[11]、基于二维Tsallis-Havrda-Charvát熵的方法[12]、基于改进二维最大熵及粒子群递推的方法[13]和基于二维最小Tsallis交叉熵的方法[14]等。本文针对一维图像阈值分割算法一般不考虑像素的空间信息且需要目标函数的问题，根据OEA的思想，提出了一种通用的、无目标函数的二维图像阈值分割算法框架（2D-OEA）。
1 二维最优进化图像分割算法
　遗传算法（GA）是受生物进化理论的启发而提出的，HOLLAND J[15]首次使用了遗传算法一词。GA原理简单，不涉及复杂的数学知识，是一种有效的求解最优化问题的方法。许多学者将GA和其他理论相结合，提出了很多有效的阈值分割方法。OEA[7]也是根据遗传算法理论提出的一种新的图像阈值分割算法。与一般方法不同，OEA不需要将阈值分割问题转化来得到目标函数，而是将图像中的每个像素看作一个染色体，通过个体的进化找到最优阈值。与其他一维阈值分割方法类似，OEA也只利用了图像一维信息。本文根据OEA的基本思想，结合图像的二维信息，提出二维最优进化图像阈值分割算法（2D-OEA）。
1.1 阈值更新模型
　图像阈值分割算法一般根据其他理论将阈值分割问题转化，以得到目标函数，再辅以最优化方法进行求解。目标函数的作用在于提供一个收敛方向，在进化算法中起到进化方向的作用，引导种群向着特定的方向进化。实际上，生物的进化并没有“目标函数”的指引，生物能自觉地向着最优的进化方向进化。
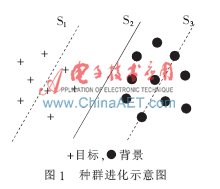
图像中的每个像素可看作是一个染色体，像素对应的信息经过编码后得到染色体的基因。每代进化后，种群聚集的地方即为种群当前实际的进化方向。图像可看作由目标和背景组成，因此种群中有两类个体，而阈值即为分割两类不同个体的分割面。如图1所示，若阈值选在分割面S1处，当种群向着S1进化时，代表背景的个体离分割面较远，进化后种群的聚集地将偏向S1的右方；若阈值选在分割面S3处，则进化后种群的聚集地将偏向S3的左方。随着进化方向不断地修正，当分割面恰好将两类个体分开时（即S2处），种群的进化才能达成一致，稳定地向该方向进化。

　因此，种群存在一个最优进化方向T，种群总可以找到最优进化方向。由于最优阈值事先无法确定，因此种群最初的进化也无法进行。给定一个初始阈值T0，由于最优进化方向存在，因此无论如何设定初始阈值，种群都应稳定地收敛到最优阈值。种群进化过程中受随机因素ε的影响，每次进化存在随机误差εi，随机误差采用正态分布模型。种群的进化模型为：

1.2 2D-OEA
　在2D-OEA中，染色体对应于一个二维向量，对该向量编码后得到染色体的基因序列。2D-OEA是通用的二维阈值分割算法，不失一般性，本文选取常用的图像二维信息（灰度和灰度均值）进行实验。若图像的灰度级为L，则灰度均值的范围为0~L。灰度—灰度均值二维直方图如图2所示，图2（b）为图2（a）的灰度-灰度均值二维直方图及分区，图2（c）为分区俯视图。在阈值向量处用十字线将二维直方图分成4个矩形区域，1区和3区分别代表目标和背景，2区和4区均代表边界和噪声。

　为了检测算法的性能，选择一幅测试图（如图3（a）所示）进行测试。设置不同的初始阈值，2D-OEA的计算过程如图4所示。由图4可知，无论初始阈值如何设置，2D-OEA得到的阈值都较稳定，收敛性较好。图4的实验结果证明，最优进化方向存在，2D-OEA实现了无目标函数的图像二维阈值分割。2D-OEA初始阈值的设定对算法的计算速度有一定的影响，若设为随机值，当初始阈值距离最优阈值较远时，需要较多的迭代次数来平滑此差距。图像由目标和背景组成，因此目标和背景的比应为0.5左右。将初始阈值设为区间中点将提高算法收敛的速度，因此下面的实验初始阈值设为（0.5L，0.5L）。对图3（a）进行1 000次实验，最优阈值向量均值为（121.430 0，119.999 0），每次实验得到的最优阈值向量与最优阈值向量均值的2-范数均值为1.758 9，2-范数方差为1.410 4；每次实验进化代数均值为3.215 0次，方差为0.924 8。实验说明，2D-OEA收敛较快，收敛的稳定性较好。

　本文针对一维图像阈值分割算法只考虑图像一维信息和传统二维图像阈值分割算法需要目标函数的问题，根据OEA的思想，提出了一种通用的，无目标函数的二维图像阈值分割算法框架（2D-OEA）。2D-OEA对二维图像信息编码，然后对种群进行交叉变异运算，计算出种群的适值，再根据选择机制选择出新的种群，提出了阈值更新模型和阈值修正方法，提高了算法的稳定性。本文从理论上分析了算法的合理性，并以图像的灰度-灰度均值二维直方图为例，通过实验验证了算法的合理性。采用5幅常用的测试图对2D-OEA进行测试，实验结果表明，2D-OEA快速、稳定且有效，其分割结果优于OEA。
　实验中也发现了2D-OEA的一些起不足，如采用两类的中点修正阈值显然不是最优的修正方法，采用简单随机采样不能保证最好地体现图像的二维信息特征。今后将致力于解决这些问题，继续完善进化方向更新模型。
参考文献
[1] ZHANG Y. J. A survey on evaluation methods for image segmentation[J]. Pattern Recognition， 1996， 29（8）： 1335-1346.
[2] SEZGIN M， SANKUR B. Survey over image thresholding techniques and quantitative performance evaluation[J]. Journal of Electronic Imaging， 2004， 13（1）： 146-165
[3] YUKSEL M E， BORLU M. Accurate segmentation of dermoscopic images by image thresholding based on type-2 fuzzy logic[J]. IEEE Transactions on Fuzzy Systems， 2009， 17（4）： 976-982
[4] TAO W B， JIN H， ZHANG Y M， et al. Image thresholding using graph cuts[J]. IEEE Transactions on Systems Man and Cybernetics Part a-Systems and Humans， 2008， 38（5）： 1181-1195
[5] SAHA B N， RAY N. Image thresholding by variational minimax optimization[J]. Pattern Recognition， 2009， 42（5）： 843-856.
[6] LUESSI M， EICHMANN M， SCHUSTER G M， et al.Framework for efficient optimal multilevel image thresholding[J]. Journal of Electronic Imaging， 2009， 18（1）.
[7] Lin Zhengchun， Wang Zhiyan， Zhang Yanqing. Optimal evolution algorithm for image thresholding[J]. Journal of Computer-Aided Design & Computer Graphics， 2010，22（7）：1201-1206.
[8] AHUJA N， ROSENFEID A. A Note on the use of second-order gray-level statistics for threshold selection[J]. IEEE Transactions on Systems， Man and Cybernetics 1978， 8（12）： 895-898.
[9] KIRBY R L， ROSENFELD A. A Note on the use of （gray level， local average gray level）space as an aid in threshold selection [J]. IEEE Transactions on Systems， Man and Cybernetics， 1979， 9（12）： 860-864.
[10] 陈果，左洪福.图像分割的二维最大熵遗传算法[J]. 2002，14（6）：530-534.
[11] Qing Wang， Zheru Chi， Zhao R. Image thresholding by maximizing of nonfuzziness of the 2D grayscale histogram[J]. Computer Vision and Image Understanding， 2002， 85（2）： 100-116.
[12]    SAHOO P K， ARORA G. Image thresholding using two-dimensional Tsallis-Havrda-Charvat entropy[J]. Pattern Recognition letters， 2006， 27（6）： 520-528
[13]  吴一全，张金矿.基于改进的二维最大熵及粒子群递推的图像分割[J].计算机辅助设计与图形学学报， 2008，20（10）：1338-1344.
[14] TANG Y G， DI Q Y， ZHAO L X， et al. Image thresholding segmentation based on two-dimensional minimum Tsallis-cross entropy[J]. Acta Physica Sinica， 2009， 58（1）： 9-15.
[15] HOLLAND J. Adaptation in natural and artificial systems[M]. University of Michigan， 1975.
[16] OTSU N. A threshold selection method from gray level histogram  [J]. IEEE Transactions on System， Man and Cybernetics， 1979， 9（1）： 62-67
[17] KITTLER J. ILLINGWORTH J. Minimum error thresholding[J]. Pattern Recognition， 1986， 19（1）： 41-47
[18] BOSCO G L. A genetic algorithm for image segmentation[C]. 11th International Conference on Image Analysis and rocessing，2001： 262-266.
[19] Zhao Xin， LEE M E， KIM S H. Improved image thresholding using ant colony optimization algorithm[C].Proceedings of Dalian， 2008： 210-215
[20] Lin Zhengchun， Wang Zhiyan， Zhang Yanqing. Image thresholding using particle swarm optimization[C]. Proceedings of MultiMedia and Information Technology， MMIT′08 International Conference， 2008： 245-248.