LDPC码[1]（Low-Density Parity-Check Code）已经被证明是实用的好码，因其优异的纠错性能和高效的迭代译码算法而具有广阔的应用前景。QC-LDPC码(Quasi-Cyclic LDPC Code)是根据系统化构造方法构造的一类非常重要的LDPC码，目前已经成为LDPC码硬件实现研究的热点。空间数据系统委员会（CCSDS）推荐了多种码长和码率的QC-LDPC码作为卫星通信和深空通信的信道编码标准[2]。

    为满足不同码率的需要，同时考虑译码器应当具有低复杂度和低功耗，本文设计了一种基于改进分层译码算法的译码器结构，以满足实际需要。

其中每个子矩阵Ai，j都是一个z×z的循环方阵，此方阵只可能是零矩阵、单位阵或者单位循环移位后的矩阵。
    置信传播算法[3-4]BP(Belief-propagation decoding algorithm)是很重要的一类基于LDPC码的译码算法，因其具有严格的数学结构和良好的性能，可以对译码算法的性能做定量分析。修正最小和（MMSP）译码算法[5]实际采用的是BP算法机制，虽然具有较低复杂度并保持良好的性能，但在实际应用中会占用大量硬件资源，且译码延时较长。基于OMS(Offset Min-Sum)的分层译码算法[6]能保证信息马上得到传递，从而改进信息的收敛性。


2 译码器的FPGA实现
2.1 译码器结构总体设计
    译码器有三种不同的译码结构：全并行结构、串行结构和部分并行结构。部分并行结构避免了全并行结构资源消耗过大、硬件实现难度大的缺点，同时译码速率比串行结构快得多，十分适于实际应用。然而，部分并行结构对校验矩阵中非零元素的分布有特定的要求，而现有的大多数LDPC码其校验矩阵中“l”的分布具有随机性，因此译码器采用部分并行结构十分困难。
    QC-LDPC校验矩阵H的每行校验子矩阵中所有行对应的校验节点自然地被划分为一个校验节点集合，而且任意两个集合Li和Lj，满足Li∩Lj=?准。集合Li中的任意两个校验节点Ci、Cj不与相同的变量节点相连，因此可以并行地对每一集合中的校验节点Ci进行更新。
    为此，借鉴全并行结构的思想，对串形结构进行修改，增加译码器中的并行节点更新模块（NUU）个数，得到的部分并行结构共有b个NUU单元。b为循环子矩阵的行数。
    QC-LDPC并行译码器模块主要由以下几个模块构成：输入缓冲模块、控制模块、节点更新模块(NUU)、数据存储模块、数据重构模块、校验模块和译码输出缓冲模块，如图1所示。其中，控制模块分别产生各子模块的使能，它是译码器的核心控制模块，控制着迭代的正确进行；NUU为译码器的核心运算模块；数据缓冲模块用来判断译码器速率是否大于进入译码器的数据速率；数据存储模块完成中间数据的存储；数据重构模块将变量节点更新的输出数据按照校验节点运算的取数顺序重新排列；校验模块用来校验判决出的码字是否满足校验矩阵。

2.2 节点更新模块（NUU）
    本文实现的译码器采用基于修正因子的分层译码算法，每一层的校验节点处理完成以后，信息立即被用来更新变量节点。它的结果被用来提供给下一层的校验节点处理。因而校验节点处理模块和变量节点处理模块可以合并成同一个模块，简称节点更新模块NUU（Node Update Unit）。
    本文只研究信息位k=1 024的QC-LDPC码，其结构如表1所示。

    图2所示的模块是每层b路并行处理单元中的一个，b为校验矩阵H的循环子矩阵的行数。为了降低部分并行LDPC码译码器中连接的复杂度，节点更新模块(NUU)中节点更新的信息都采用数据串行方法。变量节点的度决定了校验节点单元一次处理的节点数，将校验节点单元处理的节点数设为节点变量的最大值，可以通过逻辑选通来适应不同的码率。

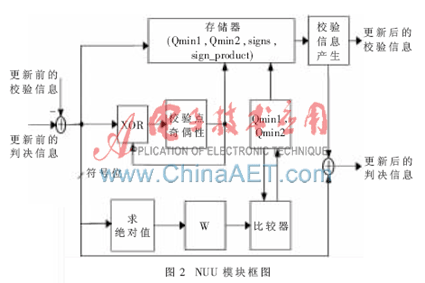
2.3 数据存储模块
      本文对接收到的原始数据和计算过程产生的中间数据都采用了8 bit整数量化，其中1 bit为符号位，7 bit为数据位。将译码开始时外部输入的数据存入判决信息存储器时，将接收的前b个二进制数据的最高位依次级联为一个b bit的数据，存入判决信息存储器1，地址为0；将前b个数据的次高位级联为一个b bit的数据，存入判决信息存储器2；然后依次将b个数据剩下的相同位置的数据级联，存入判决信息存储器2：7，地址为0；将接收的后b个数据按上述同样的方式存入判决信息存储器1：7，地址为1；当待译码字的所有数据都存入了判决信息存储器后，就开始译码。图3为数据存储模块框图。

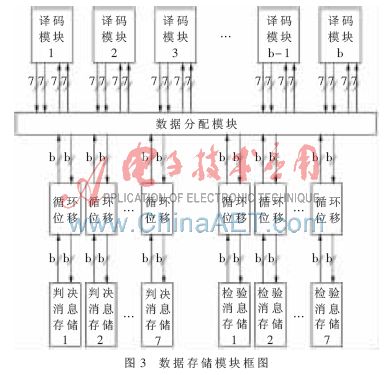
    当开始译码时，再将存放在存储器里的b个级联的数据还原成b个7 bit的数据。而当信息需要传递给下一层时，按照校验节点运算的取数顺序重新排列判决信息在子矩阵中的位置，这个功能由数据重构模块实现。
3 性能测试
3.1 误码率性能测试
    首先由数字信号发生器对待译码字进行BPSK调制，然后由加噪仪对调制后的信号加噪（高斯白噪声）。在信号的接收端对该信号经行解调、同步后，将待译码字的信道软信息输入FPGA译码芯片。译码芯片将译码后的结果传输给误码仪进行误码比对，计算误码率。
    图4为8 bit整数量化译码的仿真结果，在译码过程中所有的数据长度都为8 bit，其中符号位1 bit，信息位7 bit。其中，1/2和2/3码率的QC-LDPC码，迭代的最大次数为25；4/5码率的QC-LDPC码，迭代的最大次数为20。

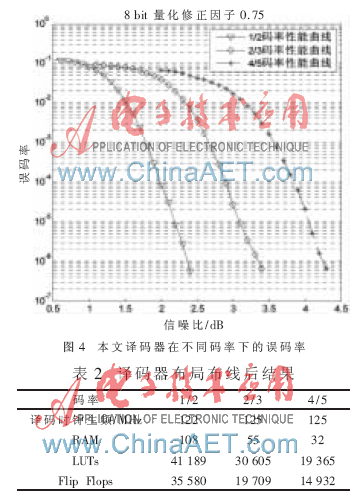
3.2 译码器布局布线后结果
    按照本节的半并行码结构，在Xilinx公司的Virtex4 vlx160芯片上分别实现了CCSDS推荐的三种不同码率的QC-LDPC码编码器。经过综合布线后得到芯片内嵌的存储单元，如表2所示。
3.3 译码速率性能测试
　　输入缓冲模块中的FIFO有溢出指示电平en_full，可用来判断译码速率是否合适。若数据缓冲区没有数据溢出，则逐步增加数字信号发生器的符号速率，一直增加到缓冲区溢出的临界值。这时得到的数字信号发生器的信息比特速率就是该译码器在该信噪比条件下的最大译码速率。
    最后测试结果：当1/2码率QC-LDPC码译码器在信噪比Eb/N0=2 dB时，译码速率为183 Mb/s；当2/3码率QC-LDPC码译码器在信噪比Eb/N0=2.7 dB时，译码速率为143 Mb/s；当4/5码率QC-LDPC码译码器在信噪比Eb/N0=3.6 dB时，译码速率为90 Mb/s。
    随着信噪比的增加，译码器译完一个码字的迭代次数将随之减少，因此译码的速率会随着信噪比的增加而增加，但是并不是完全成比例的增加。这是因为待译码字的输入速率是受限的，随着译码速率的增加，译码器将拥有超过其待译码字输入速率的能力，此时译码的速率将不再增加。本文实现的译码器最高可实现200 Mb/s的译码速率。
    在对CCSDS推荐的QC-LDPC码研究的基础上，设计了一种基于改进分层译码算法的部分并行结构QC-LDPC译码器，并给出了节点更新模块和数据存储模块的结构。译码器性能测试表明，该结构译码速率高，设计模块化，布线简单，便于Xilinx综合布线工具生成性能良好的可下载文件。
参考文献
[1] GALLAGER R G.Low density parity-check codes[J].IEEE Trans.Inf.Theory，1962，8(1)：21-28.
[2] The consultative committee for space data systems.131.1-O-2 low density parity check codes for use in near-earth  and deep space applications[S].Washington D.C，USA，CCSDS，2007.
[3] KSCHISCHANG F R，FREY B J，LOELIGER H A.Factor  graphs and the sum-product algorithm[J].IEEE Transaction.  Information.Theory，2001(47)：498-519.
[4] FREY B J，KSCHISCHANG F R.Probability propagation  and iterative decoding[C].In Proceeding.34th Allerton Conference.On Communication，Control，and Computing，Monticello，Illinois，Oct.1996.
[5] Zhang Luoming，Gui Lin，Xu Youyun，et al.Configurable multi-rate decoder architecture for QC-LDPC codes based  broadband broadcasting system[J].IEEE Transactons on  broadcasting，2008，54(2)：226-235.
[6] GUNNAM K K，CHOI G S，Wang Weihuang，et al. Decoding of quasic-cyclic LDPC codes using an on-the-fly computation[C].Signals，Systems and Computers，2006. ACSSC’06，2006(1)：1192-1199.