随着移动通信的发展，TD-SCDMA智能天线中，下行采用波束形成技术，提高下行信干比，增强覆盖。在3GPP LTE 协议TS 36.213 Release 8中定义了7种下行发射模式，其中模式7为单天线端口（端口5）即为通常所述的波束赋形模式[1]，主要用途是提高SINR、增加小区的覆盖范围。LTE标准支持波束形成技术，该技术是针对基站使用小间距的天线阵列，为用户形成特定指向的波束。

    采样矩阵求逆（SMI）算法是自适应波束形成中常用的方法，它收敛快，干扰抑制效果好。在数值分析中，SMI算法要估计接收信号的自相关矩阵，自相关矩阵的特征值的分散度(条件数) 要大于数据矩阵本身，条件数越大，数值鲁棒性越差，显然任何一种不求自相关矩阵而直接对数据矩阵计算的算法都会得到较SMI好的数值特性[2]。QR分解，它通过对输入数据矩阵做QR分解完成协方差矩阵的估计，进而求得权向量，具有更好的数值特性和固有的高度并行性[3]，因此在实际的各种系统中得到了广泛的应用。但当采样数较少，采样协方差矩阵估计值的噪声特征值分散会导致波束形成算法的性能下降问题。
    针对此缺陷，本文提出了对角加载奇异值（DSVD）分解的算法，该算法首先对采样数据矩阵进行奇异值（SVD）分解，再利用对角加载技术能减弱小特征值对应的噪声波束的影响这一优势，实现对角加载，DSVD算法不仅提高了算法的性能而且降低了复杂度。


3 仿真结果
    仿真条件：假设信号的波达方向为0°，干扰源的波达方向分别为50°（干扰噪声比为30 dB）SNR=20 dB。图1为采样数N=300 QR分解算法和DSVD分解算法的阵列方向图；图2为采样数N=30 QR分解算法和DSVD分解算法的阵列方向图；图3为QR分解算法和DSVD分解算法的阵列输出SINR随采样数的变化曲线；图4为采样数N=20 的QR分解算法、DSVD算法的阵列输出信干噪比SINR随信噪比SNR的变化曲线；图5为采样数N=20 的QR分解算法与DSVD算法的BER比较图。

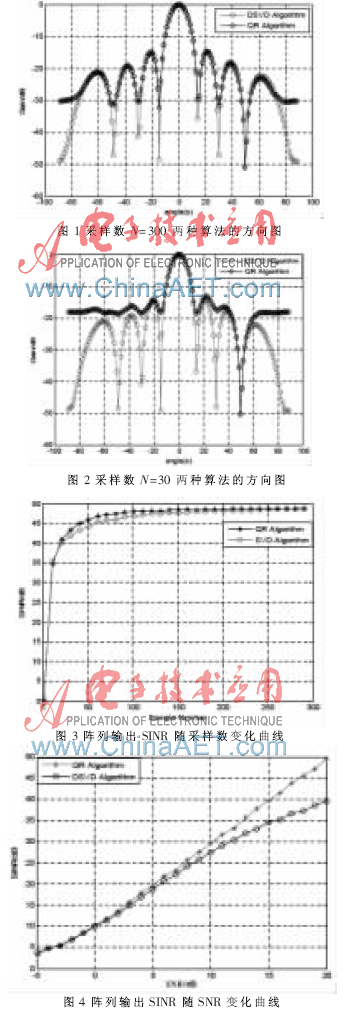
    从图1可以看出，在采样数较大的情况下，两种算法的方向图都在期望信号处形成了很高的增益，达到了提取期望信号的目的，在干扰方向50°上都形成了零陷，抑制了干扰，两种算法形成的零陷一样深。从图2可以看出，在采样数较少的情况下，QR分解算法的旁瓣较高，其性能很不理想，但DSVD算法的旁瓣都较低，对旁瓣性能的改善非常明显。从图3可以看出，文中的QR分解算法和DSVD分解算法都有很高的输出SINR，而且这两种算法的输出SINR接近，对角加载的算法在采样数较少的情况下的就有很好的性能，且其性能优于没有进行对角加载的算法的性能。从图4也可以看出，对角加载SVD算法的输出SINR高于QR算法的SINR。再结合图5，可以得出DSVD算法的性能优于QR算法的性能，可以提高波束形成算法的性能。

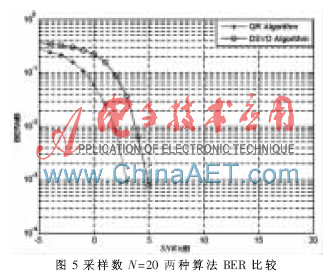
    在自适应波束形成算法中，QR算法优于SMI算法，提高了数据鲁棒性。DSVD分解算法和QR分解算法都有很好的性能，能实现正确的波束形成，提高系统增益。仿真结果证明了在采样数较少的情况下，通过DSVD算法，降低了小特征值及其特征向量的扰动，使DSVD分解算法的性能优于QR分解算法的性能。
参考文献
[1] 曾召华.LTE基本原理与关键技术[M].西安: 西安电子科技大学出版社, 2010.
[2] 张引，黄建国.基于特征结构的可变对角加载波束形成算法[J].电声技术,2008,32(11):61-64.
[3] 倪淑燕，程乃平，倪正中.固定样值数目的QR分解递推算法[J]. 通信学报，2010,31（8A）：195-200.
[4] Yuen Chau, Sun Sumei, Zhang Jiankang.Comparative study  of  QRS in closed-loop beamforming systems[J]. in Proceedings of the IEEE Military Communications Conference, Orlando, FL, Oct. 2007.
[5] CARLSON B D. Covariance matrix estimation errors and diagonal loading in adaptive arrays[J]. IEEE Trans, Aerospace and Electronic Systems, 1988, 24(4)：397-401.