摘   要： 介绍了采用数字图像处理技术对不规则岩石节理裂隙进行宽度测量的不同方法。对比分析了常用的等面积圆算法、等面积椭圆算法和简单Ferret算法的应用缺陷，提出了改进的Ferret算法，详细说明了其实现原理，并通过实例验证了改进的Ferret算法的可行性。
关键词： 图像分析  岩石节理  宽度测量  Ferret算法

　　岩体节理裂隙宽度的测量在地质勘探、矿山工程、公路铁路建设和核电工程等诸多工程领域都有广泛的应用。但是由于裂隙形成原因的多样化，给它的测量与研究带来了极大难度。一种最简单的测量宽度的方法，就是用卡钳(测径仪)来测量节理裂隙二侧岩体断裂面的垂直距离。这种方法受人为因素和仪器精度的影响很大，结果不稳定且数据不精确。而对于岩体微裂隙的测量来说，则只能在显微镜下进行。一般采用的方法是：首先对对象岩体取样，并从中采集数字图像信息，然后沿用传统的人工测量方法，对图像中的目标物体进行测量，最后得出测量结果。这种方法只是在数据采集时提高了精确度，但在测量过程中由于缺少对现有图像分析技术的应用，测量结果并不理想。目前常用的图像分析技术主要是一些图像测量算法，其中有：当量圆直径算法，当量椭圆长、短轴算法等。它们都能对一定条件下的图形进行稳定、精确的测量，但是单独使用一种算法又有局限性。用于节理裂隙等面积的圆形的直径计算裂隙的宽度(当量圆直径算法)，这种方法实现简单但适用范围有限，要求被测对象的边界起伏较大才可以达到满意效果。用于节理裂隙等面积的椭圆的短轴计算裂隙的宽度(简称椭圆算法)，这种方法实现起来十分复杂，但效果较好，实际中仍有应用。此外，简单Ferret算法(也称Ferret Box算法)[1]采用测量与目标物体相切的2条平行线之间距离的方法来确定不规则图形的长、宽等几何特征，但是这种方法由于缺少对测量方向的确定，使得宽度值不稳定，需要进一步改进。
　　本文以简单Ferret算法为基础，介绍其改进算法，并通过对一个岩石节理裂隙的实际测量过程的介绍和测量结果分析，对比了改进的Ferret算法和目前常用的测量算法的优劣。
1  数字图像处理原理及算法
　　在数字图像处理技术中，对不规则二维几何图形的测量多采用多边形近似的方法[2]。对于复杂的不规则二维几何图形来说，通常借用规则的几何图形对它们进行近似计算，从而获得被测目标图形的几何特征值。需要注意的是，在对图像中的目标物体进行测量之前，一般先要对原始图像进行二值化处理[2]，然后再以二值图为基础进行测量分析。
1.1 简单Ferret算法原理
　　简单Ferret算法首先从二值图的边界任选一点，经过此点做图形的切线。取与该切线平行的直线，使它与图形的另外一侧边界相切，当这2条切线间的垂直距离最大时，此时的距离为被测图形的长度值；当垂直距离达到最小时为被测图形的宽度值。用Ferret Box测量不规则图形的宽度示意图如图1所示。图中Fm为最大值。

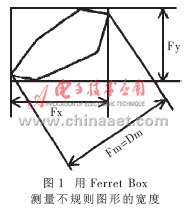
　　可以看出这种算法虽然简单却存在缺陷。原因是：要想找到垂直距离的最大值和最小值，就要进行多次取值和比较，对于边界变化频繁的图形来说操作十分繁琐。而且这种方法对于凸多边形比较适用，对于凹多边形特别像节理裂隙这样边界变化很大的复杂图形来说确定切线存在难度，这将影响测量工作的准确度。下面将以简单Ferret算法为基础，介绍一种比较稳定的测量宽度的算法——改进的Ferret算法。
1.2 改进的Ferret算法原理
　　改进的Ferret算法充分利用了二维几何图形的旋转不变性原理，弥补了简单Ferret算法不易测量凹多边形的缺陷，原理步骤如下。
　　(1)使用求最小二阶矩的方法，惟一确定测量不规则图形宽度的参考方向。
　　(2)以确定的参考方向为基准，再采用Ferret Box的方法获得图形的长度和宽度。
　　可以看出改进的Ferret算法主要是增加了确定方向的方法，它使得宽度的测量结果趋于稳定。
　　采用最小二阶矩的方法确定参考方向如图2所示。图中，虚线为过物体质心的任意一条直线，二值图曲线方程为f(x，y)，点(x，y)到虚线的垂直距离R为转动半径，可得转动惯量方程：

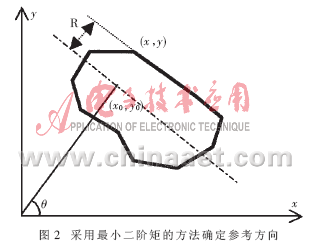
　　根据图2可得：

2  图例应用
2.1 岩石节理图片的采集
　　首先，获取岩石标本。对需要研究的岩体进行钻孔，并向孔中放入放射性物质，经过一个星期的放射过程使放射物充满岩体中可以达到的裂隙。然后，切割岩石。用10～50倍显微镜采集有代表性的节理的原始彩色图像。本例中采集样本使用的放大比例设定为：一个光点代表的实际长度为0.004mm。由于选用了比较大的放大比例，使微节理裂隙的物理特征更加突出，图片规模也随之较大。采集过程中把整条节理裂隙分成34张独立图像分别拍摄，每张图片的大小为760×230个象素点。为简洁起见，文中选取该组图片中的一张进行处理并对各种测量方法和结果进行对比分析。
2.2 图像处理过程
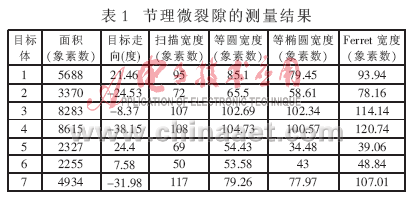
　　首先对采集到的原始彩色图像进行二值化处理， 为便于各种算法的测量比较以及减少偶然性误差，对被分析的图像采取平均分割的方法等分成7份，对分割后的图像使用改进的Ferret算法进行测量。图3和图4为裂隙的原始图和二值化后被分割的图像。此裂隙变化较复杂，起伏较大，裂隙中间有孔洞(或填充物质)，边界有“烟雾”，这些都会影响测量的准确度，因此测量前先采用阈值法去除边界噪声。经过改进的Ferret算法处理后的效果图如图5所示，测量结果统计如表１所示。

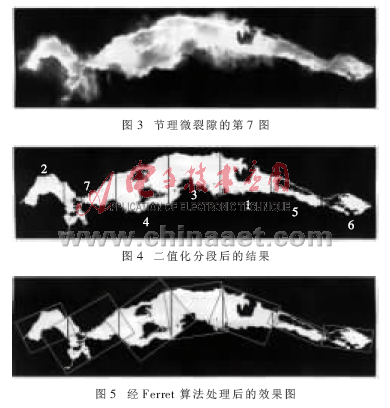
2.3 统计分析
　　由于椭圆算法使用广泛且结果理想，所以以它作为基准进行对比分析。三种算法宽度测量结果的对比如图6所示。由图可知：对于3、4、7这三段的测量，当量圆直径算法和椭圆算法得出的结果比较接近，从图4中也可以看出3、4、7各段裂隙的长宽差值近似。在这种情况下Ferret算法并不能表现出很好的优越性；而对于5、6段的测量，椭圆算法和Ferret算法的结果比较接近，但5、6二段的长宽差很大，可见对于长宽差比较大的不规则图形可以使用Ferret算法测量。这就要求使用Ferret算法进行实际测量时，要注意测量前的分割尺度，使长宽有一定的差距，使用Ferret算法才可以达到理想的效果。
　　经过大量宽度测量的实验对比表明：Ferret算法在测量不规则图形，特别是那些长宽差比较大的图形都得到了理想效果。
3  总  结
　　大量的数字图像处理技术应用在工程测量方面，由于其各异性，面对众多测量算法，要选用某种适合的算法，需要做大量的对比研究。对于规则的被测图形来说，当量圆算法和当量椭圆算法基本可以满足需求，而Ferret算法在大量长宽差比较大的不规则图形测量方面表现出良好的适应性，而且达到了满意的效果。本文分析了简单Ferret算法的原理，提出了改进的Ferret算法，给出了一个基于改进的Ferret算法的岩石节理宽度测量的实例过程。然而，在实际测量中，分割图像时选取的长度大小、非实裂隙的中间孔洞以及边界噪声等都会对宽度测量产生一定的影响，这些都将是今后要解决的问题。
参考文献
1   Mora C F，Kwan A K，Chan  H C.Particle Size Distribution  Analysis of Coarse Aggregate Using Digital Image Processing.Cement and Concrete Research，1998；28(6)
2   Gonzalez R C著，阮秋琦，阮宇智译.数字图像处理(第二 版).北京：电子工业出版社，2002
3   Ito A，Aoki Y，Hashirnoto S.Accurate Extraction and  Measurement of Fine Cracks from Concrete Block Surface  Image.In：IECON 02，IEEE 2002 28th Annual Conference of the Industrial Electronics Society，2002
4   Guimaraes L V，Suzim A A，Maeda J.A New Automatic  Circular Decomposition Algorithm Applied to Blood Cells   Image.In：Proceedings of IEEE International Symposium   on Bio-Informatics and Biomedical Engineering，Arlington， VA，USA，New York，2000