开关电源电压输入回路的滤波电感，其分布电容的大小对EMC指标的影响非常大，因此也需要对滤波电感线圈的分布电容构成以及原理有充分的理解。从原理上来说，滤波电感线圈的分布电容与开关变压器线圈的分布电容基本上是没有根本区别的；因此，对分布电容的分析与计算方法，对滤波电感线圈同样有效。

    开关变压器初、次级线圈的分布电容，对开关电源性能指标的影响也很重要，它会与变压器线圈的漏感组成振荡回路产生振荡。当输入脉冲电压的上升或下降率大于振荡波形的上升或下降率的时候，振荡回路就吸收能量，使输入脉冲波形的前、后沿都变差；而当输入脉冲电压的上升或下降率小于振荡波形的上升或下降率的时候，振荡回路就会释放能量，使电路产生振荡。如果振荡回路的品质因数比较高，电路就会产生寄生振荡，并产生EMI干扰。

    另外，开关电源电压输入回路的滤波电感，其分布电容的大小对EMC指标的影响非常大，因此在这里也需要对滤波电感线圈的分布电容构成以及原理有充分的理解。从原理上来说，滤波电感线圈的分布电容与开关变压器线圈的分布电容基本上是没有根本区别的，因此，对变压器线圈分布电容的分析与计算方法，对滤波电感线圈同样有效。

    开关变压器初、次级线圈的分布电容与结构有关，因此，要精确计算不同结构的开关变压器初、次级线圈的分布电容难度比较大。下面我们先以最简单的双层线圈结构的开关变压器为例，计算它们的初级或次级线圈的分布电容。

    图2-41是分析计算开关变压器线圈之间分布电容的原理图。

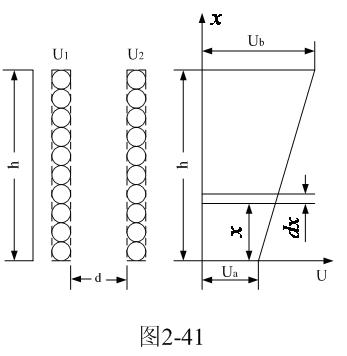
    设圆柱形两层线圈之间的距离为d，高度为h，平均周长为g 。假定两层线圈之间沿高度的电位差为线性变化，即：



    设两个线圈相对应的两表层间的电场近似均匀分布，即近似平板电容器的电场，那么，根据（2-112）式就可以求得该电场贮存的能量为：

    由此可以求得变压器初级或次级两层线圈之间分布电容的表达式：

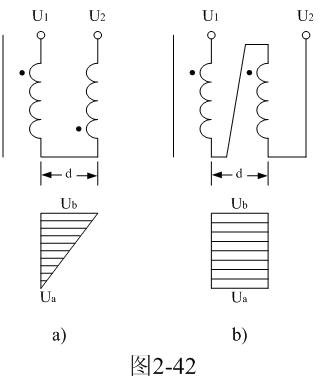
    对于图2-42-b，可求得变压器初级或次级两层线圈之间的分布电容为：

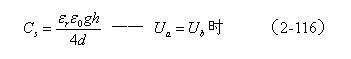
    由此可知，变压器初级或次级两层线圈之间的分布电容，除了与变压器线圈的高度、周长、两层线圈之间的距离等参数相关外，还与两层线圈之间的电位差有关。

    为了更好地对多层线圈的分布电容进一步进行分析，我们把（2-114）式改写成一个静态电容与一个动态系数相乘的形式，即：

    当变压器的线圈为多层时，我们只需反复利用（2-117）式来对相邻两层之间的分布电容独立进行计算，然后把结果相加即可。如果一定要写出计算多层线圈分布电容的表达式，则变压器多层线圈的分布电容可表示为：





    由此可以知道，变压器线圈的总分布电容的大小主要与线圈的层数（n-1）成正比，与层间的距离d成反比，并且与变压器线圈的连接方法还有关。

    因此，我们不能把各层之间的分布电容当成普通电容的概念来理解。普通电容互相串联时，总电容的容量，总是小于其中任意一个电容的容量；而变压器线圈的层间分布电容看起来是属于串联，但其结果是越串连越大。这是为什么呢？这是因为变压器线圈层间分布电容的电压主要不是靠串联回路来充电的，而是靠线圈之间互相感应产生的。
 
    不但如此，变压器次级线圈的分布电容同样也要感应到初级线圈来。大多数场合，在考虑变压器线圈总的分布电容的时候，一般都需要把初、次级线圈的分布电容一起来考虑。例如，电视机的高压包，其次级线圈绕组的分布电容一般都很大，折算到初级线圈后，初级线圈总的分布电容就更大，一般可达好几千微微法，如不采取分段绕线措施，最大可达好几万微微法。



    直接对变压器线圈的总分布电容进行测试是有些困难的，但可以测试每层线圈之间的静态电容，方法是要把图2-42中线圈层与层之间的连线断开；然后把测量结果乘以一个动态系数，即得到本层的分布电容，最后把各层的分布电容全部相加即可得到总分布电容。

    如果不考虑变压器次级线圈对初级线圈的影响，对于一个功率大约为100瓦的开关变压器，其初级线圈的分布电容大约在100~2000微微法之间；如果把次级线圈的分别电容也考虑进去，总的分布电容可能要大一倍左右。因此，分布电容对输出波形的影响也是很大的。

    为了减少变压器线圈的分布电容，特别是EMC滤波器线圈的分布电容，最好不要把线圈分成多层叠绕，而是把线圈分段来绕，这样可以降低（2-119）式或（2-120）式中每层线圈的高度h，从而可以减小线圈总的分布电容。