1 引 言
机械故障诊断中由传感器检测到的信号往往十分复杂,且信号中的奇异部分常载有机械设备运行状态特征的重要信息。因此判断状态信号的奇异点出现时刻,并对信号奇异性实现定量描述,在机械故障诊断信号分析和处理中有着非常重要的意义。
信号的奇异性分析是提取信号特征的重要手段,傅里叶变换一直是研究信号奇异性的经典工具,但是由于傅里叶变换只能确定信号的整体信息,难以刻画信号的局部奇异性,而小波分析理论能实现信号的时-频局部化描述,为信号奇异性分析提供有了力的工具。利用小波奇异性检测理论,本文提出了一一种根据奇异点的局部奇异性信息来诊断机械故障的新方法。
2 信号奇异性
数学上称无限次可导函数是光滑的或没有奇异性的,若函数在某处有间断或某阶导数不连续,则称函数在此处有奇异性,该点就是奇异点。奇异性反映了信号的不规则程度,信号的奇异性由Lipschitz指数来描述和衡量。
设n为非负整数,n≤α≤n+1,如果存在两个常数A和h0(>0),及n次多项式Pn(t),使得对任意的t0,均有:
![]()
则称f(t)在点t0处具有Lipschitz指数α。
由此可以看出,Lipschitz指数刻画了函数f(t)在点t0的奇异性。Lipschitz指数α越大,则函数f(t)越光滑。如果函数f(t)在点t0连续、可微,那么Lipschitz指数α=1;如果在点t0不连续,但有界,则Lipschitz指数α=0,当Lipschitz指数α<1时,函数f(t)在点t0是奇异的。
3 小波变换与信号奇异性
小波变换是将信号与一个时域和频域均具有局部化性质的平移伸缩小波基函数进行卷积,将信号分解成位于不同频带时段上的各个成分。
若基本小波函数Ψ(τ)∈L2(R),且满足容许性条件:
![]()
则函数(信号)f(t)∈L2(R)在尺度s和位置t的小波变换定义为:
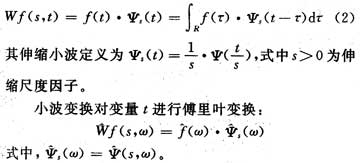
由小波变换的特征可知,小波变换Wf(s,t0)的值强烈依赖于信号f(t)在点t0处领域附近的值,并且尺度s越小,领域问也越小,因此在合适的尺度上,Wf(s,t0)将提供所需要的信号在点t0附近的局部信息。下面的定理给出了信号小波变换沿尺度的衰减与信号局部Lipschitz指数的关系,并由此得到信号奇异性的特征。

定理1 设f(t)∈L2(R),Ψ(t)为基本小波。则f(t)在某开区间上为Lipschitz指数α的充要条件是:
![]()
由定理1可以看出当s→0时,∣f(s,t)∣衰减的快慢。如果将尺度理解为频率的倒数,则式(3)给出的Lipschitz α是对信号在区间内奇异性的局部刻画,而不仅仅是全部实数域上的整体刻画。
信号的奇异性在小波变换下的特征由定理2描述,但是如何从信号小波变换来确定信号的奇异性?研究发现,信号的奇异点与小波变换模极大值与该点Lipschitz指数有密切的关系。在尺度s下,若d/dtWf(s,t)在t0处有一过零点,则t0是小波变换的局部极值点,若在某一领域δt0,∨t∈δt0,∣Wf(s,t)∣≤∣Wf(s,t0)∣,则t0掬小渡变换的模极值。若∨(s,tΓ)∈Γ,tΓ是在尺度s下的小渡变换的模极大值点,则称{(s,tΓ∣s>0)}中的某一条曲线Γ为小波变换极值链。
定理2 设n为正数,Ψ(t)是具有紧支集的小波函数,有n阶消失矩而且n阶连续可微。那么,如果有尺度s
定理2 说明如果小波变换无局部最大值,在该区间信号非奇异。由此进一步可以推论,f(t)非Lipschitzn的点t的闭包,包含在f(t)的小波变换模极值点的闭包之内,说明f(t)的所有奇异点均可沿小波变换极值链定位,实际应用中便是用考查小波变换的模极值点得到信号奇异点。从奇异信号在小波变换下的特征分析,可以有这样的结论:信号小渡变换模极值点即是信号的奇异点,而描述信号奇异性Lipschitz指数是由沿小波变换尺度的衰减计算。这对信号分析、特征提取等均有重要的应用价值。
4 信号奇异性检测
当小波函数可看作某一平滑函数的一阶导数时,信号小波变换模的局部极值点对应予信号的突变点;当小波函数可看作巢一平滑蕊数的二阶导数时,信号小波变换的过零点对应于信号的突变点。因此,采用小波变换模的过零点和局部极值点的方法可以检测信号的突变点。比较来说,用局部极值点的方法进行检测更具优越性。
一般信号奇异性分为两种情况:
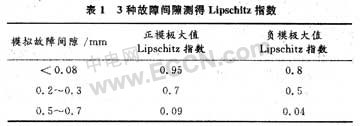
(1)信号在某一时刻其幅值发生突变,引起信号的不连续,这种类型的突变称为第一种类型的间断点(见图1);
(2)信号外观上很光滑,幅值没有发生突变,但是信号的一阶微分有突变发生且一阶不连续,这种类型的突变称为第二种类型的间断点(见图2)。
应用小波分析可以检测出信号中突变点的位置、类型以及变化的幅度,下面分别对这两类间断点进行检测。
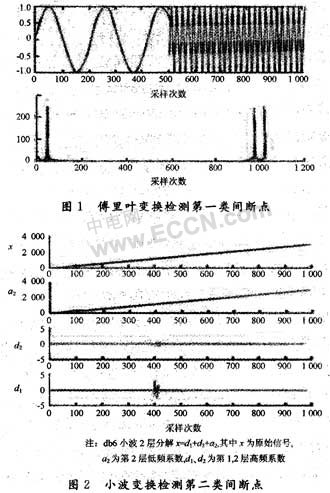
图1中信号的不连续是由予低频特征的正弦信号在后半部分突然有高频特征的正弦信号加入,首先利用傅里叶变换对信号在频城进行分析,发现无法检测信号的间断点,这是由于傅里叶变换不具有时间分辨力。接着利用小波分析进行分析,如图3所示,使用db6小渡将信号进行6层分解,以检测第一种类型的间断点,可以非常清楚地观察到信号的不连续点,即高频特征的正弦信号的加入点,这是因为间断点包含了高频信息。如果只需要识别检测第一种类型的间断点,可以非常清楚地观察到信号的不连续点,即高频特征的正弦信号的加入点,这是因为间断点包含了商频信息。如果只需要识别信号的不连续点,用dbl小波比db6小波效果要好。
以上检测实例表明小波分析在检测信号的奇异点时具有傅里叶变换无法比拟的优越性,利用小波分析可以精确地检测出信号的突变点。即高频特征的正弦信号的加入点,这是因为间断点包含了高频信息。而如果只需要识别信号的不连续点,用dbl小波比db6小波效果要好。
图2中,原始信号是由两个独立的满足指数方程的信号在t=400处连接起来的。因此它看上去是光滑的,但它的一阶微分有突变。采用db6小波对信号分解后,在信号的第一层高频系数d1中可以明显地看到t=100的间断点。要注意的是,在信号奇异点的检测中,选择小波的正则性(正则性一般甩来刻画函数的光滑程度,正则性越高,函数的光滑性越好)非常重要,因为这时小波可实现一个长的冲激响应滤波器。
5 故障诊断实例分析
小波变换在故障诊断中的应用十分广泛,如奇异信号检测、信噪分离和频带分析等。本文采用奇异指数德量来实现信号的奇异性检测,从而实现故障诊断。信号奇异性指数的大小直接反映了故障的程度。故障的发生往往引起时域波形的波峰突变,因此,通过奇异性指数提取和统计,可作为信号时域的特征因子,以实现故障的自动诊断。
5.1 试验方案
试验对象是某齿轮减速箱的406滚动轴承,试验通过研磨滚动轴承内圈来模拟轴承内圈的磨损故障,以不同的配合间隙模拟故障的严重程度。测试转速1 480 r/min,采样频率确定10 kHz是完全能够满足测试要求的,整个试验在减速箱试验台架上进行,信号采集系统框图如图4所示。
5.2 试验信号的处理与分析
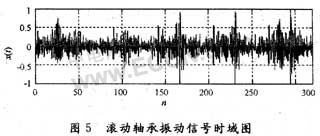
模拟故障间隙0.2~0.3 mm,提取一个周期内的时域振动信号如图5所示。
由试验可得出以下结论:
(1)由滚动轴承内圈磨损引起的故障在振动信号中体现为奇异的冲击波形,通过基于小波变换的信号奇异性检测可以有效定位该故障波形,从而检测出故障。
(2)根据理论分析,若磨损越严重,则冲击越大,波形越陡,表征信号波形奇异性Lipschitz指数越小;通过试验,验证了Lipschitz指数可以表征故障严重程度,为故障严重的判别提供了依据。
6 结语
信号奇异点可通过信号的小波变换局部极大值来定位,而奇异性运用该点的Lipschitz指数a来定量描述,运用该理论来实现机械故障信号的奇异性检测,比常规手段更优越。本文通过实例说明,若将该方法应用到机械设备故障的诊断中,快速实现故障的正确诊断,对于提高机械设备工作的稳定性具有十分重要的意义。
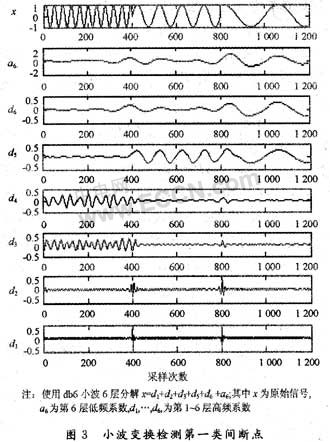

在试验中故障信号是奇异的,其Lipschitz指数小于1,因此Haar小波可满足检测的要求,并且使小波变换的模极大值最小。试验分别模拟了3种故障间隙,测得Lipschitz指数如表1所示。