摘 要: 对传统的K-平均算法作了简单的介绍和讨论,提出了一种具有单纯型法思想的K-中心点轮换法。分别对比了K-均值算法与K-中心点轮换算法的时间复杂度,针对K-中心点轮换算法的时间复杂度提出了一种基于抽样原理的改进算法,并对K-中心点轮换算法聚类数目的选择进行了各种改进方法的探索。同时,基于主流的weka开源数据挖掘工具实现了改进算法。实验结果表明了算法的有效性。
关键词: K-均值;K-中心点轮换;抽样;聚类数目;weka
作为统计学的一个分支,聚类分析已经被研究了许多年[1-5],但主要集中在基于距离的聚类分析上。在机器学习领域,聚类是无指导学习的一个例子。与分类不同,聚类不依赖于预先定义的类和带标号的训练实例,可见,聚类是观察式学习,而不是示例式学习[1]。在概念聚类中,一组点只有当它们可以被一个概念描述时才形成一个簇。这不同于基于几何距离来度量相似度的传统聚类。目前在文献中存在着大量的聚类算法,算法的选择取决于数据集的类型、聚类的目的和应用。如果聚类分析被用作描述或探查的工具,可以对同样的数据集尝试多种算法,以发现数据集可能揭示的结果。
1 基于划分的聚类分析算法及改进
聚类分析,一般认为就是试图发现数据点集中内在的结构,使同一簇内的数据点相似度高,不同簇之间的数据点相异度高[3]。由于相似度、相异度的定义往往根据具体情况而定,而且什么是最好的聚类结果,往往也与具体问题、具体要求有关。将聚类问题转化为一种优化问题,再通过数学规划的方法来进行求解是研究聚类分析的一个重要方向。
给定n个对象或者数据元组的数据库,应用划分方法构建数据的k个划分,每个划分表示一簇,k≤n。也就是说,将数据划分为k组,并满足如下要求:(1)每一组至少包含一个对象;(2)每个对象必须只属于一组。
给定要构建的划分数目k,应用划分方法创建一个初始划分。然后采用迭代重定位技术,尝试通过对象在组间移动来改进划分。
设在m维欧氏空间中有n个点,在这个空间中的某个范围内选取k个中心位置mi(i=1,2,…,k),使得这n个点到各自最近的中心位置的距离平方之和最小。这是最初的一种优化目标函数。
1.1 传统的K-均值算法[1]
K-均值算法(K-means)是最基本的聚类分析算法,以k为参数,把n个对象分为k个簇,以使簇内具有较高的相似度,而簇间的相似度较低。相似度的计算根据一个簇中点的平均值(被看作簇的重心)来进行。K-means聚类算法的描述和处理流程[1-2]如下:
K-means是用于划分的K-均值算法,每个簇的中点用簇中对象的均值表示。其输入为簇的数目k和包含n个对象的数据集,输出为k个簇的集合。
算法流程:
(1)从D中随机选择k个对象,每个对象初始地代表一个簇的平均值或质心;
(2)repeat;
(3)根据簇中对象的均值,将每个对象(重新)指派给最相似的簇;
(4)更新每个簇的平均值,即计算每个簇中点的均值;
(5)直到准则函数收敛。

1.2 K-means算法的不足
K-means算法有以下不足:(1)算法对初始值的选取依赖性极大。初始值不同,往往得到不同的局部极小值。(2)由于将均值点作为聚类中心进行新一轮计算,远离数据密集区的孤立点和噪声点会导致聚类中心偏离真正的数据密集区,所以K-均值算法对噪声点和孤立点很敏感。
1.3 K-中心点轮换算法
K-平均算法在计算簇内平均值时很容易被“噪声”和孤立点所影响。为了改进这个缺点,可以采用用簇中位置最中心的点(中心点)来取代K-平均算法中簇中点的平均值。这种划分方法仍然是基于最小化所有点与其参照点之间的相异度(如常采用欧氏距离来度量)之和的原则来执行的。
K-中心点轮换算法(K-mediods)是以k为输入参数,试图以穷举的方式重复地使用目标函数值更小的对象来代替当前的中心点,从而将n个对象分为k个簇。具体的算法过程描述如下:对基于中心点的划分的一种K-中心点变种算法,其输入为结果簇的数目k、包含n个对象的数据集;输出为k个簇,使得所有对象与其最近中心点的偏差准则函数最小。
K-mediods算法流程如下:
(1)随机选择k个对象,每个对象初始地代表了一个簇的中心点,这k个对象就组成了当前的中心点集;
(2)repeat;
(3)将每个对象(重新)指派给离它最近的中心点所代表的簇,按照式(1)计算当前的目标函数值;
(4)对n个对象中的每一个对象Oj(j=1,2,…,n)依次执行下面的过程:试图用当前对象Oj去依次替换现有的k个中心点中的每一个中心点mi(i=1,2,…,k),并计算试图替换后的目标函数值,最终选择替换后能获得目标函数值最小的那个中心点进行替换。如果这k个待替换的中心点所对应的目标函数值比当前的目标函数值还要大,则不进行替换;
(5)直到不发生变化;
(6)最终得到一个中心点集,根据这个集合,按照最近邻原则分配所有对象到它所归属的簇中,得到的k个簇就是所有对象的一个局部优化聚类结果。
1.4 算法对比分析
1.4.1 K-means算法性能
K-均值算法在步骤(3)和步骤(4)之间交互迭代,每一步都使目标函数逐步下降,从而产生一个使目标函数值逐步减小的迭代序列,它尝试找出使目标函数值取得最小的一个k划分,但通常只能获得一个局部优化结果。算法的复杂度是O(nkt),其中,n是所有点的数目,k是簇的数目,t是迭代的次数。
1.4.2 K-mediods算法性能
从算法的过程描述,可以看出该算法是一种单纯型思想的算法,它以牺牲时间复杂度来获取更好的聚类效果,下面简单分析一下该算法的时间复杂度。
该算法由于要用到所有对象的距离度量矩阵,其时间复杂度是O(n2)。算法步骤(3)中将n个对象赋给k个中心点所代表的簇,需要时间复杂度为O(nk);计算目标函数值需要时间复杂度为O(n);算法步骤(4)中在每一次试图替换中心点后都需要重新将所有点赋给新的中心点所代表的簇并计算新的目标函数值以供比较,所以这一步的时间复杂度是O(n2k2)。
1.4.3 K-mediods算法优缺点
K-中心点轮换算法是一种使目标函数下降最快的方法,它属于启发式搜索算法,能从n个对象中找出以k个中心点为代表的一个局部优化划分聚类。与K-均值算法比较,K-中心点轮换算法解决了K-均值算法本身的缺陷:
(1)解决了K-均值算法对初始值选择依赖度大的问题。K-均值算法对于不同的初始值,结果往往得到不同的局部极小值。而K-中心点轮换算法采用轮换替换的方法替换中心点,从而与初始值的选择没有关系。
(2)解决了K-均值算法对噪声和离群点的敏感性问题。由于该算法不使用平均值来更改中心点而是选用位置最靠近中心的对象作为中心代表点,因此并不容易受极端数据的影响,具有很好的鲁棒性。
K-中心点轮换算法也存有以下缺点:
(1)由于K-中心点轮换算法是基于划分的一种聚类算法,仍然要求输入要得到的簇的数目k,所以当k的取值不正确时,对聚类的结果影响甚大。
(2)从以上的时间复杂度也可以看出,当n和k较大时,计算代价很高,所以将该算法应用于大数据集时不是很理想。
1.5 K-means与K-mediods对比测试结果与分析
本次测试采用weka Iris数据集对比K-均值算法与K-中心点轮换算法对初始值的依赖性,对比结果如表1所示。通过改变初始随机数种子,使初始值产生变化。

从表2可以看出,对于同一个数据集,K-mediods算法比K-means算法的聚类平均错误率低。
2 K-mediods算法的改进方向
针对K-中心点轮换算法的不足,可以从以下两个方面对其加以改进。
2.1 基于抽样的K-mediods算法
K-中心点轮换算法对小数据集非常有效,但对大数据集没有良好的可伸缩性。为了处理较大的数据集,可以采用基于抽样的方法,即不考虑整个数据集合,而是选择实际数据的一小部分作为数据的代表。在抽样过程中,抽样算法尽可能保证数据不失真,又能体现数据的原始分布特征(如图1所示),然后对抽样数据集使用K-中心点轮换算法。当然基于抽样的算法的有效性取决于抽样数据集与原数据集的相似度。在实际使用中,可以抽取原始数据集D的多个样本,然后对每一个样本Di进行K-中心点轮换算法,从中选择目标准则函数E最小的结果作为输出。
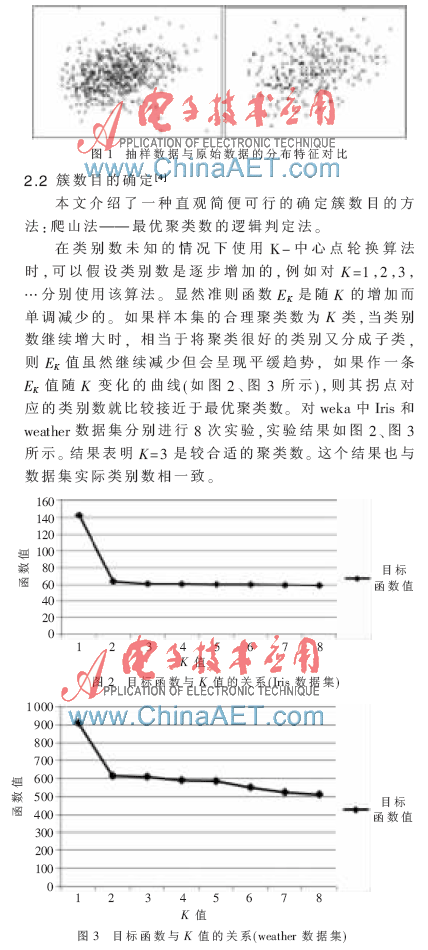
从采用K-中心点轮换算法对同一数据文件的聚类结果可以看到,最终目标函数值与聚类数目K大致满足一个规律:合适的聚类数目往往就在平均最终目标函数值与聚类数目K所形成的关系折线的拐角位置。因为这个目标函数在距离空间中取的是所有点到其最近的中心点的距离的总和,一种极端情况是每个点都是中心点,聚类数目等于所有点数目,显然目标函数的值是0。从直观上可以推测,聚类数目越大,目标函数值就越小,而最终目标函数值的下降由快到慢的那个转折位置往往就是一个关键位置。
通过对K-中心点轮换算法进行抽样改进,成功地解决了K-中心点轮换算法时间复杂度问题,使其能够处理大数据集的聚类分析问题。同时,拐点法是通过实践总结出的一套简单有效的判断最优聚类数的方法。实验表明,该方法简单可行,计算量小,同时不影响现有的算法结构。通过上述两个改进措施,使K-中心点轮换算法真正拥有更好的实际应用价值。
参考文献
[1] HAN J W,KAMBER M.数据挖掘概念与技术[M].范明,孟小峰,译.北京:机械工业出版社,2004:119-124,188-196.
[2] 郑人杰,殷人昆,陶永雷.实用软件工程[M].北京:清华大学出版社,1999:51-53.
[3] JAIN A K,DUBES R C.Algorithms for clustering data[M]. NJ,USA:Prentice-Hall,Inc.,1988.
[4] 周世兵,徐振源,唐旭清.新的K-均值算法最佳聚类数确定方法[J].计算机工程与应用,2010,46(16):27-31.
[5] KAUFMAN L,ROUSSEEUW P J.Finding groups in data:an introduction to cluster analysis[M].New York:John Wiley & Sons,1990.

