摘 要: 本文运用网格环境下的并行计算模型G-PRAM来研究二叉树的后序遍历问题,提出了二叉树后序遍历的一种并行算法,并给出示例和说明。
关键词: 网格环境 二叉树 后序遍历 并行算法
二叉树[1]是一种重要的数据结构,它是n(n≥0)个结点的有限集。它或者是空集(n=0),或者由一个根结点和两棵互不相交的分别称为这个根的左、右子树的二叉树组成。二叉树的遍历可以分为三种:一种是先序遍历,即先访问二叉树的根结点,然后先序遍历左子树,最后先序遍历右子树;第二种是中序遍历,即先中序遍历左子树,再访问二叉树的根结点,最后中序遍历右子树;第三种是后序遍历,即先后序遍历左子树,再后序遍历右子树,最后访问二叉树的根结点。最常见的实现按照遍历过程访问结点,让每个结点被访问且仅被访问一次,这种方式称为串行算法。但是,可以换个角度来研究二叉树的遍历问题,即从串行算法中以二叉树的结点为重点考察对象转变为重点研究二叉树的边的遍历问题[2][4]。当进行二叉树的一次遍历时实际也遍历了二叉树的所有边,而且每条边遍历了两次。一次是从双亲结点到子结点,另一次则是从子结点到双亲结点。如果将每条边变成两条有向边,一条有向边对应向下的遍历,另一条有向边对应向上的遍历,则遍历二叉树的结点问题变成了一个遍历二叉树的边的问题。
因为网格环境具有一般的并行环境所不具有的强处理能力,所以可以给每条边分配一个独立的处理单元(单处理器的网格节点或者多处理器网格节点的一个处理器)进行处理,利用多个处理单元同时对所有的边进行处理,从而并行实现网格环境下的二叉树后序遍历。
1 网格环境下的G-PRAM模型
由Fortune和Wyllie形式化的PRAM[5]模型是一个理想化的并行计算模型,被广泛用来评估并行算法的理论性能。PRAM的思想是假设一个共享存储多处理机系统是由一个具有无限存储容量的共享存储器以及可对它进行访问的许多处理机所组成的系统。并行算法的设计者可以把处理器的能力看成是无限的。一个PRAM由一个控制单元、全局内存和一组处理器集合组成。每个处理器有其自己的私有内存,所有处理器执行相同的指令,但每个处理器处理的数据不同。PRAM模型有四种,不同之处主要在于它们处理读写冲突的方式有差异,包括:互斥读互斥写(Exclusive Read,Exclusive Write,EREW PRAM),并行读互斥写(Concurrent Read,Exclusive Write,CREW PRAM),互斥读并行写(Exclusive Read,Concurrent Write,ERCW PRAM),并行读并行写(Concurrent Read,Concurrent Write,CRCW PRAM)。网格环境往往由相当多的网格结点组成,这些结点有的是多处理器的高性能计算结点,有的是高容量的数据结点,并且往往有一个性能不错且容量也很大的控制结点。因此提出相应的G-PRAM模型。G-PRAM可以看作是一般PRAM的现实化。
定义1 一个G-PRAM由网格环境下的一个控制结点、一个全局数据结点和一组计算结点集合组成。每个网格计算结点有其自己的私有内存,所有网格计算结点的各个处理器执行相同的指令,但每个处理器处理的数据不一样。相应的G-PRAM也有4种方式:EREW G-PRAM、CREW G-PRAM、ERCW G-PRAM、CRCW G-PRAM。
2 并行实现二叉树的后序遍历
2.1 算法过程说明
这里的算法采用并行读互斥写(CREW G-PRAM),算法在实现中对每个二叉树结点保存结点的双亲、左孩子和右孩子,利用这三个参数来描述一个二叉树结点在二叉树中的相对位置。
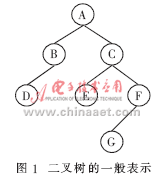
对于如图1所示的二叉树,其数据结构描述如表1所示。
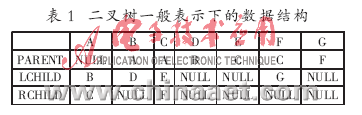
下面分析本文中的算法步骤。
2.1.1 改造二叉树并构造单链表
首先可以将二叉树改造成一个对应的有向图。方法是将二叉树的每条无向边改成一条向下和另一条向上的有向边,结点不变。如图1的二叉树可以改造成如图2的有向图。

根据改造后的有向图构造单链表的过程就是在该有向图中寻找后继边的过程,按照后序遍历的思想,所有的处理器同时处理分配给它的一条边的后继边的问题,最终得到由全部有向边构成的一个单链表。单链表的每个元素对应于改造后的有向图中的一条有向边。
设分配给处理器P[(i,j)]处理的有向边是(i,j),即该边从结点i指向j,则寻找有向边(i,j)后继边的问题可以根据有向边(i,j)的不同类型分别处理。
(1)PARENT(i)=j,说明边(i,j)是一条向上边,即从一个结点指向它的双亲结点。从数据结构的概念中可以得到以下结论,一条向上的边(i,j)在二叉树中的相对位置可以有三种情况:①结点j有右孩子结点,如图3(a)所示。则根据后序遍历的思想可得边(i,j)的后继边是从结点j指向结点j的右孩子结点构成的边;②结点i没有右兄弟结点,而结点j有双亲结点,如图3(b)所示。若根据后序遍历的思想可得边(i,j)的后继边是从结点j指向结点j的双亲结点(parent)构成的边;③结点i既没有兄弟结点,同时也没有双亲结点,如图3(c)所示,说明已经回到了根结点处,边(i,j)没有后继边。但为了方便起见,假设存在一条后继边,从结点j到它自身。

(2)PARENT(i)≠j,也就是边(i,j)是从双亲结点到它的孩子的向下的边。
同理,从数据结构的概念中可以得出这样的结论,即一条向下的边(i,j)在二叉树中的位置可以有如下情况:①结点j有左孩子结点(不管有无右孩子结点),如图4(a)所示。根据后序遍历的思想可知,边(i,j)的后继边是从结点j指向结点j的左孩子结点构成的边。②结点j没有左孩子,但有右孩子,如图4(b)所示。根据后序遍历的思想可得,边(i,j)的后继边是从结点j指向结点j的右孩子结点构成的边。③结点j没有孩子结点,即结点j是叶子结点,如图4(c)所示。则根据后序遍历的思想可得,边(i,j)的后继边是结点j指向结点i的向上边。

2.1.2 给单链表中的每个元素赋权值0或1
此过程也是所有的处理器同时对分配给它的一个元素赋权值(前面构造的单链表中的元素)。根据后序遍历的思想,对于二叉树的一个结点i(根结点例外,必须作不同处理),如果一条向下遍历的边(i,j)从结点i出发,则说明正在寻找从该结点i出发的后继边,结点i没有被访问;如果一条向上遍历的边(i,j)从结点i出发,则说明刚访问完结点i。将单链表中对应向上边的元素赋权值1(表示遍历向上边时增加了一个被访问结点),对应向下边的元素赋权值0(表示遍历向下边时未增加被访问结点),对应根结点的环形边元素也赋权值0(特殊处理)。
2.1.3 计算单链表中各元素的位序
单链表中每个元素需要分配一个处理器去计算其位序。一棵有N个结点的二叉树具有(N-1)条无向边。由于我们将每条无向边转换成一条向上边和一条向下边,所以它共有2(N-1)条边,这意味着单链表中有2(N-1)个元素。所以,需要2(N-1)个处理器来计算单链表中元素的位序。利用计算单链表位序的后缀和算法可以算出单链表中每个元素的位序[6]。
2.1.4 求权值为1的元素的相应结点的遍历顺序号
由于权值为1(向上的边)的元素所代表的边都是向上的边(不妨设该边为(i,j)),即结点i在边(i,j)遍历时被访问,而结点j还未被访问。因此,用单链表中权值为1的元素的位序表示它所代表的边(i,j)中结点i的位序,从而可以得到二叉树中全部结点的位序。结点的位序是结点被访问的先后顺序的逆序。只要用结点个数N减去每个结点的位序就可以得到每个结点的后序遍历顺序号。与前几步一样,这里也是一个处理器计算一个结点的顺序号,多个处理器并行工作,最后,得到一棵二叉树的后序遍历的结点顺序。
2.2 算法示意代码
算法描述如下:
int n; //二叉树的结点个数
int parent[n]; //父结点数组
int lchild[n]; //左孩子结点数组
int rchild[n]; //右孩子结点数组
int succ[(n,n)]; //后继边数组
int position[(n,n)]; //链表元素的位序数组
int postnode[n]; //结点顺序号数组
PostOrder(bitree *t)
//P[(i,j)]是处理对应边(i,j)的一个处理器,共2(n-1)个
{
forall P[(i,j)] do //构造单链表
{
if(lchild[j]==i)
{ if(rchild[j]!=null)
succ[(i,j)]=(j,j.rchild);
else if(parent[j]!=null)
succ[(i,j)]=(j,,j.parent);
else{
succ[(i,j)]=(j,j);
postnode[j]=0;//j是根结点
}//else
}//if
else if(rchild[j]==i)
{ if(j.parent!=null)
succ[(i,j)]=(j,j.parent);
else{
succ[(i,j)]=(j,j);
postnode[j]=0;//j是根结点
}//else
}//if
else if(parent[j]==i)
{ if(lchild[j]!=null)
succ[(i,j)]=(j,j.lchild);
else if(rchild[j]!=null)
succ[(i,j)]=(j,j.rchild);
else succ[(i,j)]=(j,i);
}//if
//给单链表中的每个元素赋权值
if(parent[i]==j)
position[(i,j)]=1;
else
position[(i,j)]=0;
//计算单链表中元素的位序
where 0≤k<log(n-1)+1 do
{ position[(i,j)]=position[(i,j)]+position[succ[(i,j)]];
succ[(i,j)]=succ[succ[(i,j)]];
}//for
if(parent[i]==j) //求结点的后序遍历顺序号
postnode[i]=postion[(i,j)];
}//forall
}
3 结束语
以图1所示的二叉树为例,按照上述算法构造的单链表(带权值)如图5所示。表2为二叉树单链表的位序。

从表2中选出权值为1的边(D,B)、(B,A)、(E,C)、(G,F)、(F,C)、(C,A),所以结点D、B、E、G、F、C、A的位序就是6、5、4、3、2、1、0。即后序遍历顺序号是:1、2、3、4、5、6、7,可得出后序遍历的顺序是D、B、E、G、F、C、A。

一棵有N个结点的二叉树具有(N-1)条无向边。由于要将每条无向边转换成一条向上边和一条向下边,所以它共有2(N-1)条有向边。因此,该算法需要2(N-1)个网格处理单元(处理器),而网格计算技术的发展为并行算法的实现提供了环境的支持。在本算法中求单链表中元素的位序的计算时间复杂度为O(logN),而算法的其余部分的计算时间是常数,所以算法的复杂度为O(logN)。
参考文献
1 严蔚敏,吴伟民.数据结构(C语言版).北京:清华大学出版社,1997
2 Tarjan R E,Vishkin U.An efficient parallel biconnectivity algorithm.SIAM Journal of Computer,1985;1(14)
3 Foster I.The Grid:A New Infrastructure for 21st Century Science.Physics Today,2002;55(2)
4 熊家军,岳大为,李肯立.基于SIMD-SM模型的树的后根遍历并行算法.计算机工程与应用,2002;38(06)
5 Wilkinson B,Allen M.Parallel programming: techniques and applications using networked workstation and parallel computers.Prentice Hall Inc,1999
6 Karp R M,Ramachandran V.Parallel Algorithms for Shared-Memory Machines.Handbook of Theoretical Computer Science,vol A,MIT Press,1990

