摘   要： Petri网是离散事件系统建模的重要工具，本文使用硬件描述语言VHDL实现了基于Petri网的并行控制器。文中通过一个液位控制系统实例具体介绍了这一方法，并通过仿真波形证明了该方法的正确性。这对于离散事件系统并行控制器的设计具有十分重要的意义。
关键词： Petri网  并行控制器  VHDL  可编程逻辑器件

　　Petri网是异步并发系统建模与分析的一种重要工具，1962年由德国科学家C.A.Petri博士创立。40多年来，Petri网理论得到了很大的丰富和发展，其应用领域也在不断扩大，越来越受到国际同行的重视，已成为计算机、自动化和通信领域的热门研究课题。Petri网既有直观的图形表示，又有深厚的数学基础；既是层次化的结构模型，又能反映系统的动态性能[1][2]。用硬件描述语言进行电路和系统设计是当前EDA技术的重要特征，它使得设计者能在较抽象的层次上进行系统结构和内部特征的设计。VHDL作为一种高速的硬件描述语言适于描述设计异步并发的系统，因而可与Petri网模型建立联系。用VHDL对模型进行程序设计，为模型的硬件实现奠定了基础。随着大规模、高密度的可编程逻辑器件FPGA和CPLD的问世与应用方面的迅速推广，并且有各种EDA软件工具的支持，使得人们可以根据Petri网的拓扑结构用硬件加以实现，以使Petri网的硬件实现成为可能。因此，基于Petri网的智能化的并行控制器的设计与硬件实现的课题引起了人们的强烈兴趣。利用Petri网技术，不仅可以用来进行设计、分析和验证，还能够进行优化控制。
　　微电子技术发展到今天，已提供了几千至几千万个标准门的芯片。特别是在系统可编程技术，可有条件地在一个芯片上设计制作一个数字系统，即系统芯片(System on Chip，SoC）。国内市场上常见的Altera公司、Xilinx公司、Lattice公司的FPGA和CPLD芯片，一般都能满足设计SoC的需要，并且都提供了EDA软件开发工具。而且在现有的软件开发工具中，有电路图、状态图、真值表和硬件描述语言等输入方式。但设计片上并行控制器，难以用电路图或逻辑方程输入方式实现；如果用状态图或真值表输入方式，随着问题复杂程度的增加，系统的状态将发生组合爆炸，这是十分棘手的问题。而且有限状态机（FSM）虽已被广泛运用到数字逻辑控制系统，也只是因为它给出了系统化的硬件实现方法和具体的实现模型（如Moore自动机和Mealy自动机），用FSM实现并行控制器也十分困难。因为FSM必须于设计前划分控制器，所以常常会导致非最优的门级实现，且使设计中并发的数量受到使用FSM数量的限制，同时FSM间相互依赖，使得设计难于验证且易产生并行同步错误（如死锁、丢失数据的完整性）。上述这些缺点只有设计遍历整个状态空间时才能验证，因而可能被漏检[3]。若用硬件描述语言输入，遇到的困难是模型和验证。
　　针对传统的设计方法不太适合并行控制器设计的问题，本文介绍一种使用硬件描述语言VHDL来实现基于Petri网的并行控制器的方法。首先使用Petri网对问题进行建模，并对模型进行分析和控制，获得控制器的Petri网模型；然后用VHDL对Petri网控制模型加以描述，得到源文件；最后通过EDA软件开发工具Max+PlusⅡ进行编译、模拟、适配，并下载到可编程逻辑器件中。
1  Petri网简介[2]

2  实现的基本方法
　　Petri网本身就是一种硬件描述语言，是一种高度抽象的、结构化的并发语言。Petri网非常适合于复杂离散系统的建模和形式化分析，而VHDL则是一种标准的硬件描述语言，可以解决数字系统描述中并发性问题，允许其仿真和综合。Petri网和VHDL可以相互补充，并且也可以提供一个验证子系统接收所有设计任务相同的用户接口描述[4]。并行控制器的VHDL文本Petri网描述在一个实际设计中可获得50%的面积减少及40%的速度改善(相对于最好的FSM综合)[4]。
　　用大规模可编程逻辑器件来实现由Petri网描述的并行控制器，其实现的基本步骤如下：
　　(1)对实际系统建立Petri网系统模型。
　　(2)采用Petri网软件工具对所建立的Petri网系统模型进行分析并加以控制，建立监控器的Petri网系统模型。
　　(3)确定输入输出变量并选择相应的FPGA或CPLD器件。
　　(4)根据网的拓扑结构确定条件与事件间的逻辑关系，用硬件描述语言如VHDL对Petri网模型进行描述。
　　(5)以VHDL描述作为设计输入，通过EDA软件开发工具，如ispDesign EXPERT或Max＋PlusⅡ等，进行编译、模拟、适配，然后下载到器件中。
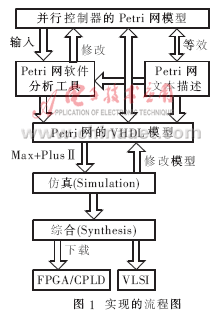
　　整个硬件实现的流程图如图1所示。

3  基于Petri网的并行控制器设计举例
3.1 系统描述
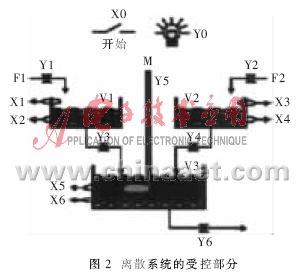
　　从文献[5]中选择了一个如图2所示的并行控制器设计例子，这是一个用于说明离散事件系统控制器设计的典型示例。它有3个盛放液体的罐子：V1、V2、V3，其中V1、V2是用来盛放不同种液体F1、F2的，M是搅拌系统的驱动电机。系统停止时，指示灯Y0亮。当起动按钮按下时（X0=1），阀Y1、Y2打开，2种不同的液体F1、F2分别注入V1、V2。当V1中的液体到达X1位置时，Y1关闭；当V2中液体到达X3时，阀Y2关闭。当V1、V2中的液体分别都到达X1、X3时，Y3、Y4同时打开；当V1、V2中液体分别都低于X2、X4时，Y3、Y4关闭，同时Y6打开。当V3中液体高于X5时，Y5闭合，电动机M开始搅拌；当V3中液体流出低于X6时，Y6关闭，指示灯亮，重新回到原来状态。

3.2 系统控制部分的控制解释Petri网模型
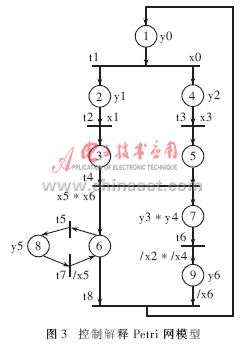
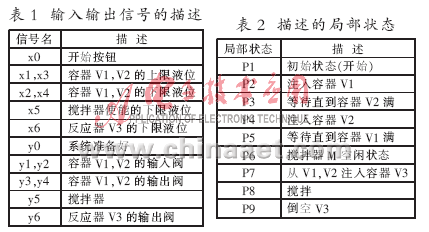
　　用Petri网对系统控制部分进行描述，得到的控制解释Petri网模型如图3所示。模型中输入输出信号的描述如表1所示，描述的局部状态如表2所示。

3.3 模型的VHDL实现
　　用VHDL实现的部分源代码如下：
　　t1<=not p2 and not p4 and x0 and p1；
　　t2<=not p3 and x1 and p2；
　　t3<=not p5 and x3 and p4；
　　t4<=not p6 and not p7 and p3 and p5；
　　t5<=not p8 and x5 and x6 and p6；
　　t6<=not p9 and not x2 and not x4 and p7；
　　t7<=not p6 and not x5 and p8；
　　t8<=not p1 and not x6 and p6 and p9；
　　np1<=t8 or (p1 and not t1)；
　　np2<=t1 or (p2 and not t2)；
　　np3<=t2 or (p3 and not t4)；
　　np4<=t1 or (p4 and not t3)；
　　np5<=t3 or (p5 and not t4)；
　　np6<=t4 or t7 or(p6 and not t5 and not t8)；
　　np7<=t4 or (p7 and not t6)；
　　np8<=t5 or (p8 and not t7)；
　　np9<=t6 or (p9 and not t8)；
3.4 基于Max+PlusⅡ的并行控制器仿真
　　在MAX+PlusⅡ中经编译后进行功能仿真，仿真波形如图4所示。波形表明结果是正确的。

4  结  论
　　Petri网是并发系统强有力的建模工具，通过对Petri网模型的分析，可以获得系统的许多结构和动态性能，根据控制策略，还可以建立系统的控制模型并获得系统在控制作用下的性能。以上讨论证明，基于Petri网的并行控制器可以用VHDL实现，从而开辟了并行控制器设计与实现的新途径。
参考文献
1   David R，Alla H著，黄建文，赵不贿译.佩特利网和逻辑控制器图形表示工具(GRAFCET).北京：机械工业出版社， 1996
2   袁崇义．Petri网原理.北京：电子工业出版社，1998
3   Pardey J，Amroun A，Bolton M et al.Parallel Cotroller Synthesis for Programmable Logic Devices.Microprocessors  and Microsystems，1994；18（8）
4   Fernandes J M，Adamski M，Proenca A J.VHDL Generation  from Hierarchical Petri Net Specifications of Parallel Controllers.IEEE ProcComput Tech，1997；144(2)
5   Adamski M.A Rigorous Design Methodology for Reprogrammable Logic Controllers. Proceedings of the International Workshop on Discrete-Event System Design DESDes′01.Przytok：Technical University of Zielona Góra，2001