CDMA移动通信系统具有抗干扰能力强,保密性好,容量大等优点,受到广泛的关注。CDMA是利用码序列的正交性和准正交性区分不同用户,它是在同频、同时的条件下,各个接收机根据信号码型之间的差异分离出需要的信号。由于CDMA系统中同一频率在所有的小区重复使用,CDMA中的干扰特别严重,若没有先进的功率控制技术,尽可能减小用户的背景干扰,就会产生严重的误码现象。随着用户数的增加,信号的信噪比急剧下降。当低于一定门限时,就可能发生通信中断。由于CDMA系统存在传输衰减、多址干扰、远近效应等问题,系统容量受限于用户间的相互干扰,因此,必须对功率进行控制。本文主要针对CDMA系统中的功率控制算法进行研究。
1功率与容量的关系
在CDMA系统中,由于发射功率的制约或系统自身的干扰,CDMA系统的容量受到限制。在反向链路上,当一个移动台的功率不足以克服其他移动台的干扰时,系统达到容量极限。在前向链路上,当基站的总功率没有多余的部分分配给一个新的用户时,系统达到昂大容量。即当一个基站为使其全部用户正常的运行而发射的总功率超过基站的额定功率时,前向链路就达到受功率限制的容量。
为了接入一个呼叫,CDMA移动台的功率必须大到足以克服带宽内其他CDMA移动台产生的干扰,即必须达到一定的信号干扰比。在任意给定时刻,移动台所需要的发射功率取决于从移动台到基站的路径损耗和所有反向链路总的干扰电平。后者取决于其他CDMA移动台的数量和位置。
所有的移动台每建立一个新呼叫就提高了干扰电平,每一移动台也就必须相应地增加发射功率以保持呼叫的完整性。这个过程随着移动台的增加而反复进行,直到达到一个极限值。达到这个极限时,任何一个新的移动台,无论其位置在哪,都无法以足够的功率来克服,而现有的移动台也没有足够的功率来克服新呼叫产生的附加干扰。小区内所有呼叫都要具有相同的Eb/I0要求,这个限制表现为要求小区基站接收到的信号强度都等于一个相同的值。对于任何一个移动台,小区内的干扰即为(N-1)S,N为小区内的移动台的数目。来自小区外移动台的共道干扰是一个次级的干扰源,它的大小可以取为小区内干扰的部分值(β倍)。由于周围移动台的发送强度相对较低,且路径损耗距离更远,由此产生的干扰电平通常可以由β<1来表征,这个值小于小区基站的噪声电平。与小区干扰不同,小区外的移动台的干扰不是通过本小区基站的接收机进行功率控制,所以干扰大小更难确定,然而仅需要知道外部移动台的总体影响即可。
由于共道干扰电平相对较小,对于周围满负载的小区也可采用相同的β值,对于大的N值,所有的干扰可以由话音激活因子来减小。
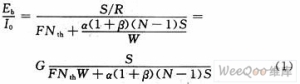
式中:Eb为比特能量;I0为热噪声加干扰的功率谱密度;F为基站噪声指数;Nth为热噪声的功率谱密度;S为接收信号强度;R为比特速率;α为话音激活因子;β为干扰因子;N为小区内移动台的数目;W为系统带宽;G=W/R为处理增益。热噪声密度Nth,CDMA带宽W和基站噪声指数F之积称为基站噪声。
小区基站接收机所要求的Eb/I0取值的范围是关于移动台速度和多径条件的慢衰落,不同的类型的用户为保持一定的FER就有不同的Eb/I0要求。高速移动用户与低速和静止情况相比EB/I0也不相同。
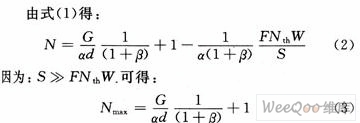
式中:d为所需的Eb/Ib。当使用13 Kb/s声码器时,对于一个扇区大约为24。重写表达式(1)得每个用户平均需要的信号功率为:

从图1可知,每个用户所需的小区基站的信噪比随小区负载的加重而非线性增加,负载越大,斜率越陡,小区付出的平均功率代价要大的多。因此,每增加一个移动用户,一个高负载的小区比一个低负载的小区付出的代价大,另外,负载过重的小区将不能响应其用户话音激活的统计波动。进一步调整式(1)以反映总的接受干扰Prec=α(1+β)NS。Prec与基站噪声之比可以由小区负载u=N/Nmax完全表示出来,从图2可看出干扰是随小区负载非线性增加的。

功率和负载之间的关系可以表示为总功率(接收信号加基站噪声)与基站噪声之比为:
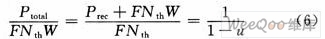
从图3上可看出每次增加容量的一半时,总功率与基站噪音之比就增加一倍,例如当负载从0 dB增加到0.5 dB时,总功率与基站噪音之比从0 dB增加到3 dB;当负载从0.5 dB增加到0.75 dB时,这个比值就从3 dB增加到6 dB。
2功率控制信道仿真模型
为了实现功率的实时控制,在信道中不仅考虑由阴影和路径损失所引起的慢衰落,而且要考虑由多径传播引起的快衰落。
其中:r是基站与移动台的距离;α是路径损耗指数;ξ是均值为0,标准方差为σ的高斯随机变量。σ和α的典型值为8 dB和4 dB,如图4所示。
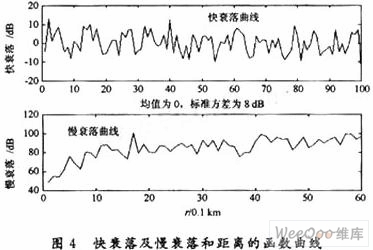
如图4所示,慢衰落是基于距离的函数,在很短的时间内(如几个ms),用户与基站间的距离没怎么大的变化,因此为了方便系统仿真,暂且可以看作是不变的。对于快衰落,本次仿真采用Jakes提出的一种模拟移动通信衰落技术的Jakes模型。移动台与基站的相对运动引起的接收电平的频率变化,称为多普勒频移,最大频移fm=υm/λ其中υm是最高车速,λ是载波波长,ωm=2πfm。瑞利衰落过程可以通过叠加N个复正弦曲线来近似,这组正弦曲线的频率和相位由特定的公式给出。定义N0=(1/2)(N/2-1),则衰落信道的信道函数T(t)可以表示为:
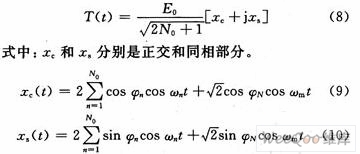
式中:ωn=ωmcos(2πn/N),n=1,2,…,N0;φN是最大多普勒频率正弦曲线的初始相位,φn=第n个多普勒频移正弦曲线的初始相位。移动台的速率为50
km/h(13.9 m/s),多普勒频移fm=41.6 Hz。N0=8,φN=0。采用Matlab进行仿真,如图5所示。
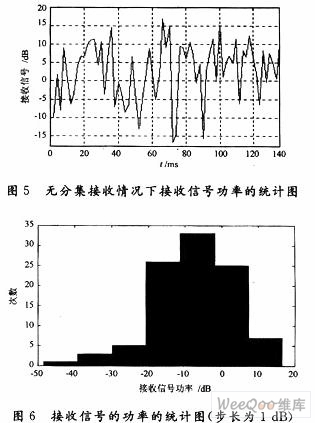
从图5可看出,固定步长功率控制算法在无分集接收情况下,接收信号有很强的“过冲”现象,这是由于系统根据上一时刻的接收信号的功率的强度来决定下一时刻的功率调整方向,而且每次的功率控制在系统出现深度衰落的时刻,就会无法即时补偿,而在控制误差很小时,将引起很大的波动。接收信号的功率的统计图如图6所示。
从图6可以看出,实际接收的信号在期望值的附近波动,而且分布的两边是非对称。比较步长为1 dB的图6和步长为0.5 dB的图7,可发现在相同的衰落情况下,步长为1 dB的算法比较适合。从这里也可看出步长的取定与具体环境(如衰落程度和背景干扰)有关,这也是固定步长功率控制的弊端所在。

3结语
这种功率控制算法,允许基站发送功率控制命令,用户通过控制命令,以固定的步长调整发射功率,功率改变的过程就像一个“乒乓”控制,这种控制方法的系统稳定性差,且有很大的过调量和稳定时间。单纯从功率控制的角度,提高控制精度的方法有两种。一是提高功率测量速度,相应地提高功率控制的频度,从而增大相邻的两个样点的相关程度以达到提高控制精度的目的;另一种方法是提高控制量的精调程度,每次控制命令用多个比特来表示,从而提高控制精度。

