摘 要: 针对非降采样轮廓波变换(NSCT)具有多尺度、方向性和平移不变性等特点,为改善融合后图像模糊现象,提出了一种基于区域特性的非降采样轮廓波变换的多聚焦图像融合算法。该算法结合NSCT的特点,将图像进行NSCT,变换为不同方向的各子带信息;然后基于局部均值和局部方差选择低频子带系数,并在带通方向子带中引用局部方向对比度作为测量算子来选择带通方向子带系数;最后,通过反变换得到融合图像。实验结果表明,本算法融合效果优于传统的加权平均、小波变换及NSCT算法。
关键词: 多聚焦图像融合;非降采样轮廓波变换;区域特性
图像融合是指将两幅或多幅包含不同信息的图像融合成一幅信息量最大化的图像,以获得更多信息。传统的图像融合算法大体可以分成两类[1-2]:一类在空间域上,对匹配后的源图像直接进行加权平均处理,从而得到一幅新的融合图像。这种方法简单易行,但容易使得到的融合图像产生明显的人工拼接痕迹。另一类是基于变换的方法,该方法将多尺度变换作为抽取图像显著特征的工具,包括图像金字塔分解的算法[3-4]、基于小波的方法[5-6]和基于非降采样轮廓波变换NSCT(Nonsubsampled Contourlet Transform)[7]。随着小波理论的发展,小波分析逐渐成为图像融合领域的研究热点。但由于小波融合算法具有有限个方向,在水平、垂直、对角方向的缺乏使得小波变换不能充分利用图像本身的几何正则性,容易丢失图像中的细节信息。
NSCT具有多尺度、方向性和平移不变性等特点,可以有效提取待融合图像中的方向信息,使得融合后的图像更好地满足人眼的视觉要求。
本文主要研究多聚焦图像的融合,将具有平移不变性的NSCT引入图像融合,根据NSCT分解方向子带特点[7],提出一种新的基于局部区域特性的NSCT自适应多聚焦图像融合算法。该算法基于局部均值和局部方差选择低频子带系数,并在带通方向子带信息中引用局部方向对比度作为测量算子来选择带通方向子带系数,改善融合后图像模糊现象。实验结果也验证了该算法的有效性。
1 非降采样轮廓波变换基本理论
4小波变换因其良好的时域和频域局域性, 被广泛用作图像多尺度几何分析工具。但是小波变换难以表达二维图像中边缘的奇异性。针对小波变换在图像处理中的缺陷,DO M N和VETTERLI M于2002年提出了一种新的图像多尺度几何分析工具——Contourlet变换[8]。Contourlet变换是在离散域中直接给出图像的Contourlet变换定义,采用滤波器组实现图像的多尺度、多方向分解。Contourlet变换将多尺度分析和多方向分析分开进行,首先使用拉普拉斯金字塔LP(Laplacian Pyramid)变换对图像进行多方向分解,以捕获图像中的奇异点,然后对每一级LP分解所获得的高频分量采用方向滤波器组DFB(Directional Filer Bank)进行多方向分解,将同方向上的奇异点连接成轮廓段,从而实现对图像的多尺度、多方向分解。但是,采用Contourlet变换对图像进行分解和重构的过程中需要对图像进行降采样和上采样操作,使得Contourlet变换缺少平移不变性。为此,CUNHA A L等人提出了一种具有平移不变特性的Contourlet变换——NSCT变换。
NSCT采用非降采样塔式滤波器组NSPB(Nonsubsampled Pyramid FilterBank)和非降采样方向滤波器组NSFB(Nonsubsampled Directional FilterBank)对图像进行迭代分解。其结构如图1所示,其理想频域划分示意图如图2所示。与Contourlet变换不同,NSCT去掉了LP分解和DFB分解中信号经分析滤波后的下采样抽取和综合滤波前的上采样插值,而是对对应的滤波器进行上采样,再对信号进行分析滤波和综合滤波。因此,所有的分解后的低频和高频子带与输入图像大小相同,NSCT的完全平移不变性、多尺度和多方向扩展的特性应用到图像融合中恰到好处,能够更加有效地提取源图像的轮廓特征,使融合过程中特征提取和处理更加方便,并可以在融合图像中保留更多有效的原始特征,从而得到更优的融合效果。

2 融合方法
多聚焦图像的特点是每幅图像的某一部分清晰,一部分模糊。本文针对这个特点,提出了一种基于NSCT的区域自适应多聚焦图像融合算法,根据离焦光学系统成像原理以及人眼视觉特性,给出了各子带图像的融合规则。
2.1 融合步骤
(1)对配准好的图像A、B分别进行NSCT分解,得到尺度系数和一系列带通方向子带系数;
(2)对A、B的低频子带系数和各带通方向子带系数应用不同的融合规则进行融合,得到融合后的系数;
(3)进行NSCT反变换,得到融合图像F。


3 实验结果及性能分析
为了验证算法的性能,在NSCT TOOLBOX上进行了有效验证,并与加权平均方法、小波融合方法和NSCT的融合算法进行了对比。
为了对实验结果进行客观的评价,实验选取了一些结合标准图像的评价方法对实验结果进行评价。选取的客观评价标准有信息熵(H)、均方根误差(RMSE)、相似性度量(S)和峰值信噪比(PSNR)。
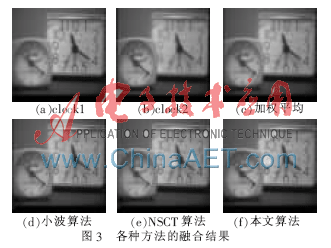
将多种不同的融合方法进行了对比,如图3所示。从人眼视觉来看,加权平均算法损失了图像的清晰度,比较模糊;小波算法和NSCT算法的细节虽然保留地比较完整,但是清晰度也有一定的损失,本文算法的结果的清晰度比其他算法的结果稍好。各项性能参数比较如表1所示。
从表1可以看出,本算法获得了更小的均方根误差、更高的相似度和峰值信噪比,都优于其他算法。从实验结果可以看出,本算法有效保证了图像的清晰程度(熵值较高),并有效地减少了图像的失真。实验结果表明,本算法是一种有效可行的融合方法。
本文在NSCT的基础上,提出了一种基于区域特性的自适应多聚焦图像融合算法,讨论了各子带系数的融合规则。从表1中可以看出,本算法能够从源图像中提取更多的有用信息。实验结果从主观和客观方面与其他图像融合方法进行了比较,证明了该方法的有效性。
参考文献
[1] 常霞,焦李成.基于非降采样Contourlet的多传感器图像自适应融合[J].计算机学报,2009,32(11):1-15.
[2] Yang Xiaohui, Jiao Licheng. Fusion algorithm for remote sensing images based on nonsubsampled contourlet transform[J].Acta Automatica Sinica, 2008,34(3):274-281.
[3] BURT P, ADELSON E H. The Laplacian pyramid as a compace image code[J]. IEEE Transaction on communication,1983,31:532-540.
[4] TOET A, VAN RUYVEN L J, VELATON M. Merging thermal and visual image by a constrast pyramid[J]. Optional Engineering, 1989, 28:789-792.
[5] 王丽,卢迪,吕剑飞.一种基于小波方向对比度的多聚焦图像融合方法[J].中国图像图形学报,2008,13(1): 145-150.
[6] 孙巍,王柯,袁国良,等.基于复数小波域的多聚焦图像融合[J].中国图像图形学报,2008,13(5):951-957.
[7] CUNHA A L, ZHOU J P, DOM N. The nonsubsampled contourlet transform: theory, design, and applications[J].IEEE Transactions on Image Processing,2006,15(10):3089-3101.
[8] DO M N, VETTERLI M. The contourlet transform: an efficient directional multiresolution image representation[J].IEEE Trans Image Proc, 2005, 14(12):2091-2106.
[9] Zhang Qiang, Guo Baolong. Fusion of multifocus images based on the nonsubsampled contourlet transform[J]. Acta Photonica Sinica,2008, 37(4):838-843.
[10] 刘涛,张登福,何宜宝.基于区域分割和非降采样轮廓波变换的多聚焦图像融合算法[J].计算机应用,2010,30(10):2805-2807.
[11] 刘晓红,姜吉涛,周雪芹.基于局部方差的安全玻璃碎片自动检测算法[J].测绘科学技术学报,2007,24(5):374-376.

