摘  要： 针对基于小波变换的阈值去噪方法仅适用于去除高斯白噪声，对于脉冲噪声得不到好的降噪效果的问题，提出了将基于高斯模型的小波变换算法与改进的中值滤波相结合的去噪方法。该方法能够有效去除高斯白噪声和脉冲噪声的混合噪声。仿真实验结果表明，结合算法去噪后图像的峰值信噪比和均方误差都比单一算法得到了改善，从而证明了该方法的有效性。
关键词： 中值滤波；改进的中值滤波；小波变换

    图像信号在其形成、传输、变换以及终端处理中，经常会受到各种噪声的干扰而降质。噪声的来源取决于实际的应用环境，由于环境复杂，噪声特性也非常复杂。例如，图像传输过程中受到强干扰时会产生脉冲噪声，在激光和超声波图像中常存在乘性椒盐噪声，而照明的不稳定、镜头灰尘以及非线性信道传输引起的图像退化等都将产生不同种类的噪声。仅去除某一种噪声无法达到最佳的图像去噪效果。目前,针对图像去噪的研究热点[1]是利用小波变换去除图像中的高斯白噪声,然而这种方法无法很好地去除图像中的脉冲噪声,如何在充分利用小波理论[2]的前提下,去除图像中的混合噪声成为图像去噪领域中亟待解决的重要课题。
    传统的图像去噪方法基于噪声和信号的统计特性不同，采用空间域低通滤波的方法来进行去噪。其中，中值滤波法(Median Filter)[3]是广泛应用于去除脉冲噪声的一种非线性滤波去噪方法，它对脉冲噪声有很好的抑制能力，但当滤波窗内的干扰样本数(像素数)大于窗长一半时，中值滤波没有滤波效果。此时，依靠增加滤波窗尺寸，固然可以提高噪声滤除能力，但是损失了图像细节。此外，中值滤波法对高斯分布和均匀分布噪声的抑制能力显著下降。近年来，许多国内外的学者研究发现基于小波变换的阈值去噪法对于高斯分布和均匀分布的噪声有很好的抑制能力。如果图像信号中既有脉冲噪声又有高斯噪声或白噪声，那么单独用这些方法都是行不通的。因此，本文提出一种基于高斯模型（GMM）的小波变换算法与改进的中值滤波相结合的方法,能较好地解决滤除混合噪声的问题。
1 中值滤波法
    中值滤波是基于排序统计理论的一种能有效抑制噪声的非线性信号处理技术，广泛用于去除脉冲噪声。基本原理是把数字图像或数字序列中一点的值用该点的一个邻域中各点值的中值代替。该滤波器的本质是一种滑动窗口滤波器,滤波操作是使滑动窗口中心位置的信号抽样值取代当前窗口内的所有抽样的中位值。中值滤波算法严格的数学定义如下：

 

4 实验结果与分析
    在仿真实验中，加入不同强度的高斯白噪声和不同密度的脉冲噪声，然后用不同的方法来去除混合噪声，将本文提出的结合算法与单一的改进中值滤波算法、单一的基于高斯混合模型的小波去噪算法(GMM)作比较。从图1的比较中可以看出，采用结合算法的去噪效果明显地比单一改进的中值滤波算法和GMM算法的效果要好，它的去噪效果更彻底，对高斯噪声和脉冲噪声都能进行有效的滤除，并且具有更好的保留图像细节和边缘信息的能力。

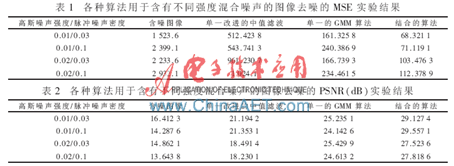
    表1和表2分别列出了含有混合噪声图像用各种算法去噪后的均方误差(MSE)和峰值信噪比(PSNR)。从表1和表2中也可以看出，结合方法去混合噪声的效果是最好的，去噪后均方误差最小、峰值信噪比最高。

参考文献
[1] 谢杰成，张大力，许文立.小波图像去噪综述[J].中国图象图形学报，2002，3(7)：209-217.
[2] 陈武凡.小波分析及其在图像处理中的应用(第1版)[M].北京：科学出版社.2002.
[3] KASPARIS T，TZANNES N S，CHEN Q.Detail-preservingadaptive conditional median filters[J].Electic.Image，1992，14(1)：356-364.
[4] CHANG G，YU B，VETTERLI M.Spatially adaptive wavelet thresholding with context modeling for image de-noising[J]. IEEE Trans on Image Processing，2000，9(9)：1522-1531.
[5] 侯建华，田金文.基于贝叶斯最大后验估计的局部自适应小波去噪[J].计算机工程，2006，32(11)：13-15.