摘  要： 提出了一个销售量问题：不同的厂家有不同的商品，他们想知道相同商品在市场上的销售总量，但各自都不透露自己的私有数据。同时提出了一个解决销售量问题的协议，并且在半诚实模型下对协议的安全性和计算复杂度及通信复杂度进行了分析。
关键词： 多精度；安全多方求和；保密性；公平性

    目前，关于安全多方计算问题的研究主要包括保护私有信息科学计算问题、保护私有信息计算几何问题、保护数据挖掘问题和安全多方统计分析问题等。前人在安全多方计算问题的实际具体研究上已经有了很大的研究成果。本文提出了安全多方计算在统计中的一个新的应用。
    例如，有n个经营同一品牌不同产品的厂家，如生产手机、MP3和电视机等，他们想知道在市场上同一产品的销售总量。在这种情况下，各个公司同一产品的销售量应该是保密的，最后要计算出同一产品在市场上的销售总量。
    本文利用安全多方求和提出了一个解决上述问题的协议，并在半诚实下对该协议的正确性和安全性给出了证明，也计算出了计算复杂度和通信复杂度。本文假设参与各方都是“半诚实的”，即参与各方都能严格执行协议的规定和流程，不会中途强行退出或恶意掺入虚假数据。但在协议执行过程中他们可能会保留所有能搜集到的关于其他参与方的信息，以期望在协议结束后推断出其他参与方的输入信息。人们对安全多方协议的研究有很多是基于半诚实的，因此对基于半诚实模型下安全协议的研究是非常有意义的。
1 基本概念
1.1 多精度运算
    机器直接处理的整数有一定的限制，当算法中出现的整数超过了这个限度，就需要多精度算法[1]。多精度运算就是用多个字节来存储这个整数，将整数之间的运算转换成字节间的运算。
1.2 安全多方计算[2]
    安全多方计算是指拥有秘密输入的互不信任的n方，希望用各自的秘密输入共同去计算一个约定的函数。在计算结束之后，每一方都能接收到正确的输出，并且每一方只能了解自己的输入和输出，而不知道其他方的输入和输出。它能够使参与者在不泄露各自输入秘密的前提下完成协作计算的任务。
1.3 安全多方求和
    安全多方求和是指参与计算的多方成员，在保护各自输入数据隐私的情况下，共同计算一个函数之和。假设有n个用户(C1，C2，…，Cn)参与计算，每个用户Ci有自己的私有数据xi，他们共同计算，但任何一方都不愿意向其他方泄露自己的私有数据[3]。
 

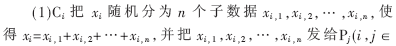
    以上通过安全多方求和方法进行计算的方案协议，除了最终的计算结果外，不泄露公司的任何数据秘密，实现了保密计算的功能。
3 实例说明
    现有6个公司对同一品牌的3个不同产品(手机、MP3和电视机)进行销售量的计算。M值为10万。销售情况如表1所示。

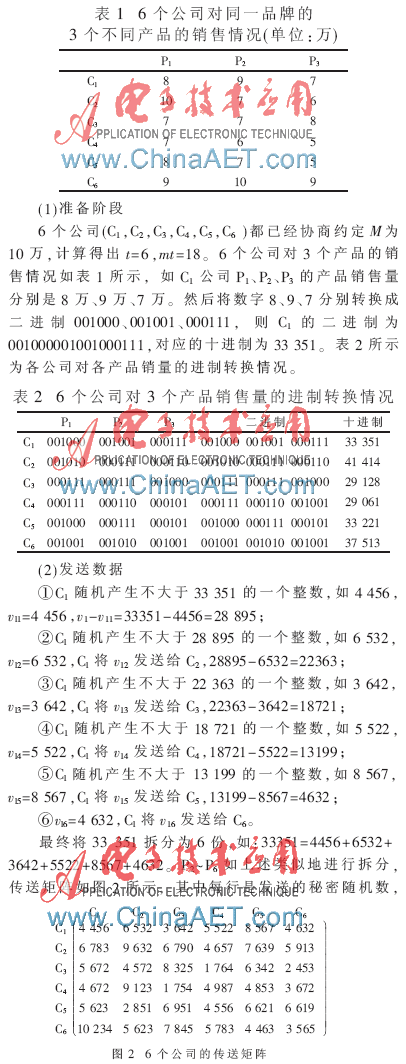
 每列是接收的秘密随机数。

  (3)计算结果
    C1从传送矩阵中得到第一列随机数{4 456，6 783，
5 672，4 672，5 623，10 234}，求出它们之和是37 440。C1公开把37 440发送给所有其他的Cj(j∈[1，n],j≠i)，类似地，C2～C6分别都公开发送自己得到的随机数之和。那么，每个Ci(i∈[1，n])得到的随机数之和为{37 440，38 333，35 307，27 269，38 485，26 854}，得到它们之和是203 688，即是所有产品的销售总量，其对应的二进制序列为{110001101110101000}，则P1、P2、P3对应的二进制分别为{110001}、{101110}和{101000}。因此可知产品P1、P2、P3的销售总量分别为49万、46万、40万。
4 性能分析
    性能分析主要从安全性和计算复杂度及通信复杂度来进行。
4.1 安全性分析
    定理1 如果参与评审的成员是半诚实的，则上述协议是安全的。
    (1)公平性：n方可以独立同时完成计算并知道结果。单个成员不与其他成员合作，无法提前计算，因此协议具有公平性。
    (2)保密性：由于n方对数据先随机拆分，再利用安全多方求和方法计算。每方只能接收到数据拆分后的一小部分，无法得到整个数据，因此数据具有完全保密性。
4.2 复杂度分析
    （1）计算复杂度
    由于上述协议的计算复杂度是多精度运算的，每方在准备阶段对数据随机划分进行了n-1次，所以多精度减法就执行了n-1次，在计算结果阶段计算接收到的所有数据之和，多精度加法执行了n-1次，此方案中多精度整数的比特位数为mt(t=[log2(n×M)]+1)，则每一方的计算位复杂度为O(nmlog2(n×M))，总的计算位复杂度为O(n2mlog2(n×M))。
    （2）通信复杂度
    上述方案在发送数据和计算结果阶段各进行了n(n-1)次通信，则通信复杂度为 O(n2)，而每个数据的长度不超过m([log2(n×M)]+1)，所以通信的位复杂度为 O(n2log2(n×M))。
    本协议是一个新的安全多方计算协议的实际应用，可以用于电子评审系统、统计学中的数据求和问题，此外还可以用于计算学生的总（平均）成绩却不泄露自己的任何消息给其他学生。在本协议中，若参与方的成员增多或数据值增大，计算复杂度和通信复杂度也会增大，但数据的保密性却更好。因此如何降低计算复杂度和通信复杂度还需进一步研究[5]。
参考文献
[1] ROSEN K H.Elementary number theory and its applications[M].New York：Addition Wesley，1984.
[2] 冯登国.安全协议——理论与实践[M].北京：清华大学出版社，2011.
[3] 曹天杰，张永平，汪楚娇.安全协议[M].北京：北京邮电大学出版社，2009.
[4] 仲红，黄刘生，罗永龙.基于安全多方求和的多候选人电子选举方案[J].计算机研究与发展，2006，43(8)：1405-1410.
[5] 仲红，黄刘生，罗永龙.一个实用的电子评审方案[J].小型微型计算机系统，2007，28(1)：178-181.