在自适应阵列处理中，由于多径效应或智能干扰的存在而使期望信号与干扰相干，直接应用常规波束形成器会引起期望信号相消，使波束形成性能急剧下降[1]。因此存在相干干扰时的自适应波束形成技术已引起人们广泛的关注。在相干信号环境下，根据不同的应用情况，阵列信号的处理准则[2]有三种，第一种准则是把期望信号和与之相干的干扰信号有效组合起来，使阵列输出信干噪比达到最大；第二种是约束期望信号方向增益恒定，而使得干扰加噪声的输出功率最小；第三种是在约束期望信号增益恒定的基础上，不管干扰是否与期望信号相干，均约束干扰信号增益为零，并使得干扰加噪声的输出功率最小。参考文献[3]利用第一种准则，使方向图在期望信号与相干干扰信号方向均形成峰值，导致期望信号淹没在相干干扰中，不利于接收。参考文献[4]提出自适应加权空间平滑算法（AWSS），通过虚拟波束形成，自适应形成子空间的权值，阵列接收效果较好，但它没有使用对角加载，因而当期望信号方向估计有误差时，性能严重恶化。参考文献[5]的多约束方法（MCMV）利用第三种准则，对相干干扰施以强制零陷约束。该方法因信号方向角估计误差敏感，稍有偏差，性能便急剧下降。参考文献[6]提出的辅助变换方法（CTMV），利用第二种准则，通过非强约束的方式，用一个转换矩阵来预处理接收数据，去除期望信号，保留相干干扰不变，阵列接收效果较好。由于其对非相干干扰未进行任何处理，所以性能改善有限。最近提出的一种基于不确定集约束的稳健波束形成方法[7]，通过对一定范围内的期望信号及相干干扰加以约束，稳健性，但是不确定集即角度范围不容易确定。本文提出一种辅助变换类算法(ICTMV)，利用第二种准则，设计的变换矩阵对期望信号、相干干扰和非相干干扰信号三者都进行处理。仿真结果表明，该算法提高了干扰抑制、输出信干噪比等性能。

 
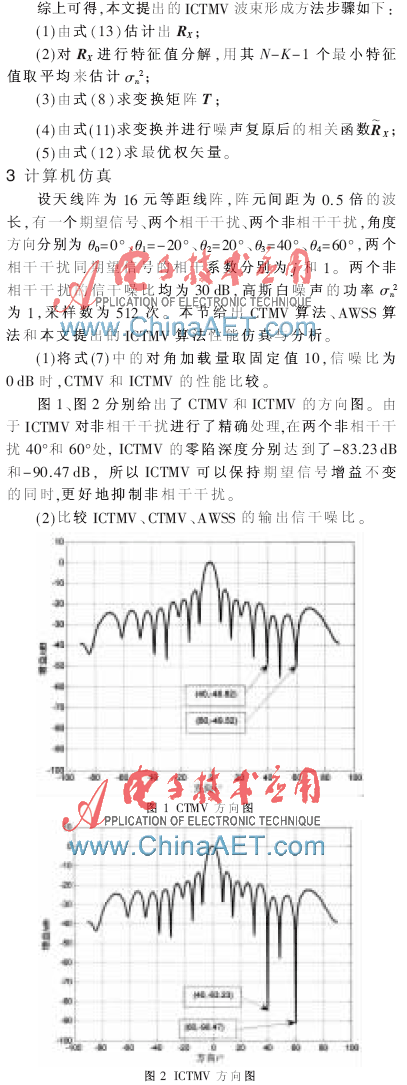
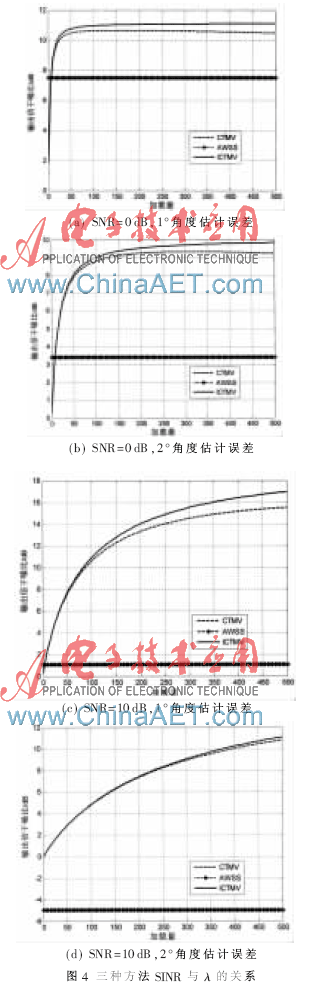
    图3所示λ取10，三种方法的输出信干噪比与输入信干噪比的关系曲线图。由于ICTMV的变换矩阵T对非相干干扰也进行了等式变换，所以随着信噪比的增加，它的输出信干噪比几乎线性增加，而另两种方法的输出信干噪比则间断式增加，因此ICTMV大大改善了输出信干噪比。

    (3)对角加载量由0~500逐渐变化时，输出信干噪比的变化。
    信噪比为0 dB，期望信号、相干干扰信号角度估计存在1°、2°误差时，图4(a)、图4(b)分别给出了输出信干噪比随对角加载量的变化；信噪比为10 dB,期望信号、相干干扰信号角度估计存在1°、2°误差时,  图4(c)、图4(d)分别给出了输出信干噪比随对角加载量的变化。AWSS的输出信干噪比不受加载量变化的影响，这是由于AWSS未采用对角加载。对角加载量取得越大，则ICTMV的输出信干噪比将比CTMV的大得越多。

　　(4)信号角估计误差从-2°到+2°变化时，输出信干噪比的变化。
      信噪比为0 dB，期望信号、相干干扰信号角估计都存在估计误差时，对角加载量取10和100时，ICTMV、CTMV和AWSS法的输出信干噪比随角估计误差的变化如图5所示。由图可见，本文所提出的ICTMV算法在整个角度估计误差范围内，比CTMV和AWSS有更高的输出信干噪比，因而稳健性更强。

    当存在相干干扰时，本文提出一种改进的辅助变换ICTMV波束形成方法。设计了一种变换矩阵对期望、相干干扰、非相干干扰信号三者都能进行精确处理；使用对角加载，对干扰尤其是非相干干扰抑制更深。该方法具有更高的输出信干噪比和更强的稳健性。
参考文献
[1] WIDROW B, DUVALL K M, GOOCH R P, et al. Signal cancellation phenomena in adaptive antennas:Causes and cures[J]. IEEE Transactions on Antennas and Propagation, 1982,30(5):469-478.
[2] BRESLER Y, REDDY V U, KAILATH T. Optimum beamforming for coherent signal and interferences[J]. IEEE Transactions on Acoustics, Speech, Signal Processing, 1988, 36(6): 833-843.
[3] 赵永波，张守宏. 存在相干干扰时的最优波束形成[J].通信学报，2002，23(2)：113-121.
[4] 丁前军，王永良，张永顺，等.一种虚拟波束形成自适应加权空间平滑算法[J]. 电子与信息学报，2006，28(12):2263-2268.
[5] YEH C C, WANG W D. Coherent interference suppression by an antenna array of arbitrary geometry[J]. IEEE Transactions on Antennas and Propagation, 1989,37(10):1317-1322.
[6] SUNG L T, TSAI L T. Coherent interference suppression with complementally transformed adaptive beamformer[J]. IEEE Transactions on Antennas and Propagation,1998,46(5):609-617.
[7] YU L, LIU W, LANGLEY R J. Novel robust beamformers for coherent interference suppression with direction-of-arrival estimation errors[J]. IET Microwaves Antennas and Propagation,2010,4(9):1310-1319.
[8] 张贤达. 矩阵分析与应用[M]. 北京：清华大学出版社，2004:255-305.