摘 要: 设计了一种基于LabVIEW软件平台及BP神经网络算法、支持向量机(SVR)、偏最小二乘(PLS)等分析算法的化学分析系统。系统以LabVIEW软件为基础,以调用MATLAB作为数据分析核心,以达到自动快速的分析目的。该系统还可将各种回归分析后的数据进行对比,并做出拟合曲线,效果直观、清晰。此系统作为虚拟仪器测量系统的数据分析模块,具有一定应用价值。
关键词: LabVIEW;BP神经网络算法;支持向量机算法;偏最小二乘算法;液体推进剂
自20世纪许多新型仪器及技术被引入分析化学以来,分析测试已逐步实现自动化和计算机化,使其在分析测试过程中,可以非常方便地得到大量可靠的测量数据。这些数据都以二维或多维的形式存在,如何将复杂数据降维,挖掘数据中包含的信息,是分析工作者面临的重要问题[1]。化学计量学作为一门建立在多学科基础上的横向学科,主要就是针对化学测量数据信息的分析处理和提取,这一学科在数据分析、化学模式识别、谱图解析、构效关系等方面,发挥着举足轻重的作用[2]。
本文提出的基于LabVIEW及化学计量学的化学分析系统,结合虚拟仪器技术和BP神经网络、支持向量机、偏最小二乘三种分析算法,对前端虚拟仪器测试系统的多维数据进行回归分析,并比较三种方法的效果优劣,保存最佳回归模型,建立数据库。系统总体框架如图1所示。

1 系统设计原理
本系统基于LabVIEW软件开发平台,利用 MatlabScript节点实现在LabVIEW中调用MATLAB脚本的功能,从而充分利用LabVIEW图形化设计语言的优点和MATLAB强大的数据处理能力,使得开发的化学虚拟仪器系统具有功能更强的数据处理能力[3]。该系统程序设计主要包括数据分析和数据库管理两大模块,系统主页前面板如图2所示。其中,数据分析模块包括数据读取、模型建立、回归分析、预测;数据库管理查询主要包括数据存储、查询、修改、提取分析等功能。

系统主要应用嵌入式子面板和弹出式子面板两种技术。数据分析模块采用的是嵌入式子面板技术,即利用函数选板中的子面板控件,将子VI嵌入主VI中,从而使分析方法的选择与分析执行过程变得直观且清晰;数据库访问模块应用的是弹出式子面板技术,即利用应用程序控制选板中的打开VI引用控件,进行子VI的静态调用。
1.1 数据分析模块
1.1.1 BP神经网络分析模块
BP神经网络算法流程可以分为BP神经网络构建、BP神经网络训练和BP神经网络预测[4]。当参数适当时,BP神经网络算法能够收敛到较小的均方差,是目前应用最广的神经网络算法之一。本文BP神经网络分析模块,主要是利用LabVIEW调用MATLAB神经网络工具箱中关于BP神经网络的newff、sim和train 3个函数[5],进行BP网络建模和数据分析预测,其面板如图3所示,包括输入向量路径选择、向量数组显示、回归拟合结果图和输出向量数组显示等功能。

1.1.2 支持向量机分析模块
支持向量回归SVR(Support Vector Regression)算法的基础主要是ε不敏感函数(ε-insensitive function)和核函数算法。SVR采用核函数解决这一矛盾,用核函数代替线性方程中的线性项可以使原来的线性算法“非线性化”,即能作非线性回归。与此同时,引进核函数达到了“升维”的目的,而增加的可调参数却很少,这样即便是过拟合也仍能控制[6]。
本系统支持向量机分析模块,主要利用LabVIEW调用基于MATLAB平台的LIBSVM工具箱中的SVMcgForRegress、svmtrain和svmpredict 3个函数[7],依据支持向量回归方法建立非线性模型。由于LIBSVM工具箱单维输出的特点,对样本的多种组分应分别建立3个回归模型,进行数据集的非线性回归。支持向量机算法子VI前面板及程序框图分别如图4、图5所示。


1.1.3 偏最小二乘分析模块
偏最小二乘方法(PLS)作为一种常用的分析算法被广泛地应用于分析化学研究中。这种方法不仅吸收了经典最小二乘法的优点,同时是主成分回归(PCR)方法的进一步发展。
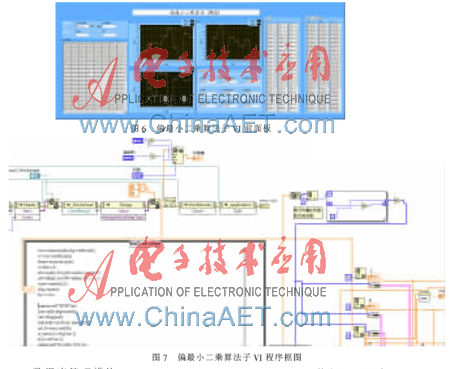
偏最小二乘回归的基本原理是[8]:考虑p个变量y1,y2,…,yp与m个自变量x1,x2,…,xm的建模问题,首先在自变量集中提出第一成分t1(t1是x1,x2,…,xm的线性组合,且尽可能多地提取原自变量集中的变异信息);同时在因变量集中也提取第一成分u1,并要求t1与u1相关程度达到最大;然后建立因变量y1,y2,…,yp与t1的回归。如果回归方程已达到满意的精度,则算法中止;否则继续第二对成分的提取,直到能达到满意的精度为止。若最终对自变量集提取r个成分t1,t2,…,tr,则偏最小二乘回归将通过建立y1,y2,…,yp与t1,t2,…,tr的回归式,然后再表示为y1,y2,…,yp与原自变量的回归方程式,即偏最小二乘回归方程式。图6所示为偏最小二乘算法分析模块前面板,图7所示为偏最小二乘算法子VI程序框图。该程序主要应用了LabVIEW中的report generation工具箱对Excel表格中的训练数据进行读取,并转化成二维数组形式;再将训练集数据输入MATLAB脚本中,进行偏最小二乘算法分析;最后利用report generation将训练结果和预测结果生成Excel表格,存储至数据库。
1.2 数据库管理模块
由三种算法分析预测的数据和建立的模型都被存储在数据库中,随时可以进行调用。由虚拟仪器的测试测量系统得到的数据将存储于数据库中,以构建数据训练集。用户可随时调用历史数据进行模型训练和模型训练效果的比较。图8为数据库管理模块前面板。

LabVIEW可以通过基于ADO技术的LabSQL数据访问包,以调用子VI的方式进行数据库访问。ADO通过与开放数据互连ODBC(Open Database Connectivity)连接可以访问任何支持ODBC的数据库,本系统采用Microsoft Access数据库来进行数据管理、存储和查询。
(1)数据存储模块。首先是建立Access数据源,在Access中建立一个名为MyDB.mdb的数据库,同时在配置DSN时将数据源命名为DSN_Wastewater monitoring,之后就可以在LabVIEW中进行调用LabSQL的函数功能。
(2)历史数据查询模块。同样利用LabSQL的ADO Connection Create.vi和ADO Connection Open.vi创建数据库连接,通过SQL Execute.vi执行SQL语句“SELECT*FROM 数据库名 WHERE 选择条件”将所需数据抽取出来,在前面板的表格控件中显示数据,并且进行格式转换及输出数据趋势的曲线图标。
2 结论及展望
利用此系统的三种算法对某液体推进剂(3个组分的混合物)滴定数据进行回归分析,得到如表1所示的分析结果。
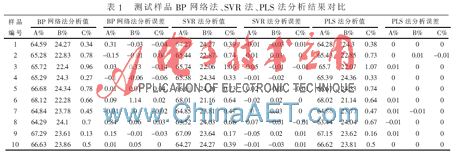
(1)三种模型的分析结果都在可接受误差范围之内,可作为此液体推进剂的滴定分析结果。
(2)三种分析模型中,偏最小二乘模型的结果较佳。三种组分的标准误差:BP法分别为9.62×10-2、1.58×10-1、3.40×10-3;SVR法分别为2.87×10-2、1.01×10-3、6.67×10-5;PLS法分别为5.56×10-5、2.22×10-5、1.11×10-5。
(3)基于LabVIEW及化学计量学的化学分析系统,操作简便,人机界面友好,实现了测试数据自动分析处理,并实时获得结果,避免了繁琐的文本程序编译计算过程,提高了测试结果的精度,大大缩短了分析时间。
(4)利用LabVIEW的共享变量或Web Server网络编程方式,可以为用户提供一个集算法计算、模型共享、数据共享为一体的化学分析网络平台。
(5)通过对某种液体推进剂分析数据的验证,该系统运行良好,结果准确,可作为虚拟仪器测试系统的数据处理模块,具有一定应用价值。
(6)本系统将引入更多多元回归算法[9],如主成分分析、多元线性回归、多元非线性回归算法。随着本系统引入算法种类的不断增加,效果的不断优化,系统功能将逐渐完善,可以进行如一元回归、多元线性、多元非线性及多维的回归分析预测。
(7)随着网络的普及,随着算法可靠性的增加以及算法使用方便性的增加,会吸引大量的科学研究工作者在该系统平台上进行计算和程序开发,其各方面价值会逐步体现。
参考文献
[1] 许禄.化学计量学方法[M].北京:科学出版社,2004.
[2] 倪永年.化学计量学在分析化学中的应用[M].北京:科学出版社,2005.
[3] 曲丽蓉,胡容,范寿康.LabVIEW、MATLAB及其混合编程技术[M].北京:机械工业出版社,2011.
[4] 周开利,康耀红.神经网络模型及其MATLAB仿真程序设计[M].北京:清华大学出版社,2005.
[5] MATLAB中文论坛.MATLAB神经网络30个案例分析[M].北京:航空航天大学出版社,2010.
[6] 邓乃样,田英杰.数据挖掘中的新方法—支持向量机[M].北京:科学出版社,2005.
[7] 丁世飞,齐丙娟.支持向量机与算法研究综述[J].电子科技大学学报,2011,40(1).
[8] 王惠文.偏最小二乘回归方法及其应用[M].北京:国防工业出版社,2000.
[9] MILLER J N, MILLER J C. Statistics and chemometrics for analytical chemistry, fouth edition[M]. England: Pearson Education,2000.

