摘 要: 针对Mean Shift算法跟踪效果不佳以及粒子滤波算法计算量大且实时性不强等问题,提出了一种结合Mean Shift和粒子滤波的运动目标跟踪融合算法。首先用Mean Shift算法进行跟踪,在跟踪结果不佳的情况下用粒子滤波算法进行修正。实验结果表明,融合算法很好地结合了两种算法的优点,既保留了Mean Shift算法的实时性,又很好地体现了粒子滤波算法的鲁棒性,实用性很强。
关键词: 算法融合;均值漂移;粒子滤波;运动目标跟踪
运动目标跟踪广泛地应用在生活中的各个领域,比如在交通监控中,目标跟踪对有效地预防交通事故起到至关重要的作用[1-2]。为了提高跟踪效果,目标跟踪领域产生了大量的新方法。由于单一算法所具有的局限性,近年来,人们尝试使用算法融合来提高目标跟踪的性能。多数情况下,算法融合提高了目标跟踪性能。
Mean Shift(均值漂移)是一种有效的跟踪算法,具有很高的精度和速度[3]。但是,当光照强度不佳或者运动目标速度很快的时候,Mean Shift算法的跟踪效果就会变得很差。而Particle Filter算法处理这种情况的效果要好于Mean Shift算法,但是运算速度远低于Mean Shift算法。本文融合两种算法的优点来提高跟踪效果。首先建立一个反馈系统,先用Mean Shift算法对目标跟踪,当跟踪效果不理想时,再用Particle Filter算法进行跟踪。仿真结果表明,在绝大多数情况下该方法比用单一算法的跟踪效果好。
1 Mean Shift算法
Mean Shift算法最早由Fukunaga等人于1975年在一篇关于概率密度梯度函数的文章中提出来的,其最初含义恰如其名,就是指偏移的均值向量,在这里,Mean Shift是一个名词,指代一个向量。1995年,Cheng Yizong等发表了一篇关于Mean Shift的重要文献[5],在这篇文献中,Cheng Yizong对基本的Mean Shift做出改进,首先定义了一族核函数,然后设定了一个权重系数。这两方面的改进大大拓展了Mean Shift的应用范围。
本文所用的Mean Shift算法步骤如下[4]:首先使用一种非参数概率密度来建立一个色彩分布模型描述跟踪目标,用Bhattacharyya系数(巴氏系数)确定目标物体与背景的相似点,然后取概率平均值来确定运动目标最有可能移动的区域。算法过程如下:
假设目标物体中心位于x0,设{xi}i=1…n为目标物体的标准像素点,b(xi)表示xi点的RGB值,则目标物体的特征值u=1...m的概率定义如下:

2 Particle Filter算法
粒子滤波PF(Particle Filter)的思想基于蒙特卡洛方法(Monte Carlo Methods),它是利用粒子集来表示概率,可以用在任何形式的状态空间模型上[6]。其核心思想是通过从后验概率中抽取的随机状态粒子来表达其分布,是一种顺序重要性采样法(Sequential Importance Sampling)。简单来说,粒子滤波法是指通过寻找一组在状态空间传播的随机样本对概率密度函数进行近似,以样本均值代替积分运算,从而获得状态最小方差分布的过程。这里的样本即指粒子,当样本数量n→∞时,可以逼近任何形式的概率密度分布[7]。
在大多数情况下,粒子滤波可以得到比Mean Shift更好地跟踪效果,但是,粒子滤波算法需要大量的运算,这将大大降低跟踪速度。
粒子滤波算法的跟踪过程大致如下[8]:
(1)初始化:在运动目标可能出现的区域随机生成n个粒子,每个粒子的概率相同;
(2)观测更新:计算n个粒子的置信度,归一化权值,确保所有粒子的权值和为1;
(3)估计目标状态:根据粒子的权值和所对应的位置,计算出目标最有可能移动的位置;
(4)重采样:去掉置信度低的粒子,加入新的置信度高的粒子,确保粒子总数为n,这些粒子即为下一时刻的初始化样本粒子;
(5)如需继续跟踪,则返回步骤(2),否则退出。
3 Mean Shift和Particle Filter的融合算法
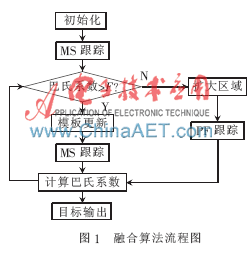
Mean Shift算法可以快速有效地跟踪到运动目标,但在非线性、运动目标部分遮挡的情况下,跟踪效果会变得很差,而Particle Filter算法在这种情况下的跟踪效果依然令人满意[9-10]。但是,Particle Filter存在粒子选取的问题。针对这两种算法的优缺点,本文将这两种算法进行了有效地融合,很好地弥补了单一算法存在的不足。算法的主要步骤如下:
(1)初始化目标模型A;
(2)从视频中读取一帧图像,用Mean Shift算法进行跟踪;
(3)计算出跟踪结果,把这个结果标记为候选区域B;
(4)计算巴氏系数Ba(A,B);
(5)当巴氏系数大于阈值F,表明跟踪效果良好,则更新模型,继续用Mean Shift算法跟踪;
(6)如跟踪效果不好,则扩大候选区域B的范围,使用粒子滤波算法进行跟踪,直到跟踪效果令人满意;
(7)更新模型,继续从第(2)步开始进行跟踪;
(8)如停止跟踪,则算法终止。
融合算法流程如图1所示:
4 实验结果分析
分别采用Mean Shift算法和本文所提出的融合算法对同一目标进行跟踪,以验证算法的有效性,用Particle Filter算法进行跟踪误差分析。开发环境为MATLAB R2008b,首先以人为目标观察光照条件不佳的情况下的跟踪效果,然后以高速运动的物体为目标观察高速运动情况下的跟踪效果,目标的初始状态均用鼠标手动标定。实验结果如图2~图5所示。

从4组实验结果来看,与Mean Shift算法相比,在光照条件不佳或运动目标速度很快的情况下,融合算法在保证跟踪实时性的同时,还能够保持足够的准确性。同时,本文算法的一个关键是阈值F的选取。由第三部分介绍可知,选取一个合适的阈值,可以提高跟踪的性能,由于缺少测试视频,所以只能采用排除法来选取阈值F,经过多次试验所得到的结果,阈值F大概在Ba×0.85~Ba×0.9之间最适合进行跟踪实验。
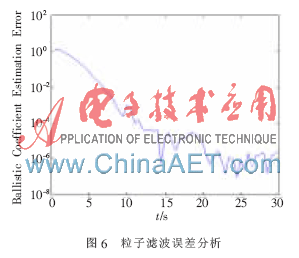
而对于粒子滤波,虽然随着跟踪时间的增加跟踪误差变小(如图6所示),但是算法运行时间过长,跟踪的实时性得不到保证。本文提出的融合算法则在保证准确性的同时,兼顾了实时性。
本文根据Mean Shift算法和粒子滤波算法的优缺点,提出了一种融合两种算法的方法。该算法保留了Mean Shift算法跟踪快速的优点,同时又兼具了粒子滤波鲁棒性强的特点。最后,对本文提出的算法进行了具体的实现,实验结果令人满意。
由于本文是对手工标定的区域进行跟踪,因此,实现跟踪窗口的自动跟踪和自适应窗口将是下一步的研究工作。
参考文献
[1] COMANICIU D, RAMESH V, MEER P. Kernel-based object tracking[J]. IEEE Transactions Pattern Analysis and Machine Intelligence, 2003,25(5):550-585.
[2] YILMAZ A, JAVED O, SHAH M. Object tracking: a survey[J]. ACM Computer Surveys, 2006,38(4):23-67.
[3] COMANICIU D, RAMESH V, MEER P, Real-time tracking of non-rigid objects using Mean Shift[C]. Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition,2000,2: 140-149.
[4] 孙剑,周凤岐,周军.基于mean-shift的快速跟踪算法设计与实现[J].计算机工程,2006(8):24-43.
[5] Cheng Yizong. Mean-shift, mode seeking and clustering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1995, 17(8): 780-799.
[6] 姚剑敏.粒子滤波跟踪方法研究[D].长春:长春光学精密机械与物理研究所,2004:50-81.
[7] NUMMIARO K, KOLLER M E, VAN G L. A color-based particle filter. Proceedings of the 1st Workshop on Generative- Model-Based Vision, 2002:43-65.
[8] ARULAMPALAM M S, MASKELL S, GORDON N, et al. A tutorial on particle filters for online nonlinear/non-gaussian bayesian tracking[J]. IEEE Transactions on Signal Processing,2002,50(2):154-188.
[9] COMANICIU D, MEER P. Mean shift: a robust approach toward feature space analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002(24):603-619.
[10] 马丽,常发亮,乔谊正.基于均值漂移算法和粒子滤波算法的目标跟踪[J].模式识别与人工智能,2006,19(6):767-793.

