摘  要： 从串扰的原理及串扰和差分阻抗之间的内在联系出发，通过模型变换和公式推导，给出了近端串扰系数和差分阻抗之间的关系式。再以平衡结构的带状线为例，得到了平衡结构带状线的近端串扰的估算公式。在相同条件下与Hyper Lynx仿真软件结果进行比较，验证发现估算结果与仿真结果基本符合。
关键词： 近端串扰；差分阻抗；带状差分线；前仿真

    随着半导体工业的飞速发展，具有高集成度、高速接口的器件在电子产品中的应用越来越广泛，由此产生的信号完整性问题也越来越复杂。串扰是信号完整性问题中的一类关键问题。串扰是指一个网络通过耦合在另外一个网络产生了有害的噪声。通常把噪声源所在的网络称为攻击网络或攻击线，而把有噪声产生的网络称为受害网络或受难线。在物理空间中任何两个网络之间都会存在串扰，而且串扰不仅会发生在网络的信号路径上，还会产生在信号的返回路径上。串扰产生的根本原因是由于存在边缘场，根据麦克斯韦定律，只要有电流存在，就会有磁场存在。当两个磁场相距很远时，磁场干扰很微弱，基本可以忽略；但是当两个网络相距很近时，其中一个网络的磁场就会在另一个网络的信号路径或信号返回路径上产生磁场干扰，这个干扰就是串扰的来源。
    通常用n节集总电路模型来描述串扰(如图1所示)[1]。在这个模型中存在两条传输线，传输线１用单位长度电容CL1和单位长度电感LL1表示，传输线２用单位长度电容CL2和单位长度电感LL2来表示。它们之间的容性耦合用单位长度互容CmL表示，感性耦合用单位长度互感LmL表示。

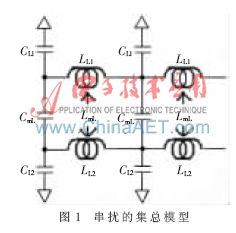
    根据测量端的不同，串扰又可以分为近端串扰和远端串扰。近端指受害网络上靠近攻击网络驱动器的一端，远端指远离攻击网络驱动器的一端。近端串扰和远端串扰出现的噪声形式不同。近端噪声的特性是迅速上升到一个饱和值，并且保持该值2TD时间，然后再下降。这个恒定的近端噪声饱和量就称为近端串扰系数。通常计算和仿真的就是近端串扰系数[2]。
    另外，当两根导线靠近时，差分阻抗会变小；当两根导线远离时，差分阻抗就会变大。这种变化的背后就是差分线间的互容互感，而串扰的来源就是互容互感。因此可以通过对差分线模型的研究来寻找一种可靠、快速的近端串扰算法。本文从常见的差分阻抗公式入手，通过建模和算法变换得到CmL/CL和LmL/LL的取值范围，然后再估算出近端串扰系数的取值范围。
1 近端串扰算法
    常用的近端串扰系数计算公式[3]：
    
    从上式可以发现，近端串扰系数是一个百分比，由比值CmL/CL和LmL/LL组成。如果能够得到CmL/CL和LmL/LL的值，或者知道它们的取值范围，就可以知道近端串扰系数的值或者取值范围。一般情况下可以通过仿真软件提取到相关的参量值。但是使用仿真软件来做串扰仿真需要建立专门的仿真工程，会比较麻烦，而且有时还会碰到软件许可等问题。
    在了解差分阻抗之前，首先了解一下传输线阻抗的定义。通常阻抗定义为电压与电流之比。在传输线中，这个定义仍然有效，传输线上任何一处的瞬时电压与瞬时电流成正比，流过传输线的瞬时电压和瞬时电流的比值就称为瞬态阻抗。传输线的瞬态阻抗仅由传输线的横截面和材料特性共同决定，瞬态阻抗等于施加的电压与流过器件的电流的比值。特性阻抗是传输线的固有属性，仅与材料特性、介电常数、频率有关，而与传输线的长度无关。只要这两个参数不变，瞬态阻抗就是一个常数。对于一个均匀的传输线，任何一处的瞬态阻抗都是相同的，这样一个恒定的瞬态阻抗就称为传输线的特性阻抗[4]。
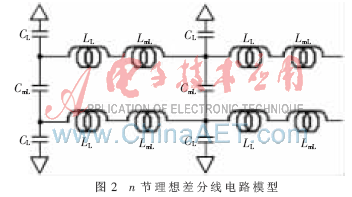
    差分阻抗就是差分信号的特性阻抗，它等于差分信号电压与电流的比值。如果差分线之间相距很远，它们之间的耦合会小到可以忽略不计，差分阻抗就可以近似等于两个单根信号阻抗之和。当差分信号线逐步靠近时，它们之间的边缘场就会互相覆盖，相互的耦合程度就会越来越强。假设图1中传输线１和传输线２相同，即CL1=CL2，LL1=LL2，同时传输线上传送的是差分信号，那么串扰的n节集总电路模型就与差分线的n节集总电路模型相同。可以把图1的模型转换成图2的n节理想差分线电路模型[5]。
    将图2的模型简化，就可以得到图3所示的理想的差分线集总电路模型。

2 验证
    为了验证估算式(11)的准确性，选用Mentor的Hyper Lynx来做对比试验。验证对象选择常见的带状差分线（如图4所示），其由两根相互平行的导线和两个包裹它们的参考平面组成。带状差分线设置：线宽w=4 mil，参考平面之间的距离b=12 mil，铜厚t=0.5 oz。带状线长度分别取为1 in、2 in、4 in、8 in。
    实验激励信号源设置：Vo=3 V，r/f=1 ns。

    验证的结果如表1所示。从表1可以看到，当耦合长度小于饱和长度时，近端串扰系数与耦合长度正相关；当耦合长度大于饱和长度后，近端串扰系数不再增加，保持一个常量。这个结果和近端串扰的特性相吻合。

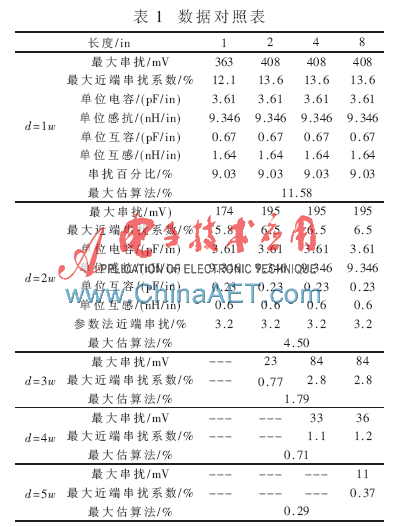
    将估算结果与仿真结果进行比对。从仿真结果中提取两组参数，其中一组是最大串扰，另一组是提取了单位长度的LmL、LL、CmL和CL的参数。从这两组数据分别得到最大近端串扰系数结果和参数法近端串扰系数结果。将估算法的结果和上述两组结果比较后发现，估算值介于最大近端串扰系数和参数法近端串扰系数之间。这个结果与预期的结果相吻合。最大近端串扰系数由于考虑了最恶劣的环境，会在真实的结果上放大，保证有足够的裕量，因此会比估算值大。估算值本身考虑了取值的区间，它在两头的取值都以极限的形式存在，因此它的最大值会比参数法计算的结果大。
    经过验证，估算法确实达到了预期的效果，它可以提供相对准确的估算结果，而且使用简便快速，是仿真方法无法比拟的。当然估算法也有一些缺陷，它与实际结果之间还是有一些误差，而且公式也有一定的适用范围，不适用于耦合过程中电场变化和磁场变化比较大的情况，除非加矫正系数。在今后的研究中，需要不断地对其进行补充和完善，使其保持速度优势的情况下进一步提高结果的精确性。
参考文献
[1] BOGATIN E.信号完整性分析[M].李玉山，李丽平，译.北京：电子工业出版社，2005.
[2] JOHNSON H，GRAHAM M.High-speed digital design[M]. New Jersey：Prentice Hall PTR，1993.
[3] JOHNSON H.High speed signal propagation[M].New Jersey：Prentice Hall PTR，2003.
[4] 陈伟，黄秋元，周鹏.高速电路信号完整性分析与设计[M]. 北京：电子工业出版社，2009.
[5] 梁昌红，王新稳，李延平，等.微波技术与天线[M].北京：电子工业出版社，2011.
[6] 郑君里，应启衍，杨为理.信号与系统(第3版)[M].北京：电子工业出版社，2011.