摘   要： 提出了新的基于特征点的高速图像匹配算法。该算法把角点特征和灰度值特征结合起来，定义了一种基于Harris角点的灰度值特征，并充分利用角点灰度值以及角点周边灰度值和位置信息，然后依据这些信息进行匹配。实验结果表明，该算法不仅速度快，而且对灰度值分布不均图像和含噪图像的匹配同样适用。
关键词： 图像匹配；特征点；灰度值；Harris角点；噪声

    图像配准[1](Image Registration)是指同一个目标的两幅或两幅以上的图像在空间位置的对准。图像配准的过程称为图像匹配(Image Match)。图像配准应用十分广泛，例如航空航天技术、图像镶嵌与融合、地理信息系统、医学图像分析、虚拟现实和机器人视觉等领域。国内外很多学者在图像匹配方面做过很多研究，但是尚未有一种普遍适用的方法可以解决各类图像匹配问题，大多数方法都是针对实际应用中遇到的问题而提出的。常见的图像匹配方法依据其匹配方法的不同[2-4]可以分为基于灰度[5]、基于特征[6]和基于理解[7]3种。基于灰度的图像匹配方法具有精度高的优点，但是也存在如下缺点：对图像的灰度变化较敏感，尤其是非线性变化的光照变化，将大大降低算法的性能；计算的复杂度高；对目标的旋转、形变以及遮挡比较敏感。基于特征的图像匹配方法可以克服基于灰度的图像配准方法的缺点，图像的特征点要比图像的像素点少得多，因此可以大大减少匹配过程中的计算量；特征点的提取过程可以减少噪声的影响，对灰度变化、图像形变以及遮挡等都有较好的适应能力。基于理解的图像匹配技术尚在起步阶段，还没有显著进步。本文算法结合了基于灰度的图像匹配方法和基于特征的图像匹配方法，首先利用Harris角点检测算法找到角点，然后在已找到的角点基础上定义新的特征点，并以此特征点作为匹配依据进行匹配。实验表明，该算法不仅速度快，而且对灰度值分布不均图像和含噪图像的匹配同样适用。
1 传统模板图像匹配算法
    传统的基于灰度的模板图像匹配技术[8]是将模板T在搜索图像S上移动，在模板覆盖下的那块搜索图称为子图Si,j，i,j为这块子图的左上角像素点在S图像中的坐标，称为参考点，其中1<i<L-N+1，1<j<K-M+1。比较T和Si,j，若两者相同，则参考点坐标（i,j）所在的位置就是模板图像在搜索图像S中的位置。模板匹配算法示意图如图1所示。

2 基于Harris角点的快速匹配算法
2.1 Harris角点检测
    Harris角点检测算法由HARRIS C和STEPHENS M于1988年在参考文献[9]中提出,是对参考文献[10]中Moravec角点检测算子的扩展。Moravec角点检测算法的主要缺点是不能准确找出全部角点，没有对图像进行降噪处理，因此其响应对噪声敏感，尤其是对边缘响应很敏感。Harris算法受信号处理中自相关函数的启发，给出了与自相关函数联系的矩阵M。M阵的特征值是自相关函数的一阶曲率，如果在图像中某点的行列曲率值都高，则认为该点是特征点。Harris算法的表达式为：

2.2 基于Harris角点的图像特征点
     为实现快速和精确的图像匹配，本文在图像Harris角点的基础上定义了新的特征点，并以此特征点作为匹配依据。
     在说明算法之前，先给出如下定义。
    定义1  一阶特征点：在所有检测到的Harris角点中，角点的灰度值在与其八邻域的灰度值的和中所占的比例最大的点。
    当检测到相同的一阶特征点，即两个像素点都是一阶特征点，但是在图像中所处的位置不同，那么类似可以定义二阶特征点，即考虑一阶特征点领域内24个点，然后再以二阶特征点作为匹配依据，其他各阶特征点可类似定义。
　　以基于Harris角点为基础的灰度值特征点作为匹配依据，减少了计算量的同时利用了灰度值的精确性。特征点的选取方式决定了其对噪声不敏感，对灰度分布不均匀的匹配问题同样适用。
    算法的步骤如下：
    (1)用Harris角点检测算法对模板图像T进行检测，找到角点；
    (2)在检测到的Harris角点中找到一阶特征点，若存在多个一阶特征点,则寻找更高阶的特征点。不对参考图像S做角点检测是因为参考图像通常较大，消耗较多时间；
    (3)在参考图像S中找到所有灰度值与一阶特征点灰度值相同的点，并且计算其灰度值与八邻域灰度值和的比例与一阶特征点是否相同，若相同,则该点所在的位置即为模板图像上的特征点在参考图像上的位置。
    本文找到的模板图像上的点和参考图像上对应的点并不是传统模板图像左上角的点，但经过简单换算即可知道左上角点的位置以及待配准图像在参考图像中的位置。
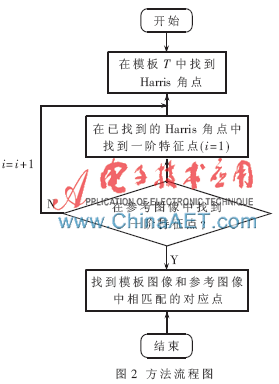
    图2所示为该方法的具体流程。

3 实验结果分析
     为了验证本文匹配算法的有效性，分别使用了一组参考图像和相应模板图像进行了实验。实验环境为:Intel（R）Core(TM) i3 M370 2.40 GHz CPU，2 GB DDR3内存，Windows 7 旗舰版，MATLAB 7.7.0。图3为模板图和参考图匹配结果,其中参考图像是256×256的lena图，模板图像大小为67×67。模板图左上角像素点在参考图中坐标为(60,70),匹配的特征点对坐标分别为(2,36)和(61,105)。

     为了说明本文算法速度上的优越性，将本文算法分别与传统模板匹配算法、序贯相似性检测算法[11](SSDA)进行了比较,共进行了100次匹配，实验结果如表1所示。

     本文在经Harris角点检测处理过的图像的基础上，定义了一种灰度值特征，并以此灰度值特征作为匹配依据。实验证明，与传统模板算法和SSDA算法相比，本文算法在保留精确性的同时具有更快的速度，并且对含有噪声的图像也能很好地找到匹配点。本文算法也有一定的局限性，当模板图像角点特征不明确时,可能由于检测不到角点而导致方法失效。
参考文献
[1] 赵小川. 现代数字图像处理技术提高及应用案例详解(MATLAB版)[M].北京:北京航空航天大学出版社，2012.
[2] RADKE R J，ANDRA S，AL-KOFAHI O，et a1． Image change detection algorithms：a systematic survey[J]． IEEE  Transactions on Image Processing，2005，14(3)：294-307．
[3] 陈景航，杨宜民．一种基于Harr小波的快速模板匹配算法[J]．计算机工程，2005,31（22）:169-171.
[4] ZITOVA B，FLUSSER J．Image registration methods：a survey[J]． Image and Vision Computing，2003，21(11)：977-1000．
[5] THORNTON J，SAVVIDOS M． A bayesian approach to deformed pattern matching of iris image[J]． IEEE Pattern Analysis Machine Intelligence，2007，29(4)：596-606．
[6] JAIN A K，CHEN Yi． Pores and ridges： high-resolution  fingerprint match using level3 features[J]． IEEE Pattern Analysis Machine Intelligence，2007，29(1)：15-27．
[7] KOLMOGOROV V．Graph based algorithms for scene re．construction from two or more views[D]． New York: The Graduate School of Cornell University，2004．
[8] STEFANO L D，MATTOCCIA S．ZNCC-based template matching using bounded partial correlation[J]．Pattern Recognition Letters，2005(26)：2129-2134．
[9] HARRIS C， STEPHENS M． A combined corner and edge detector[C]. Proceedings of the 4th Alvey Vision Conference，1988：147-151．
[10] MORAVER H P． Towards automatic visual obstacle avoidance[C]． Proceedings of International Joint Conference  on Artificial Intelligence，1977：584-590．
[11] BARNEA D I，SILVERMA N H F． A class of algorithms  for digital image registration[J]．IEEE Thansations on Computer， 1972，C-21(2)：179-186.