摘  要： 平坦Rice信道是一种应用范围广泛的移动衰落信道。精度和运行速度间的矛盾是SOS模型难以解决的固有矛盾。基于SOS模型和查表法，设计了一种平坦Rice衰落信道模拟器。理论和仿真分析结果表明，该模拟器同时具备高精度和高速度的良好特性，有较强的实用价值。
关键词： Rice信道；正弦波叠加法；查表法；模拟器

　无线通信技术研究的本质是基于不同的信道特性开发与信道特性相适应的高可靠性、高有效应通信技术。因此，信道模拟器不可避免地成为了无线通信研究领域的一个研究热点。研究表明[1-3]，较之目前多数人采用的Rayleigh衰落，Rice衰落能更好地描述大多数现实中存在的无线信道。在不考虑多径或多径不可分辨时，Rice衰落信道可用平坦Rice信道模拟器来模拟。当Rice因子为零时，Rice信道模拟器退化为Rayleigh信道模拟器；当Rice因子无穷大时，等价于Gaussian信道。因此研究Rice信道模拟器更具实用性。衰落信道建模的主流方法有：正弦波叠加法SOS（Sum-of-Sinusoids）和成型滤波器法[1-2]两种。SOS法建立信道模拟器，简称SOS模型，与成型滤波器法相比，其运算量小、设计灵活简便，是目前被广泛采用的方法。前人[3-4]提出的SOS Rician信道模拟器均假设直射径LOS（Line-of-Sight）时不变或为常数。而实际的Rice信道LOS径通常是时变的，甚至具有随机性。因此，这些模拟器并不能精准地反映LOS径的物理特性，从而使整个模拟器的精度受到影响。Xiao Chengshan[5]提出了一种基于SOS模型的平坦Rice信道模拟器，该模拟器在实现过程中对散射径和直射径均引入随机变量，更切实地模拟还原了实际信道，然而却以牺牲速度为代价。要达到其理论精度，这种模拟器在运行时必须求取多次统计平均。
　用SOS法设计信道模拟器存在一对不可调和的矛盾，即精度与速度之间的矛盾。仿真器的随机性越好，就越逼近理想的信道特性，即精度越高。然而，要得到高随机性的模拟器必须在生成信道时经过多次运算求取统计平均，这势必加大运算量，严重降低了仿真速度。单纯使用SOS法难以解决速度与精度的矛盾。SOS法的运算量主要集中在谐波三角函数运算上，为了提高速度，可将查表法与SOS法相结合，用查表法代替谐波三角函数运算。C S Xiao模拟器是一种精度较高的Rice信道模拟器。本文在该模拟器的基础上融入查表法，设计了一种Rice信道模拟器。理论分析和对比仿真结果表明，该模拟器极大地提高了仿真速度，具有很强的实用性。

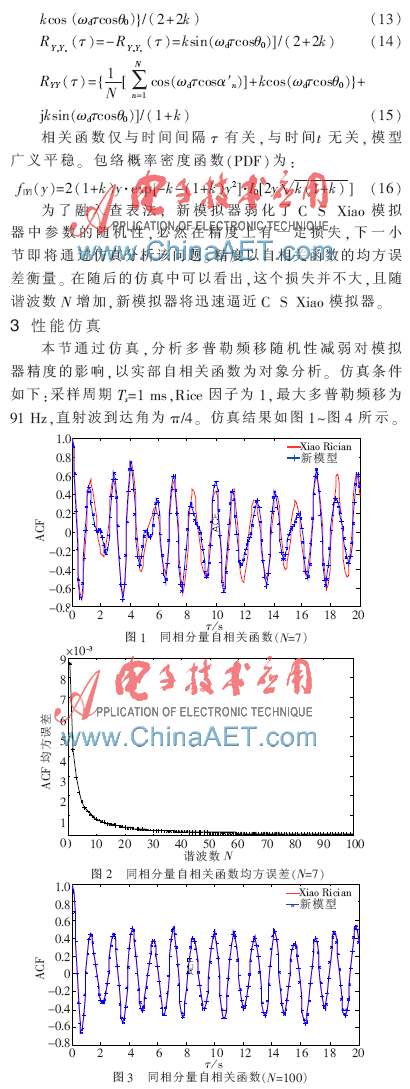
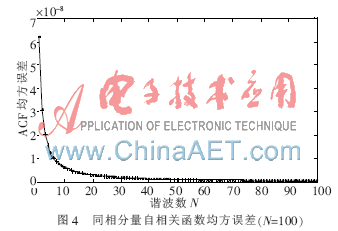
　当取N=7时，新模拟器与C S Xiao模拟器统计特性曲线单从自相关函数曲线即可看出差异很明显，曲线重合度非常不好，均方误差为10-3数量级。从理论上说，这是由于α′n的分布并不是真正的均匀分布，事实上，它随N的增大而逼近[-π，π）上α′n的均匀分布。可见，当N较小时的均匀分布特性不理想，导致多普勒频移随机性较差，因此新模拟器统计特性与C S Xiao模拟器吻合程度很差，也就是说新模拟器精度较差。经多次仿真，随着N增大，新模拟器统计特性迅速逼近C S Xiao模拟器。图3、图4为N=100时新模拟器与C S Xiao模拟器统计特性对比。可以看到，当N=100时，新模拟器与C S Xiao模拟器统计特性重合度已很好，均方误差从10-3数量级降到了10-8，这个数量级的误差在信道模拟中是可接受的。因此，当N≥100时即可认为新模拟器与C S Xiao模拟器具有同样良好的统计特性。
　本文将查表法引入Rice信道模拟器的建模中，基于SOS模型和查表法设计了一种平坦Rice信道模拟器。该模拟器用查表法代替谐波运算，极大地减小了核心运算量，提高了模拟器的运行速度。为了避免查找表无限长，通过对模拟器数学模型的设计，适当弱化参量的随机性，使得查表法和SOS模型可以相容使用。最后通过仿真证实，虽然弱化了模拟器参量的随机性，但精度并未受到大的影响。均方误差表明新模拟器在精度上与未修改之前的模拟器相差甚小。在兼顾精度与速度的应用场合，新模拟器具有显著优势。
参考文献
[1] MATTHIAS P. Mobile fading chaimels[M]. NewYork： JohnWiley&Sons Ltd， 2002.
[2] AULIN T. A modified model for the fading signal at a mobile radio channel[J]. IEEE Transactions on Vehicular Technology， 1979， 28（3）：182-203.
[3] YIP K W， NG T S. Discrete-time model for digital communications over a frequency-selective Rician fading WSSUS channel[J]. IEE Proceedings Communications， 1996，143（1）：37-42.
[4] MATTHAIS P， KILLAT U， LAVE F， et al. On the statistical properties of deterministic simulation models for mobile fading channels[J]. IEEE Transactions on Vehicular Technology， 1998，47（1）：254-269.
[5] Xiao Chengshan， ZHENG R Y， BEAULIEU N C. Novel sum-of-sinusoids simulation models for Rayleigh and Rician fading channels[J]. IEEE Transaction on Wireless Communications， 2006， 5（12）：3667-3679.