聚类数" title="最佳聚类数" target="_blank">最佳聚类数的判定通常采用一种基于迭代的trial-and-error过程[1]进行，该过程是在给定的数据集上，使用不同的参数（通常是聚类数k）,运行特定的聚类算法,对数据集进行不同的划分，然后计算每种划分的指标值。通过比较各个指标值，其中符合预定条件的指标值所对应的聚类个数被认为是最佳的聚类数。实际上，trial-and-error过程存在两个不足之处:(1)聚类数k值的确定对于缺乏丰富聚类分析经验的用户来说是难以准确确定的[2]，这需进一步提出寻找更合理的聚类数k的方法; (2)目前提出的许多检验聚类有效性的指标，如Vxie指标[3]、Vwsj指标[1]等，但这些指标都是基于某个特定聚类算法提出的，在实际应用中受到了极大限制。鉴于上述两种情况，本文借鉴层次聚类的思想一次性地生成所有可能的聚类划分，并计算其对应的有效性指标，然后选择指标值最小的聚类划分来估计数据集的最佳聚类数，这样可以避免对大型数据集的反复聚类，而且该过程不依赖于特定的聚类算法。

1 聚类有效性指标
    本文采用的是一个不依赖于具体算法的有效性指标Q(C)来评估数据集的聚类效果。该有效性指标主要是通过类内数据对象的紧凑度以及类间数据对象的分离度[4]衡量聚类质量。


1.3 噪声点与孤立点的消除
    基于数据集中存在的噪声点与孤立点对聚类结果的影响，本文认为单独利用有效性指标所得出的聚类数为最佳聚类数k*的结论并不成立。根据参考文献[4-6]，采用基于MDL(Minimal Description Length)的剪枝方法对结果进行处理。具体处理方法如下：

    两个数据对象样本间的相似系数等于d个属性间相似系数之和，每对属性间的相似系数等于每对属性的曼哈顿距离加1的倒数。式(9)把两个数据对象间的每个属性的相似系数都映射到(0,1)的区间,可以得到,当s(xi,xj)的值越大，则数据对象xi和xj越相似。
2.2 最佳聚类数确定算法(COBH)
    本文介绍的最佳聚类数确定算法(COBH)主要是借鉴层次聚类的思想。该算法是在初始化时，使得数据集的聚类个数k为数据对象的个数n，再根据式(9)计算数据集中的任意两个数据对象的相似度s(i,j)，并将它们存储在一个一维数组D中,将数组D的元素从大到小排序；对数组D中的当前元素，首先判断这两个数据对象是否已被合并到类中,如果没有，则将这两个数据对象合并成一个类，如果其中一个数据对象已被合并到某一个类中，则将另一个对象也合并到那个类中；如果它们已分别被合并到两个不同的类，则将它们所在的那两个类合并成一个类，如果它们已经属于同一个类，则放弃此次合并。此时，根据式(6)计算聚类有效性指标Q(C)的值，连同此时的聚类划分情况一起保存在数组A中，此时数据集的聚类个数k=k-1；然后取D中的下一个元素继续进行判断与计算，直到数据集的聚类个数为1时结束；根据获取数组A中最小的聚类指标值以及所对应的聚类划分；将所选择的最小聚类指标值以及所对应的聚类划分情况，按式(7)的过程对其中被识别为噪声点与孤立点所组成的类进行剔除，最后获得最佳的聚类数kopt,并且得到该算法的时间复杂度为O(n2)。
3 实验与分析
     为了验证COBH算法的性能与有效性。本文选用5个数据集，分别来自人工合成与UCI的标准数据集库。为了验证该算法所采用的有效性指标在进行运算时具有较高的效率与性能，本文选择了基于数据样本几何结构的两种具有代表意义的指标Vxie[3]和Vwsj[1]作对比,这两种指标都是基于FCM聚类算法。并选择新近提出基于层次划分的最佳聚类数确定算法(COPS)也做为对比对象。
     实验所使用的PC机为CPU 2.80 GHz,内存为2 GB，算法采用VC6.0进行实现。
3.1数据集的选择
    第一类数据集是人工合成的数据集。实验采用2个人工合成的数据集，分别为数据集DB1和DB2。数据集DB1由中心分别为(0,0)和(40,40)的二维高斯分布数据对象组成，数据样本均为400个。主要特征是两个聚类之间属性差别比较大。数据集DB2是以(0,0)、(40,40)和(60,60)为中心点的人工合成的数据集，它是一个二维三个类的数据集，其主要结构特征为轻微重叠、松散的、和带有少量噪声点的聚类结构。
   第二类数据集为标准数据集。本实验采用3个来自UCI的标准数据集，分别是IRIS、Wiconsin breast cancer和Vowel recognition。在本文中的数据集代号分别表示为DB3、DB4和DB5。
3.2实验结果
    本次实验分两组进行，第一组是验证算法COBH在数据集的最佳聚类数确定方面的有效性。分别运行所选择的5个数据集得到的聚类数与有效性指标值的关系，如图1所示。

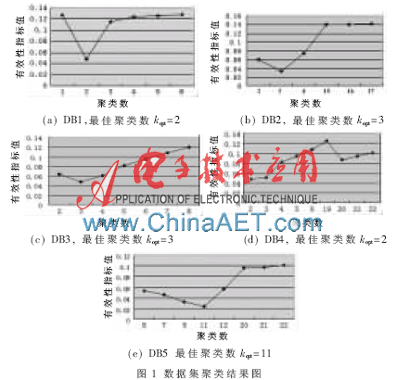
    由图1得出,由于数据集中的数据对象分布以及几何结构不同，算法COBH对数据集处理效果也有所不同。对于数据集DB1，由于该数据集是在合成过程中保持了类与类之间较大的差异性，而且分布比较集中、几何结构比较标准，所以该方法通过处理得到的指标值能更好地反应出最佳聚类数，如图1(a)所示。当聚类数为2时所对应的有效性指标值与其他指标值差别比较明显，而且此时其有效性指标最小。对于数据集DB2，由于其存在噪声点，所以在刚开始时，其指标值变化特别明显，然而当聚类数达到15以上时，指标值变化趋于平稳，如图1(b)所示。对于数据集DB3，由于其数据对象个数比较少，而且还包含两个重叠的簇，算法也能得到准确的结果，说明该算法能够有效地区分重叠的簇,如图1(c)所示。数据集DB4如图1(d)所示，当其聚类数由3降到2时,其有效性指标值差异很小，但算法COBH也能够做出正确的区分。而对于数据集维数比较高的DB5，该算法能够识别出正确的聚类数，而当聚类个数达到20时,其有效性指标值逐渐趋近于平稳，说明算法COBH对数据集DB5处理的结果比较优良,如图1(e)所示。
    第二组主要是验证算法COBH的性能与时间效率。本文采用参考文献[1,3]中基于FCM算法的有效性指标Vxie和Vwsj作为对比对象。在实验中，设置FCM聚类算法的模糊因子m为2;另外本文也选择参考文献[4]所提出的COPS算法作为对比,不同算法所获得的最佳聚类数情况如表1所示。在实验中，每个数据集要在每个算法中运行多次并记录每次运行时间，取这些时间的平均值作为该算法处理该数据集所用的时间，如表2所示。

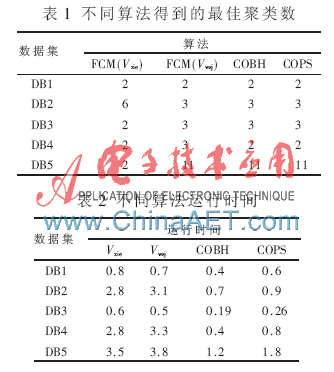
    由表2可以得出，对于结构比较标准、分布比较集中的数据集DB1，4种算法运行的时间几乎相似。而当数据集的个数、维度不断增加时，算法COBH和COPS表现的效率更佳。特别当数据对象的维度较高时，算法COBH的效率会更高，且在时间上要比其他算法快。COPS算法首先确定单个维度上的相似数据对象，进而确定高维空间中的相似数据对象，其计算量比较大。而算法COBH则是通过新的相似判定方法将数据对象从整体进行相似性判定。所以随着数据对象的维数增加，其效率明显提高。
    通常确定数据集的最佳聚类数的方法，一般需要用户根据先验知识提供准确的聚类数k并运行某个特定的算法，这样就使其应用受到了限制。本文提出了新的确定数据集的最佳聚类数的算法(COBH)，该算法借鉴了层次算法的思想，弥补了传统算法的缺点，同时能获得较好的聚类结果。理论研究和实验结果证明,本文所提出的算法具有良好的性能及较高的时间效率。
参考文献
[1] SUN H, WANG S, JIANG Q. FCM-Based model selection algorithms for determining the number of cluster[J].Pattern Recognition, 2004,37(10):2027-2037.
[2] 周世兵.新的k-均值算法最佳聚类数确定方法[J]. 计算机工程与应用, 2010,46(16):27-31.
[3] XIE X,BENI G. A validity measure for fuzzy clustering[J].IEEE Trans, on Pattern Analysis and Machine Intelligence, 1991,13(8):841-847.
[4] 陈黎飞,姜青山,王声瑞. 基于层次划分的最佳聚类数确定方法[J]. 软件学报, 2008,19(1):62-72.
[5]     FOSS A, ZAIANE O R. A parameterless method for efficiently discovering clusters of arbitrary shape in large data sets[C]. Proc. of the ICDM, Los Alamitos: IEEE Computer Society Press, 2002.
[6] AGRAWAL R, GEHRKE J, GUNOPULOS D, et al. Automate subspace clustering of high dimensional data[J]. Data Mining and Knowledge Discovery, 2005,11(1):5-33.
[7] 孟佳娜,邓俐伶,等.一种改进的k均值聚类算法[J].大连民族学院学报,2011,13(3):274-276.