摘 要: 介绍了局部线性嵌套和等距映射两种最基本的非线性降维方法,对比测试了两种降维方法在不同参数下的执行效果与效率,总结了两种降维方法所适合的数据特点,并应用于图像识别中,比较了两者在图像识别中的识别率。
关键词: 非线性降维;流形学习; 局部线性嵌套; 等距映射; 人脸识别
流形的概念最早是由德国数学家黎曼在1854年提出的,它是微分几何学的基础[1]。流形本质上是局部可坐标化的拓扑空间,可以看作是欧式空间的非线性推广。
1 局部线性嵌入算法
局部线性嵌入算法LLE(Locally Linear Embedding)是ROWEIS S T和SAUL L K于2000年提出的一种非线性降维方法[2],该方法主要认为在局部意义下,数据结构是线性的,或者说局部意义下的点是在一个超平面上,故可以使用任意一点的邻近点的线性组合来表示该点。对于一组具有嵌套流形的数据集,在嵌套空间与内在低维空间局部邻域间的点的关系应该保持不变。即在嵌套空间,每个采样点可以用它的近邻点线性表示,在低维空间中保持每个邻域中的权值不变,重构原数据使重构误差最小。
通过最小化这种线性表示的误差,可以建立如下数学模型:
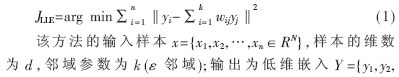

该算法有两个待定的参数k和d,由于重构成本函数同时最小化得到的最优权值应该遵循对称性,因此每个点的邻近权值在进行平移、伸缩和旋转变换时保持不变[3]。
2 等距映射
等距映射算法是由TENENBAUM J B等人于2000年提出的一种非线性降维方法[4]。该方法试图保持数据内部几何特征,从而获得流形上数据之间的测地距离。与传统的非线性降维方法所不同的是,利用等距映射方法可以求得高维数据的本征维数,将本征维数较低的高维数据投影到低维空间中去[5],使得高维数据可以直接观察。等距映射有两个假设:(1)高维数据所在的低维流形与欧式空间的一个子集是整体等距的; (2)与数据所在的流形等距的欧式空间的子集是一个凸集。
实验3
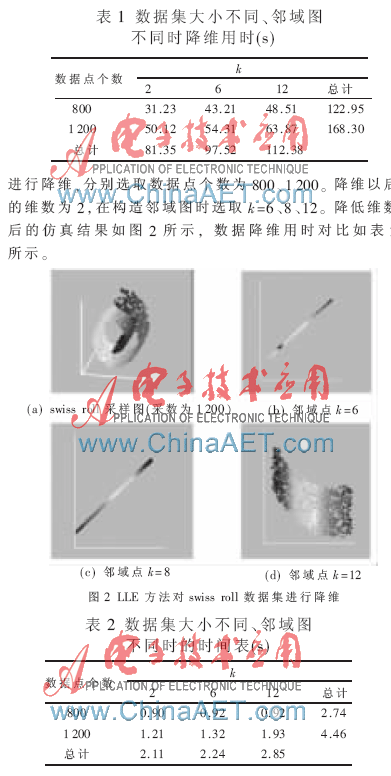
使用MATLAB软件用siomap方法对scurve数据集进行数据降维,分别选择数据点个数为800、1 200,降维以后的维数为2,在构造邻域图时选取k=2、6、12。降低维数后的仿真结果如图3所示, 数据降维用时对比如表3所示。
实验4
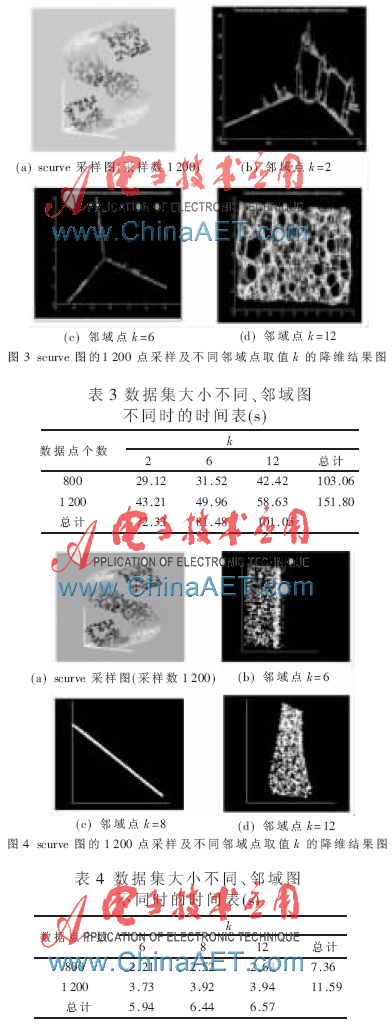
使用MATLAB软件用LLE方法对scurve数据集进行降维,分别选择数据点个数为800、1 200,降维后的维数为2,在构造邻域图时选取k=6、8、12。降低维数后的仿真结果如图4所示,数据降维用时对比如表4所示。
4 结果分析
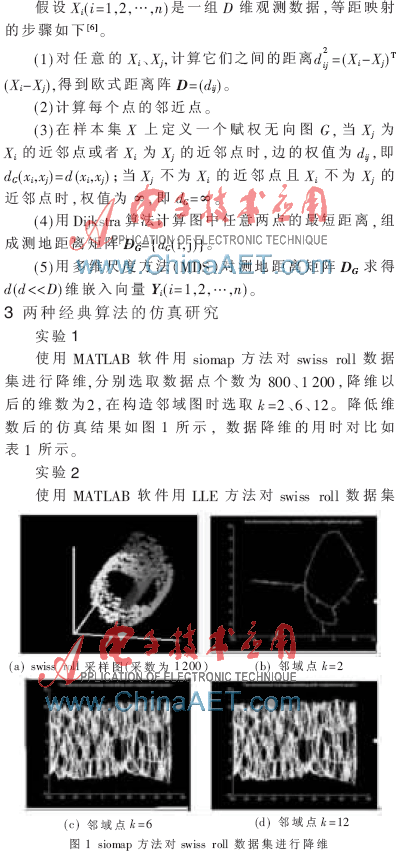
实验1中,从图1可以看出样本点的分布及其邻域点的取值对isomap的降维结果会产生比较大的影响[7]。实验2中,随着邻域点k取值的增加,图2有着明显的变化,说明随着邻域k的增加,LLE所得的结果明显增强。在样本点稀疏的情况下,邻域k的取值对于LLE降维效果有比较明显的影响,因而选取合适的邻域取值对于LLE降维有非常重要的作用。对比实验2和实验4可知,邻域k的选择对于不同数据集的选取是不同的。LLE算法中的待定参数很少(k和d),从图3可以看出,随着样本邻域选取的增加,会把其他较远点一起纳入,从而造成结果的误差,说明邻域的选取对于实验有着直接的影响。
通过对比实验运行的时间会发现,isomap所用时间远远大于LLE。其中主要原因是计算欧式距离矩阵花费时间比较长,计算赋权无向图运算量比较庞大,用多维尺度方法(MDS)时会用到大量的矩阵运算,对于每一个不同的数据集,需要重新计算距离矩阵等,算法复杂度比较高,而LLE运算量相对较少。
isomap算法计算图上两点间的最短距离, 执行起来比较慢,该方法适用于学习内部平坦的低维流形, 不适于学习有较大内在曲率的流形。LLE算法可以学习任意维数的低维流形,每个点的近邻权值在平移、旋转和伸缩变换下是保持不变的。在计算耗时上,isomap远远大于LLE。
参考文献
[1] 王泽杰.两类非线性降维流形学习算法的比较分析[J].上海工程技术大学学报,2008,22(1):54-59.
[2] ROWEIS S T, SAUL L K. Nonlinear dimensionality reducation by locally linear embedding[J]. Science,2000,26(8): 2323-2326.
[3] 赵连伟,罗四维,赵艳敞.高维数据的低维嵌入及嵌入维数研究[J].软件学报,2005,12(8):1423-1430.
[4] REINHARD K,NIRANJAN M. Subspace models for speech transitions using principal curves[J].Proceedings of Institute of Acoustics,1998:53-60
[5] 王靖.流形学习的理论与方法研究[D].杭州:浙江大学, 2006.
[6] 孙明明.流形学习理论与算法研究[D].南京:南京理工大学, 2007.
[7] 刘小明.数据降维及分类中的流形学习研究[D].杭州:浙江大学,2007.

