摘 要: 通过分析光谱信号特征,结合稀疏表示理论,提出了一种自适应稀疏表示的光谱去噪方法。该方法对信号分段构造学习样本,分别用OMP法和K-SVD法初始化和过训练原子库。将光谱信号在新的原子库上进行自适应稀疏分解,实现光谱信号去噪。利用信噪比(SNR)、均方根误差(RMSE)、波形相似度(NCC)、峰值平均相对误差(AREPV)四个指标来评价去噪效果。仿真实验结果表明,与小波软阈值和小波硬阈值方法相比,该方法能更好地同时消除噪声和基线漂移。
关键词: 光谱预处理;自适应稀疏表示;去噪;基线校正
红外光谱技术在农业、医疗、航天和环境监测等领域得到了广泛的应用。在光谱获取的过程中,不可避免地存在噪声和基线漂移[1]。因此,光谱去噪和基线校正是光谱预处理的关键步骤。目前有很多光谱预处理方法,Donoho[2]提出了小波阈值去噪,该方法包括小波分解、分解稀疏的阈值处理和信号的小波重构。刘艳萍等[3]提出提升小波变换和中值滤波结合的红外光谱去噪,将一种光滑阈值函数和一种分层阈值选取方法相结合对光谱信号去噪,并对提升小波重构信号进行中值滤波。方勇华等人[4]将光谱信号低频段小波系数置零,以实现基线校正,通过对高频段小波系数阈值处理来实现去噪。但是,小波阈值处理的有效性是以信号小波表示的稀疏性为前提,即只有信号与小波基存在相关性时,才能获得信号的稀疏表示。因此,选用阈值处理消除噪声时,很多情况下也会损失光谱信号中的有特征信息。
信号的稀疏表示方法是近年来信号处理的研究热点。稀疏表示去噪就是不断地跟踪并提取最能匹配于原始信号及其残差信号的原子向量的过程[5]。稀疏分解是获取信号稀疏表示的有效途径,在一定程度上克服了小波阈值降噪的缺点[6]。但是,常用的稀疏分解依赖特定原子库,不具普适性。本文基于光谱信号的特征信息和噪声之间的弱相关特点,提出自适应稀疏表示的光谱去噪和基线校正方法。


(3)将分段的信号去噪后,对存在重叠部分进行均值处理。合并每段信号,依据信号不同的重叠程度,再对合并后的信号进行平滑滤波处理,实现整个光谱信号的去噪。
2.2 光谱基线校正
光谱的基线干扰主要存在低频段,近年来,用于基线校正的方法有正交投影法、傅里叶变换法和小波变换法等,以上各种方法都有各自的局限性。其中,小波在基线校正的效果较好,但小波变换是一种基函数固定的表示方法,当实测不同物质的光谱信号时必须重新选择小波基的问题,因此在工程应用中效果较差。
本文采用更为精确的稀疏表示方法来求得函数的基线,具体做法如下:
(1)设f0(k)为去噪后的光谱;
(2)将f0(k)分为高频和低频两部分,低频部分又可相对分为高频和低频部分,与稀疏去噪的迭代算法类似,多次迭代直到光谱的基线几乎不改变,则算法终止。
3 仿真实验与结果讨论
3.1 实验数据[3]
本文采用仿真的纯光谱信号,长度取L=1 024;噪声信号采用信噪比为20 dB的加性高斯白噪声,原始图和加噪后的光谱信号如图1所示。基线信号采用多项式y=anxn+an-1xn-1+…+a2x2+a1x+a0来模拟,同时含有噪声和基线漂移的仿真光谱信号如图2所示。光谱信号去噪的目的是尽可能多地消除光谱的噪声,同时又要保留有用的光谱信息。因此消噪后的光谱信号信噪比越高,与原信号的均方误差越小。波形相似度越接近1,波峰值越接近原始光谱,则去噪后的光谱越接近于原始的光谱信号,去噪效果就越好。


从图3和表1可以看出,小波阈值法虽然可以有效地去除光谱信号高频噪声,但该方法同时也滤除了一些有用信息;稀疏表示较小波阈值法有更好的去噪效果。本文算法在去噪的同时,较好地保留有用信息。因此本文方法更适合光谱信号去噪。
3.3 光谱去噪和基线校正
对于同时含有噪声和基线漂移的信号,分别比较几种方法对光谱信号去噪和基线校正果对比,如图4和表2所示。
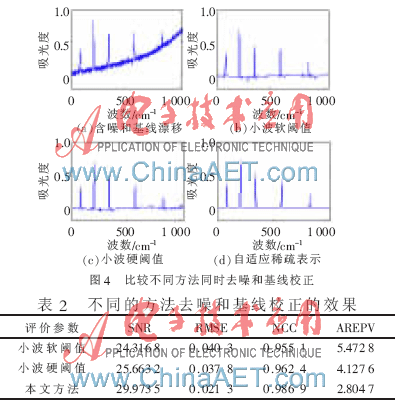
从图4和表2可以看出,在同时含有噪声和基线漂移的光谱信号时,小波软阈值和硬阈值方法也可基本以实现去噪和基线校正,但在含噪幅度较大处仍然有一些噪声残留,基线校正不彻底,本文方法能较好地实现去噪和去基线。
依据信号超完备稀疏表示理论,分析光谱信号的噪声和特征信息之间弱相关的特点,本文提出自适应稀疏表示的光谱去噪方法。针对光谱信号数据量大,对光谱信号分段,并进行去噪和基线校正,再进行组合平滑滤波,有效地实现整个光谱去噪和基线校正。仿真实验结果表明,与小波软阈值法和硬阈值方法对比,本文方法可以获得更高的评价参数,有效地提高了光谱信号预处理效果。
参考文献
[1] 刘志宏,邓波,周玉荣,等.红外光谱预处理中去噪的研究[J].光谱实验室,2006,23(4):815.
[2] DONOHO D L. Denoising by soft threshold[J]. IEEE Transactions on Information Theory, 1995,41(3):613-627.
[3] 刘艳萍,高国荣,龚宁,等.提升小波变换和中值滤波结合的红外光谱消噪[J].光谱学与光谱分析,2012,32(8):2085-2088.
[4] 方勇华,孔超,兰天鸽,等.应用小波变换实现光谱的噪声去除和基线校正[J].光学精密工程,2006,14(6):1088-1092.
[5] 王建英,尹忠科,张春梅.信号与图像的稀疏分解及初步应用[M].成都:西南交通大学出版社,2006.
[6] 肖泉,丁兴号,王守觉,等.基于自适应超完备表示的图像去噪方法[J].仪器仪表学报,2009,30(12):1886-1890.
[7] CAND E J, ROMBERG S J,TAO T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information, IEEE Trans. Inform. Theory, 2006, 52(2):489-509.
[8] DONOHO D L, Compressed sensing[J]. IEEE Trans. Inform. Theory, 2006, 52(4):1289-1306.
[9] AHARON M, ELAD M, BRUCKSTEIN A M, et al. K-SVD: An algorithm for denosing over-complete dictionaries for sparse representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311-4322.

