摘 要: 由于蓄电池机理复杂,蓄电池的温度具有明显的非线性、滞后性和模型不确定性,采用BP神经网络对蓄电池温度进行仿真研究,建立网络模型,反映蓄电池温度变化趋势。
关键词: BP算法;神经网络;蓄电池;温度;模型
蓄电池的温度变化是一个复杂的、多变量相互影响的过程,不仅受环境因素影响,还与充放电时间、充放电电流、内阻大小、使用寿命等有关。蓄电池温度与各因素之间存在非线性关系,很难用数学解析的方式建立准确的模型[1-2]。
蓄电池的温度值直接影响到电池容量,可以根据蓄电池的使用寿命、工作状态、运行时间估算出蓄电池的温度和电池剩余容量,为蓄电池做出可行的预判,因此掌握蓄电池的温度值是很重要的。本文采用神经网络建模的方法模拟蓄电池温度,为使用者提供比较准确的参考[3]。
根据蓄电池物理特性的要求,电池的充电和放电不能同时进行,否则会损害电池性能,造成不可挽回的损坏。电池充电时温度值变化呈现一定的趋势,前期大电流充电制,由于充电电流很大,蓄电池内阻产生的热量加上电池电化学反应产生的热量,使温度急剧升高;随着充电时间的增加,充电电流变小,内阻产生的热量随之减少,蓄电池与外部环境交换热量的增加,致使蓄电池温度出现下降的现象。蓄电池放电时温度变化呈现不规则趋势,这主要与蓄电池的工作状态、放电制要求有关,当采用大电流放电制时,蓄电池内阻产生的热量会大于电池电化学反应吸收的热量,电池温度持续上升;当蓄电池采用的工况改变,放电制电流减小时,电池电化学反应的吸热会大于内阻产生的热量,电池温度又会下降[4]。
由此可见,蓄电池的充放电过程温度变化极其不规则,温度值的改变受各种因素的影响,要想建立准确的数学模型具有很大的困难,因此本文以实验数据为基础,建立神经网络模型,并进行仿真研究,时时了解蓄电池温度情况,为蓄电池的工作提供必要的信息。
1 前馈型神经网络模型
前馈型网络包含输入层、隐含层和输出层。通常网络有一个或多个隐含层,隐含层的神经元数量由训练效果来确定。输入层可以看做是缓冲器,没有处理功能。隐含层的非线性传递函数神经元可以学习输入输出之间的线性和非线性关系,进行权值处理。输出层的作用是拓宽网络输出。图1所示为具有单隐含层的BP网络模型。
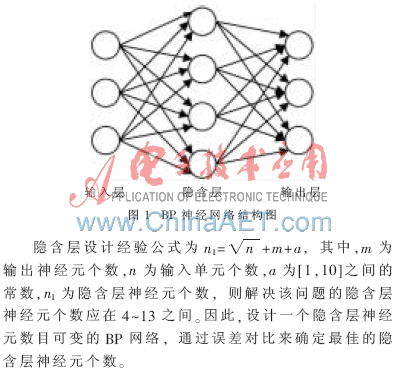
在确定了神经网络结构后,通过输入和输出样本集对网络进行训练,即对网络的阈值和权值进行学习和修正,使网络实现给定的输入输出映射关系。其学习分为两个阶段:
(1)输入已知的学习样本,通过设置网络结构和前一次迭代的权值和阈值,从网络的第一层向后计算各神经元的输出;
(2)对权值和阈值进行修改。从最后一层向前计算各权值和阈值对总误差的影响(梯度),据此对各权值和阈值进行修改。以上两个过程反复交替,直到达到收敛为止。
2 Levernberg-Marquart算法
标准的BP算法是一种梯度下降的学习算法,其权值的修正是沿着误差性能函数梯度的反方向进行的,其主要不足是训练时间较长。相应的有许多加速收敛技术,如变量BP算法、变梯度算法、拟牛顿算法、LM算法等。
通常对于权值数较少的用于逼近函数的神经网络,LM算法的收敛速度较快。如果要求的精度比较高,则该算法的优点尤其突出,采用LM算法可以获得比其他算法更小的均方误差。其具体计算步骤如下:
(1)将所有输入提交网络并计算相应的网络输出和误差;
(2)计算雅克比矩阵;
(3)求取误差?驻xk;
(4)用xk+?驻xk重复计算平方误差之和,当平方误差之和小于某个目标值时,认为算法收敛。
3 蓄电池充电模型
蓄电池采用4阶段充电制,当到达过渡电压时本阶段充电电流就转为下一阶段的充电电流,顺序为2 400 A—1 200 A—600 A—300 A[5]。
根据前面的分析确定神经网络采用三层模型结构,输入层3个输入量:充电时间、充电制和电解液密度;输出层1个输出量:蓄电池温度;隐含层的神经元数量定为5个(后续网络建立,训练数据时,发现选用5个中间节点的隐含层,网络训练的效果最佳,数据拟合程度最高)。表1为训练网络用的部分实验数据;表2为充电时电解液密度的变化数据。


蓄电池的电解液密度变化与温度、放电历史互为影响,但影响效果有限,同一时刻不同组的密度数据仅相差0.02 g/cm3。
图2所示为BP神经网络模型模拟的充电温度变化曲线图。图3为充电仿真步数精度曲线图,从图中可以看出训练精度可达10-3。图4为预测数据拟合图,从中可以看出,预测数据与测量值的误差不超过1 ℃,原因是用于训练网络的实验数据量比较小,造成了局部时间内误差偏大,如果采用大量的实验数据进行仿真,则能得到更理想的效果。

4 蓄电池放电模型
蓄电池温度并非随时间的增加而上升,在长时放电的情况下(50 h和20 h放电制),蓄电池温度是逐步降低的,而在短时放电时(5 h、1 h以及0.5 h放电制),蓄电池温度是逐渐上升的[5]。图5和图6分别为长时和短时放电情况下电解液温度变化曲线。

蓄电池内阻在放电过程中随着放电电流、放电时间而变化。在内阻变化不是很大的情况下,内阻产生的热量(Q=I2R)主要取决于放电电流。
表3所示为在不同放电制下蓄电池内阻随放电时间的变化情况,从中可以看出,当大电流放电时,蓄电池的内阻是逐渐减小的;而当小电流放电时,长时间放电使蓄电池电动势降低,电池内阻逐渐增大。
蓄电池长时放电时,电化学吸收的热量大于内阻放出的热量,以至蓄电池的温度保持下降,短时放电时电化学吸收的热量小于内阻放出的热量,造成蓄电池的温度变化与长时放电时正好相反。蓄电池放电温度模型输入层采用3个输入量:放电制、放电时间和电解液内阻;输出层采用1个变量:蓄电池温度;隐含层选用5个元素作为中间节点。
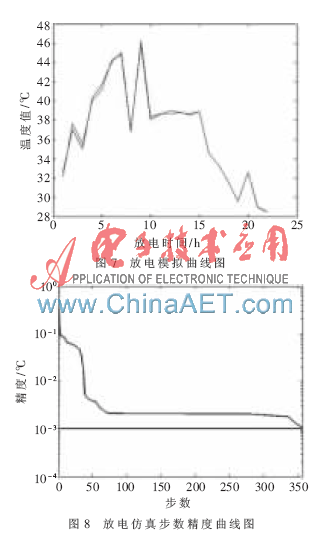
图7为放电模拟曲线图,图8为放电仿真步数精度曲线图,从图7和图8可以看出网络模拟的精度很高。图9是预测数据拟合图,从中可以看到,初始时刻温度预测数据与测量值的误差很大,造成这种情况的主要原因是开始时刻温度值变化大,变化速度快,实验数据量比较小。
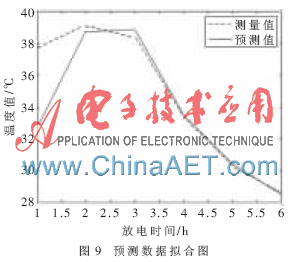
本文根据蓄电池的化学特性,影响蓄电池温度变化的因素,提出用BP神经网络建立蓄电池充放电时的温度模型。建立模型的预测值与实际测量值拟合程度较高,对时刻掌握蓄电池性能、温度数据等起到很大的辅助作用。
参考文献
[1] 黄晓辉,黄声华,万山明.基于DSP的潜艇蓄电池分级恒流充电控制系统研究[J].船电技术,2007,27(6):329-333.
[2] 毕恩利,朱华兵.基于某型潜艇蓄电池组巡检系统设计[J].机电工程技术,2007,36(3):28-30.
[3] 许亦峰,张荣昌.常规潜艇水下电量消耗建模与仿真[J].青岛大学学报,2008,21(2):43-46.
[4] 马守军,庄亚平,陈新传.潜艇蓄电池建模策略分析[J].船电技术,2004,24(4):23-25.
[5] 徐鲁杰,刘镇.潜艇用新型铅酸蓄电池万用放电模型研究[J].武汉理工大学学报,2009,33(1):177-179.

