因此这里要引入一个重参数,重要程度堪比增益带宽积。那就是运放的全功率带宽。虽然只是一个数学推导。
Vout = Vp * sin(2*pi*f*t)
这个输出电压对时间求导可得:
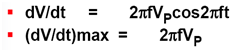
上式的max是指在求导后的余弦信号在t=0时得到最大值。这个很好理解,也就是说原正弦信号在t=0时压摆率最大。
可以看出dV/dt表示的压摆率,跟信号的频序有关,还与信号的输出幅值有关。上式中,如果Vp是运放的输出满幅值。则上式可表示为

此时FPBW就是运放的满功率带宽了。记住它吧,它简值太重要了。例如如果想在100Khz以内得到正弦波的10Vo-p振幅,按照公式需要转换速率的是6.3v/us以上的OP。可以看出,满功率带宽由压摆率和输出信号的幅值决定的。也就是压摆率一定的情况下,输出信号的幅值越大,全功率带宽越小。这也解释了上面OPA333的测试结果。
这里还要说一个得要的公式,就是运放的上升时间与带宽的关系。如下式,面熟,这个公式在很多地方都见过。也太重要了,记住它吧。
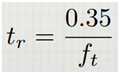
今天我们深一点分析这个公式的由来。其实它是由一阶系统的响应计算而来的。对于一阶RC的频率响应为
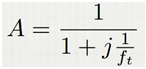
一阶系统的阶跃响应为下式。
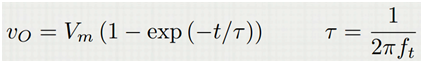
Vo=0.1Vm时 t=0.1RC。(-ln0.9 =0.1)当Vo=0.9Vm时,t=2.3RC (-ln0.1=2.3)。则RC阶跃 响应的时间为Tr=2.2RC.
而对于一个一阶RC的带宽又可以表示为:BW=1/(2*pi*RC)。上升时间里也有RC,这两个RC是同一个喽。这句是废话。那Tr=2.2/(2*pi* BW)=0.35/BW。
下面我们对这个结论用TINA进行一下仿真。运放为OPA2188,增益带宽积为2MHz。运放设置为增益为1的同向放大电路。输入信号为10mV的阶跃信号。输出信号的上升时间为220.8ns-82.5nS=138.3nS.
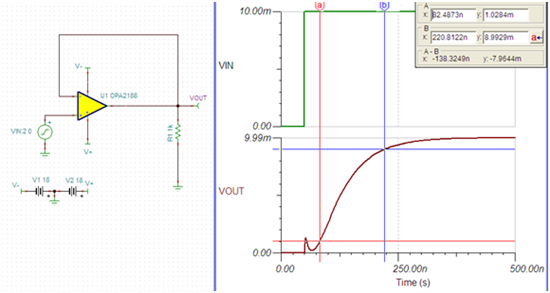
下面看一下计算结果:计算结果为175nS。约20%的误差。但也有很好的参考价值了。


