摘  要: 过分割是计算机视觉领域流行的图像预处理方法。针对其运行速度慢的缺点，对广泛采用的Turbopix算法提出CUDA并行优化的方法。通过每个线程执行一个超像素扩张的任务分配，实现了水平集函数的并行演化；利用纹理存储空间和常数存储空间的优化策略,改善了数据访存的效率。实验结果表明，在GT 240M平台上，平均加速比达到了15以上。
关键词: 过分割； 超像素； Turbopix； CUDA

     超像素是图像中局部区域内连通、亮度相近、边缘描述性较好的像素集合。将图像划分成超像素后，其图像单元更加符合人们期望的结构粒度[1]。由于能够更有效地表示图像结构， 超像素被广泛应用于图像内容标记[1]、虚拟漫游[2]、图像分割[3-6]等领域。将图像表示由像素转换成超像素的过程称为过分割(Over Segmentation)。常用的过分割算法有均值漂移[7]、分水岭[8]、N-Cuts[9]和Turbopix算法[10]。均值漂移和分水岭算法的优点是计算复杂度较低，缺点是平滑区域存在着严重的欠分割(Under Segmentation)现象。N-Cuts和Turbopix算法通过紧致性约束(Compactness Constraint)有效解决了该问题。N-Cuts综合考虑全局和局部信息，利用图论算法对图像内容进行划分。图像中的像素对应图的节点，像素间的邻域关系对应图的边，边的权重反映了相邻像素间的相似性。但是N-Cuts算法是NP难题。SHI J等人提出的谱估计算法[9]复杂度为O(N3/2)，其中N为像素数目。FEZENSZWALB P等人基于图节点聚类准则将N-Cuts算法的复杂度降为O(NlogN)[11]，但该方法不能控制生成的超像素数目。VEDALDI A等人在Mean-Shift的基础上提出了计算速度更快的Quick-Shift算法[12]; LUCCHI A等人提出了计算复杂度为O(N)的简单线性迭代聚类算法SILC(Simple Linear Iterative Clustering)[13]，但这两种方法在平滑区域都存在欠分割现象。在计算机视觉领域曲线演化算法[14-15]的启发下， LEVINSHEIN A等人提出的Turbopix算法[10]具有与N-Cuts算法同等或更优的性能，但显著降低了计算时间，其计算复杂度和像素数目近似成线性关系。Turbopix算法通过自适应局部结构的种子膨胀实现超像素的分割,其核心思路是将复杂的超像素分割难题简化为易解的几何流(Geometry Flow)问题。
    虽然Turbopix算法与N-Cuts算法相比计算速度有显著提高，但对于中等分辨率的图像，其计算时间仍需要十几秒。为了进一步提高过分割的计算速度，本文在分析Turbopix算法并行性的基础上，提出在GPU上CUDA并行实现的方法。
1 Turbopix算法分析
    Turbopix算法的基本思路是设计一个几何流,使得曲

　算法的具体计算步骤如下。
　(1)计算像素的局部相似性函数φ(x,y)及其梯度。
    (2)在图像I上均匀放置K个种子。
　(3)扰动种子位置，使其偏离梯度较大的区域，以避免初始阶段超像素边界扩张过慢。
　(4)有符号欧几里得距离函数ψ和分配值图A的初始化。A(x,y)若为非负值，则表示像素I(x,y)所属超像素的序号；否则表示未分配到任何超像素中。
   (5)统计演化前已分配的像素个数C1。
　(6)将演化时刻n初始为0。
　(7)超像素扩张：计算速度图SI和SB，根据式(2)更新ψ,并由ψ更新分配值图A。
　(8)统计演化后已分配的像素个数C2。
　(9)演化时刻n递增1。
　(10)判断终止条件：如果(C1-C2)／图像总的像素数>某个常数，将C2值赋给C1并跳到步骤(7)，否则跳到步骤(11)。
    (11)后处理：将未分配的像素划分到最邻近的超像素中。
    (12)从ψ中提取零水平集，作为超像素的边界。

2.6 后处理的CUDA优化
    当超像素边界扩张终止时，还有部分像素处于未分配状态。后处理就是将这些未分配的像素划分到距离其最近的超像素中。
2.7 超像素边界提取的CUDA优化
    超像素的边界为距离函数ψ的零水平集，1表示边界，0表示非边界。这实际上就是分配值图中非负值和负值之间的边界。
3 实验与结果讨论
    本文实验的硬件配置为Intel Core2 Duo 2.20 GHz CPU，2 GB内存；GeForce GT 240 M 1.21 GHz GPU，16 KB共享内存，436 MB全局内存。软件配置为Windows 7+Visual Studio 2008+CUDA SDK 4.0+NVIDIA Driver for Windows7(275.33)。
    将Turbopix算法的CPU实现[10]与本文的CUDA实现进行对比，测试图像为参考文献[10]提供的lizard。图1给出了在不同超像素个数下，本文CUDA优化实现的平均加速比。在该实验中，测试图像lizard的分辨率为518×344。从图1可以看出，经过CUDA优化后平均加速比达到了15以上。

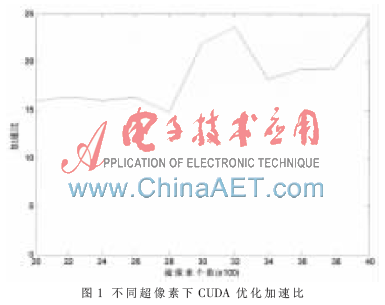
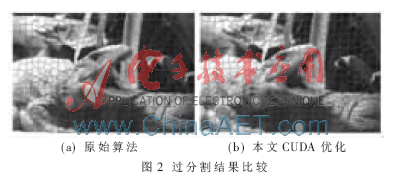
    图2给出了超像素个数为500时，原始算法[10]和本文CUDA优化得出的过分割结果。从图2可以看出，本文CUDA优化输出的结果与原始算法结果存在差异。原始算法过分割的结果更接近目标的边界，而本文优化的结果则在各超像素大小上更趋于一致。这种差异存在的主要原因是这两种实现的SB速度计算方法不一样。原始算法将位于未分配区域骨架处的所有像素点对应的SB设为0，其他区域处则设为1。本文为便于CUDA实现，根据分配值图确定SB的值。

    通过研究Turbopix算法的原理，本文提出了在GPU上高速并行实现的方法。该方法利用超像素边界扩张的数据独立性，提出了原始算法关键步骤CUDA并行优化的思路，并通过纹理存储器和常数存储器优化了内存访问的效率。未来工作是改进速度分量的计算方法，使本文实现结果与原始算法结果更加一致；进一步优化CUDA实现方式，使加速比能有更大的提高。
参考文献
[1] 刘靖，李翠华，杨敦旭. 一种基于超像素的户外建筑图像布局标定方法[J]. 厦门大学学报(自然科学版)，2010,49(2):175-180.
[2] 袁淑娟，高秀芬. 基于图像精确过分割的虚拟现实场景构建[J]. 计算机工程与设计，2009,30(17):4044-4046.
[3] 韩守东,赵勇，陶文兵,等. 基于高斯超像素的快速Graph Cuts图像分割方法[J]. 自动化学报，2011,37(1):11-20.
[4] 刘陈，李凤霞，张艳. 基于图割与泛形信息的对象分割方法[J]. 计算机辅助设计与图形学学报，2009,21(12):1753-1760.
[5] 方浩，仇丽英，卢嘉鹏. 基于区域划分和再融合的全幅视觉图像分割[J]. 北京理工大学学报，2009,29(9):799-802.
[6] 刘陈，王欣欣，李凤霞,等. 一种快速保边的图像对象分割方法[J]. 北京理工大学学报，2010,30(2):183-187.
[7] COMANICIU D, MEER P. Mean shift: a robust approach  toward feature space analysis[J]. IEEE Transactions on Pattern  Analysis and Machine Intelligence, 2002,24(5): 603-619.
[8] VINCENT L, SOILLE P. Watersheds in digital spaces: an efficient algorithm based on immersion simulations[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1991,13(6):583-598.
[9] SHI J,MALIK J. Normalized cuts and image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000,22(8):888-905.
[10] LEVINSHTEIN A, STERE A, KUTULAKOS K N, et al. TurboPixels: fast superpixels using geometric flows[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009,31(12):2290-2297.
[11] FELZENSZWALB P,HUTTENLOCHER D. Efficient graphbased image segmentation[J].International Journal of Computer Vision, 2004(1):167-181.
[12] VEDALDI A, SOATTO S. Quick shift and kernel methods for mode seeking[C]. Proceedings of the 10th European Conference on Computer Vision, Marseille, France, 2008:705-718.
[13] LUCCHI A, SMITH K, ACHANTA R. A fully automated approach to segmentation of irregularly shaped cellular  structures in EM images[C]. Proceedings of the International Conference on Medical Image Computing and Computer Assisted Intervention, Beijing, China, 2010:20-24.
[14] CASELLES V, CATTE F, COLL T, et al. A geometric model for active contours in image processing[J]. Numerische Mathematik, 1993,66(1):1-31.
[15] MALLADI R, SETHIAN J, VEMURI B. Shape modeling with front propagation:a level set approach[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1995,17(2): 158-175.
[16] 张舒,禇艳利,赵开勇,等.GPU高性能计算之CUDA[M].北京：中国水利水电出版社, 2009.