摘  要： 使用Xilinx公司最新生产的Spartan-6系列FPGA芯片，采用自顶而下的方法成功设计出一种基于LMS算法的横向自适应滤波器，并且通过了仿真检验，到达了设计目标,能实现预期功能。
关键词： 适应滤波器； LMS算法； FPGA； 横向结构

     有关自适应信号的研究是电子通信领域的重要课题之一，相关的理论和技术一直受到业界的高度关注。而自适应滤波器可以根据环境的改变，使用自适应算法来改变自身的结构和相关参数，是实现自适应滤波的有效途径。
    自适应滤波器的系数并不是预先设定好的，它是根据所采用的算法，利用从环境提取出来的参量和预设的目标值计算出来的。因而，它的参数并不是一成不变的，而是随着外界条件的改变而改变，并且能够跟踪输入信号的时变特征。然而，目前市场上的滤波器很多还是基于传统的集成电路设计方法，设计周期长，调试困难，而FPGA正是解决这一问题的有效途径。鉴于此，在深入研究自适应滤波器理论的基础上，通过FPGA来实现自适应滤波器具有很大的实际意义。
    本文通过对自适应滤波器理论的深入研究，基于最小均方误差(LMS)算法，采用自顶向下的FPGA设计理念，使用Xilinx公司最新生产的Spartan-6系列FPGA芯片，实现一种横向自适应滤波器,并且通过Matlab和Quartus II进行仿真和测试，验证了方案的正确性。该设计具有很强的创新性和社会应用价值。
1 自适应滤波器设计原理
1.1 横向自适应滤波器
    自适应滤波器的结构多种多样，本设计采用抽头延迟线模式的横向滤波器。这种结构层次十分清晰，并且在量化生产时降低了芯片的制作难度，从而节约成本，所以得到了广泛的应用。其结构如图1所示。

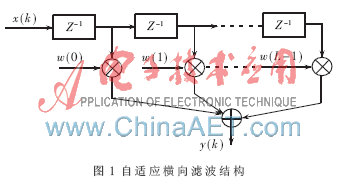
    权系数的调节过程简单来说就是不断将输出信号与所要得到的信号进行对比，根据两者之间的差异调整滤波器的系数，不断缩小两者间的差距，最后实现理想的输出状况。在横向滤波器中，系数体现在抽头的加权上，而加权系数就是系统根据自适应算法算出的，往复循环，直到达到理想输出。
1.2 LMS算法
　　由Professor Widrow和Dr. Hoff引入的最小均方(LMS)算法，由于其简单性、运算高效性和各种运行条件下良好的性能而被广泛应用。本文以此算法作为自适应滤波器的理论设计基础。
　　基于梯度的最小均方(LMS)算法是一种比较基础却很实用的算法。根据参考文献[1],当选定均方误差为权矢量二次函数时，性能度量曲线可以形象地看成是一个碗形曲面，这样自适应处理器的任务便是不断地向最低点逼近，即可以通过计算梯度的方法实现性能度量的最优化。其原理框图如图2所示。

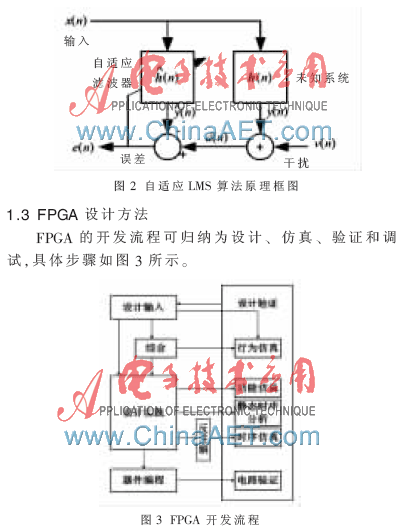
　    FPGA的设计方法有很多，本文采用的是较为流行的自顶而下的设计方法，如图4所示。采用此方法优点有很多。由于系统从上向下进行开发，所以在开发的过程中就可以进行适当的调试，而不是等到基本成型之后才寻找问题。这样可以尽早发现问题，减少研发中由于失误带来的损失。此外，由于底层设计会因顶层的变化而改变，所以修改的过程也变得更加方便。许多在设计过程中的新想法也可以加入到产品中试验，进一步提高性能。由此可见，本文所采用的设计方法是科学的、高效的。

2 基于FPGA的滤波器设计
2.1主要组成模块
　　本文用Xilinx公司最新生产的Spartan-6系列FPGA芯片进行自适应滤波器的设计。根据LMS算法计算过程实现的功能[2], 将自适应滤波器主要分为FIR滤波器模块、误差计算模块、权值更新模块、权值存储模块和控制模块。综合设计框图如图5所示。

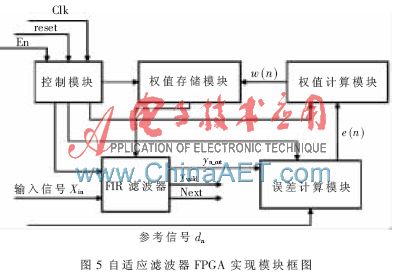
　    在该设计中,关于滤波器的部分,采用嵌入Matlab模块的方法，直接根据滤波原理构建模型。输入信号的延时和控制模块的实现使用Verilog语言编程。
2.2 控制模块
    控制模块主要用于初始化各模块、产生控制信号、控制各模块的特定功能、负责数据存储地址分配及数据输入/输出控制功能、根据外部输入的帧时钟生成数据存储模块以读取数据的读写地址等[3]。控制模块还要能够使系统的模块之间相互协调，保障系统在局部以及整体上工作流畅。
2.3 FIR滤波模块
    FIR滤波模块实现FIR算法和抽头系数调整。FIR算法得到Y(n),其主要实现一个卷积运算, 即Y(n)=W(n)*X(n)。
    FIR滤波模块的输入Xin主要包括数据和权值系数两部分。采用字宽为12 bit的A/D转换器，将转换得到的数据存储在一个深度为N的静态随机存储器SRAM中，以此信号数据Din作为所设计的N阶FIR滤波器的输入量。开辟一个字宽为16 bit的ROM用以存储FIR的权值系数Coeffs，其中最高位表示符号位。乘加运算是靠复用12×16的乘法器和加法器来实现的。系统设计时，采用Verilog语言实现参数化乘法器，这样的设计有利于系统的简洁和稳定。SROM中的X(n)以及ROM中的系数W(n)的读取一定要遵从严格的时序，系统采用状态机输出地址信号来控制。乘加运算完成之后，会产生数据输出有效信号yvalid。A/D转换过程中会输出Next信号作为标志信号，表示数据转换成功，可以进行下一次运算。
　    参数化乘法器核心代码如下：
　　always@（posedge clk）
　　           begin
　           if(state<8)
　           begin
　　            addr<=addr+1′b1;     //时钟地址加1，乘法一次
　　            yvalid<=1′b0;
　           end
　　          else
　           begin
　　            state<=0;
　　            yn_out<=yout;
　　            yvalid<=1′b1;
　         end
　    end
　    always@(posedge clk)
　    begin
　        yout<=yout+re;    //累加
    end
2.4误差计算模块

　　误差计算模块是系统必不可少的一个部分,是对系统功能的强力补充,对于系统的完善有很大意义。FIR滤波器的输出和期望值会存在一定量的误差，利用该模块可实现此误差的计算。联系以下要介绍的权值存储模块中的数据和当前输入的数据进行信号的处理，该模块还会输出权值计算模块所需数据。根据上面FIR滤波器输出结果可知，当输出信号yvalid有效时，yn_out输出结果。yn_out输出结果作为可以计算误差的标志，在Next信号的上升沿时刻，根据有效的yvalid，通过一个减法器实现误差的计算。核心代码如下：
    always@（posedge next）
    begin
    if(yvalid)
    err<=dn-yn_out;
    end
2.5 权值计算及存储模块
    权值存储模块是关键的辅助模块，根据FIR滤波模块等各个处理模块的输出数据对信号的数据以及权值进行必要的更新。更新的数据还要存入存储模块。
３ 仿真及功能检验
    完成整个系统的功能测试需要进行大量的工作,以确保系统的有效性及工作的稳定性。软件的外围接口以及算法的功能性都需要经过反复调试。采用当下比较流行的FPGA设计软件Quartus II来进行测试与改进。
    Quartus II软件自带的仿真工具局限性很大，功能比较单一。如此复杂的一个系统的仿真分析对Quartus II软件本身来说是相当困难的，而Matlab是强大的数值分析及信号波形研究软件，因此利用Matlab和Quartus II软件的结合完成系统的仿真测试。利用Matlab产生复杂的仿真输入信号,再利用Quartus II进行仿真输出,并利用Matlab进行输出结果的分析和验证。2抽头的FIR自适应滤波器的LMS算法RTL结构如图6所示，其复杂度是FIR滤波器的3倍。
　仿真结果如图7所示，仅从波形上看，基本上实现了自适应滤波的功能，但是波形并没有达到很理想的状态，低阶的LMS模块自适应处理能力较弱，收敛性不好。这主要是因为在该设计中,FIR滤波器的阶数太小。因此，在实际制作FPGA时，自适应抽头数用10个。

    本文在深入研究自适应滤波器的理论和LMS算法的基础上，利用Xilinx公司最新生产的Spartan-6系列FPGA芯片,采用自顶而下的方法成功设计出一种基于FPGA的自适应滤波器。该设计结构清晰，原理明确，设置方便，并且调试起来十分简单。通过模拟仿真和时序检验，该横向自适应滤波器完成了设计的要求，可以达到明显的滤波效果，其性能满足很多领域中对滤波器的要求，实用性很强。
参考文献
[1] HAYKIN S S, WIDROW B. Least-mean-square adaptive filters[M]. John Wiley & Sons, 2003.
[2] 郭继昌，向晖,滕建辅，等.基于FPGA的FIR滤波器的实现[J].电子技术应用，2000，26(5):62-66.
[3] 杨跃忠，阙沛文，李亮．自适应LMS滤波器在FPGA中的实现[J]．微计算机信息，2006,22(11):158-160．