摘  要： 研究了一种基于差分法原理的MS跟踪算法。当MS跟踪目标位置发生较大偏移时，通过使用差分法提取的目标形心位置对其进行修正。实验结果表明，该方法应用于运动目标的跟踪具有良好的跟踪效果。
关键词： 帧差法；目标提取；目标跟踪；均值漂移

　近年来，目标跟踪是机器视觉领域比较活跃的研究课题，在车辆跟踪、智能机器人、人机交互、智能家居以及生物医学图像分析等行业有着潜在的应用[1-2]。学者们提出了大量的运动目标跟踪算法，在这些算法中，基于统计迭代思想的均值漂移MS（Mean Shift）算法，经常被应用于聚类、图像平滑、图像分割和跟踪等各种不同场合。该方法计算量不大，能够进行视频图像的目标跟踪[3]。
　目前，MS方法在计算机视觉领域的应用飞速发展。COMAIVICIU D成功地将MS方法应用到图像分割和目标跟踪中[4]。应用Lindeberg理论解决了MS方法在跟踪色块时特征空间尺度h的选取问题[5]。彭宁嵩等证明了在核函数窗宽固定的条件下，目标在其窗宽范围内进行缩放、平移运动并不影响Mean Shift跟踪算法空间定位的准确性[6]。贾静平等引入目标倾角的方法来跟踪旋转的目标[7]，但是该方法是采用试探的方法通过多次分别计算水平、垂直和旋转的自由度，然后分别取最优值。这种方法比较复杂，而且采用固定的变化大小，对目标变化的适应性不强。以上这些方法虽然在某些场合下跟踪效果比较满意，然而算法比较复杂、计算量大。
　基于MS的目标跟踪算法要求相邻两帧间目标位置必须有重合，因此，当目标的运动速度较小时，能够获得比较理想的跟踪结果。当目标运动速度较快且目标较小导致相邻两帧间的目标位置无重合时，该方法往往失效。差分法是常用的目标提取算法，可以快速有效地提取出目标的轮廓。利用差分法提取出目标的轮廓，进而计算出目标的形心位置，从而为MS跟踪算法提供准确、可靠的目标位置。本文主要研究动态复杂背景下图像序列中运动目标的跟踪技术。利用MS理论和差分法目标提取算法相结合，实现了运动目标的跟踪。通过对行驶中的小汽车的跟踪，验证了本文算法的有效性。
1 差分法目标分割及特征提取
　差分法也叫帧差法，是用当前帧图像减去前一帧图像，提取出运动目标，属于图像分割技术范畴，其原理比较简单，易于实现。
1.1 差分法原理
　基于像素灰度信息的差分算法速度快、提取准确，是运动目标提取首选算法。假定函数fk（x，y）、fk+1（x，y）分别表示第k帧、第k+1帧图像（x，y）处的像素值，则差分操作定义为：



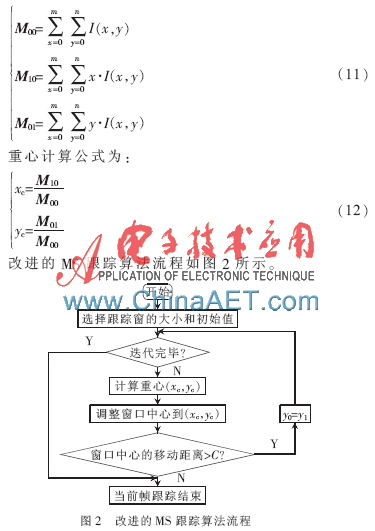
　一般来说，MS算法迭代若干次（一般在10次以内）后就可以逼近准确值。关于MS算法的收敛性，可参阅参考文献[10]。改进算法中的C为一个极小正数，通常取0.5，即半个像素。
3 实验结果与分析
3.1 跟踪算法仿真实验
　为了验证本文所提出的目标跟踪算法的性能，采用两组视频图像进行测试，并比较MS跟踪算法与本文跟踪算法的跟踪效果。所有算法均在Intel Pentium 4 3.0 GHz CPU、2 GB内存计算机，Windows XP系统下用MATLAB 7.9编程实现。图像中方框表示估计的目标位置，在图像序列中待跟踪目标的初始位置手动给定。
　图3是对一段长为70帧，帧速率为15 f/s的视频图像中沿着斜坡滚动下落小球的跟踪实验结果。其中,图3（a）是利用MS算法对第8、15、27、36、50和60帧图像中运动小球的跟踪结果，图3（b）是利用改进算法对相对应的帧图像中运动小球的跟踪结果。

3.2 跟踪算法评价
　跟踪方法的性能主要从精确度和实时性上进行评定。精确度主要是测试应用该算法在各种环境中能否比较准确地跟踪初始化的目标。为此需要计算跟踪偏差。
定义第i帧图像中目标位置的偏差ei为：
　ei=|Ti-Ci|　　　　　　　　　（13）
　其中，Ti表示在第i帧图像中跟踪目标中心的位置；Ci表示在第i帧图像中目标中心的准确位置，Ci的值可以通过人工的方式获得。
　定义目标跟踪的平均偏差为：

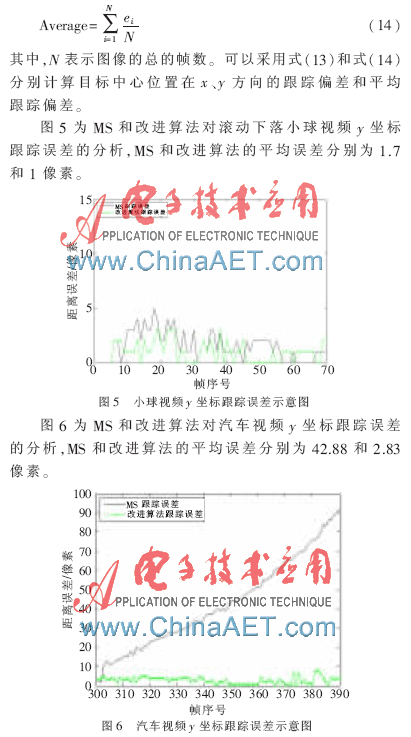
　本文提出了一种基于差分法的改进Mean Shift目标跟踪算法。通过差分法进行目标提取并计算目标的重心坐标，对Mean Shift算法进行自动修正。在目标丢失时，通过差分法修正跟踪位置，重新进行目标定位来获得稳定的跟踪。这种方法在跟踪偏移的情况下能够调整算法的目标模型分布，从而修正Mean Shift的跟踪过程。实验结果表明，本文所提出的方案实现了对运动目标的提取与跟踪。本文算法不足之处是没有考虑目标在运动时大小的变化，因此下一步的工作是研究跟踪窗口随着目标大小变化的自适应窗口跟踪。
参考文献
[1] 蔡荣太.非线性自适应滤波器在电视跟踪中的应用[D].北京：中国科学院，2008.
[2] 王亮，胡卫明，谭铁牛.人运动的视觉分析综述[J].计算机学报，2002，25（3）：225-237.
[3] COMANIEIU D， RAMESH V. Mean Shift and optimal Prediction for efficient object tracking[C]. Proceedings of the IEEE Conference on Image， 2000（3）：70-73.
[4] COMANICIU D， MEER P. Robust analysis of feature spaces： color image segmentation[M]. Los Alamitos， USA， 1997： 750-755.
[5] COLLINS， ROBERT T. Mean-shift blob tracking through scale space[D]. United States： Institute of Electrical and Electronics Engineers Computer Society， 2003.
[6] 彭宁嵩，杨杰，刘志，等.Mean Shift跟踪算法中核函数窗宽的自动选取[J].软件学报，2005：1542-1550.
[7] 贾静平，张艳宁，柴艳妹，等.目标多自由度Mean Shift序列图像跟踪算法[J].西北工业大学学报，2005，23（5）：618-622.
[8] FUKUNAGA K， HOSTETLER L D. The estimation of the gradient of a density function with applications in pattern recognition[J]. IEEE Transactions on Information Theory， 1975，21（1）：32-40.
[9] COMANICIU D， MEER P. Mean Shift： a robust approach toward feature space analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2002，24（5）：564-577.
[10] 李乡儒，吴福朝，胡占义.均值漂移算法的收敛性[J].软件学报，2005，16（3）：365-374.