基于迈克逊干涉原理的红外光谱仪可利用太阳光穿过待测大气的入射光进行光谱分析获得大气的物质成分信息，它主要由摆臂干涉仪、光电检测和光干涉图像数据采集处理几部分组成，如图1所示。

    基本工作原理为当单色光入射至反射率和透射率各为50%的分束器上时，会形成两束等强度的反射和透射光束。这两路光束各自通过反射镜(角镜、动镜)和固定的端镜重新返回到分束镜处，产生光干涉，两光束峰峰同相位时光强增加、反相位时抵消。当动镜运动时，引起光通过的光程变化，使最终形成的光干涉强度呈余弦变化，干涉强度为光程差的函数。对复合光的干涉图进行傅里叶逆变换即可获得反映物质成分的各单色光的光谱信息[1]。图1中，入射光1以45°角射入分束器，透射光2经角镜反射沿3-4-5-6-7-8-9返回分束器；反射光9经8-7-6-5-4-3-2返回，与透射返回光形成干涉后从10输出。与此同时，作为基准信号的激光也沿同光路形成干涉图样，利用激光探测器处理后可获得以光程差为周期的脉冲电信号，它的频率变化与干涉仪光程差速度变化对应，可将其作为实时的光程差速度反馈信号和摆臂转角位置反馈信号，同时还被用作太阳红外干涉图模数采样的触发信号，实现等光程差采样，以保证采集光谱的稳定性。在光程差已知的情况下，通过采集光源在某些点产生的干涉波形(光强弱变化规律)推断出哪种波长的光线被大气层吸收，就可以推断出大气层中化学物质的种类和含量。
    本文系统摆臂采用音圈电机[2]驱动，主要控制技术要求为：摆动角度±10°、光程差速度25.2 cm/s;调头时间75 ms；光程差速度稳定性为99%。
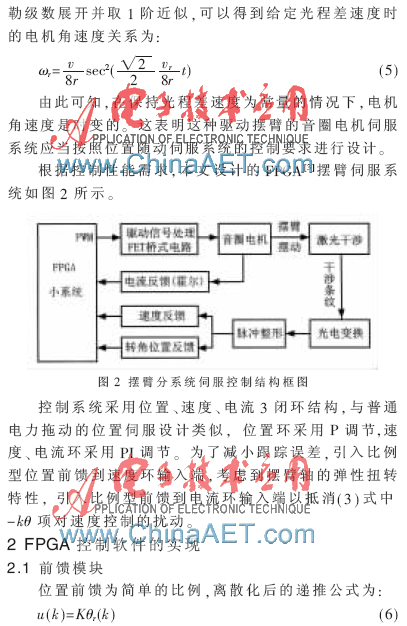
    摆臂伺服分系统在整个系统中的作用为：根据系统分析光谱分辨率的要求，控制摆臂机械部分在一定的角度循环摆动。摆动过程中，采集激光系统反馈的电信号，经过对电信号的信息处理，形成反馈信息，控制音圈电机带动摆臂转动，在规定范围内实现使光学系统光路以一定的速度匀速变化；同时实现相关分系统工作状态的监控功能，显示各系统的工作状态。
    由采样定律和光谱分辨率可知,要想获得优质的干涉图样，必需保证系统的采样间隔不大于1 ?滋m且采样点不少于30万个。在如此大量数据采集情况下，干涉图极易受诸多因素干扰，故其对摆臂分系统的运动速度控制精度、位移控制精度都有严苛的要求。另外，摆臂系统还受到空间的限制。摆臂必需在一定范围内完成循环摆动，若超出最大行程则极易损坏光学器件，使整个系统报废。在满足系统空间限制的情况下，摆臂系统还必需保证一定的采样时长，这就要求摆臂系统在有限空间内做往返运动时的调头要快速、稳定。


    在FPGA中，对位置指令作简单的乘法运算即可。系数Ｋ一般以浮点的形式出现，例如本文输入到速度环的前馈系数为Ｋ=１.35,运算时需考虑小数部分的取舍问题。本设计中采用的寄存器位数足够高，实现时将乘法模块中小数部分做移位化整进行运算，然后根据小数的位数舍掉相应的位数，再在高位补零。值得注意的是，由于对原指令做乘法运算，故一定要扩充存放前馈处理后指令数寄存器位数，否则会产生溢出危险。
    按照上面的功能要求和实现方法，运用Verilog HDL程序加以实现，其时序仿真如图３所示。其中data为模拟的位置指令，k为前馈比例系数，dataout为前馈模块输出。       

               
2.2 位置调节器模块
    位置调节器模块是将位置指令与位置反馈进行比较，取其差值，按预定算法运算后为系统提供位置调节输出，需要该模块含有偏差计算功能和比例运算功能。离散化后递推公式为：
　　u(k)=Kp[θr(k)-θ(k)]=Kpe(k)　　　　　　　　　　　  (7)
       采用FPGA实现时将反馈量与给定量转换为补码形式参与运算。根据二进制数的运算规则可知，两数的减法运算可方便地由加法电路来处理。为方便系统对反馈量的正负加以区分，设计中制定一位标志位用以区分反馈方向是否与指令给定方向一致，当反馈量相对于给定量为正时(电机运动方向与期望方向一致)，标志位置为0；当反馈量相对于给定量为负时(电机运动方向与期望方向相反），标志位置为1。标志位为0时表明位置偏差为反馈量减给定量，反馈量做取反加一运算后参与加法计算；标志位为1时表明位置偏差为给定量加反馈量，反馈量直接参与加法计算即可。在模块中设置两个寄存器分别存储给定值和反馈值的补码形式。对这两个寄存器值做加法运算后即得所需偏差值。为方便后续运算，设计中将偏差寄存器扩充一位作为符号标志位，当偏差值小于0时，将偏差寄存器最高位置1，反之置0。偏差值与Kp相乘即得位置调节器模块输出。
    该模块运用Verilog HDL程序加以实现,取Kp=150得到的时序仿真如图4所示。

      一般采用的增量式控制算法虽然可以减少运算量，加快FPGA处理速度，但其也存在一些缺陷。当系统在启动、停止或大幅度增减设定值时，短时间内系统存在的大偏差会造成PI调节器的积分积累,致使算得的控制量超过执行机构可能最大动作范围的极限控制量，最终引起系统超调，甚至引起系统振荡。本文采用积分分离算法来解决这一问题。实现方法是在积分累加器中设定一个限幅值，当积分累加器中的值超过此值时，调节器将积分功能屏蔽变为P调节器，并将累加器中的值清零，此时系统的输出只与当前时刻输入有关而与系统前期状态无关，这样可使系统状态突变(如换向运行)时快速响应，避免系统偏差累计引起振荡。当累加器中的值小于限幅值时，调节器为PI调节器。图5为带限幅值的PI速度调节器时序仿真图，其中设计取a=0.309，b=0.009，限幅值为512。
    从图5可见,模块在clk1上升沿动作，当偏差值preg没有超过给定限幅值时，addreg对偏差值做累和运算，data为模块比例环节输出，dout2为模块比例积分调节数。系统速度环使用PI调节器。而当偏差值大于限幅值时，addreg清零，此时积分运算环节关闭。当下一时钟上升沿来临时计算此时偏差值，若没超过限幅值积分环节重新参与运算。dout2最高位为符号位，0表示输出数为正数，1表示输出数为负数，如图中10045表示速度调节环调节指令数为－45。电流调节器设计完全相同，参数按典型1型系统设计[4]选取，不再重述。

3 实验结果与结论
    本文设计的图2所示控制系统采用16 V直流电源通过H桥对音圈电机供电，H桥所用场效应管型号为IRF510；电机为BEI公司的RA-10-002A；FPGA型号为EP2C8Q208C8N。利用FPGA构造位置、速度、电流调节器与相应反馈处理电路形成3闭环加前馈控制，输出PWM信号通过电平转换完成驱动,调制频率为40 kHz，电流采用霍尔取样[5]。

     实验获得的摆臂在±10°左右范围内周期摆动过程中对给定的25.2 cm/s光程差速度的跟踪特性如图6所示。由于速度采用PI调节，在快速调头的起动、制动到达指定速度时均存在一定超调，幸而系统在此加减速阶段的数据是视为无效的，本系统允许的调头无效数据时间为75 ms，实验结果的调头波形到达目标轨迹的时间小于66 ms，平均调头时间为65.1 ms。在整个稳定摆动区间，随摆角变化，音圈电机角速度的变化规律与式(4)描述的相一致，电机角速度绝对值最小为0.234 55 rad/s(摆臂摆动中心位置，对应电流过0位置附近)和0.237 15 rad/s(最大摆角处、调头前瞬间、如图中0.6 s附近位置)。音圈电机的电流如图6(a)所示，其中每伏对应电流0.8 A。由图可见，为了克服摆臂的弹性扭矩，电流随摆角线性增大，调头时，较大的反向电流促使摆臂迅速减速调头反向，完成调头后，线性增长的电流平衡弹性扭力，保证摆臂稳定运行。摆臂分系统的摆动运行周期约为2.5 s。实验采集获得的速度数据分析表明，在有效数据区域，虽然光程差速度的离散值在不停地变化，但其速度波动范围始终保持在0.7%范围，满足99%的性能指标要求。

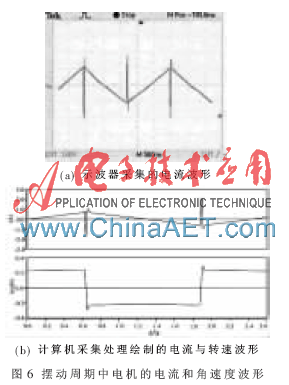
    实验结果表明，这种采用FPGA设计的伺服系统达到了预期的设计目标。对于调头过程中存在的超调，还可以进一步通过调节器控制策略的改进获得改善。
参考文献
[1] 窦秀明，代作晓，华建文,等. 音圈电机驱动光谱仪动镜的数字控制[J].科学技术与工程,2007，7(17)：4292-4295.
[2] 张大卫，冯晓梅.音圈电机的技术原理[J].中北大学学报(自然科学版),2006,27(3):224-228.
[3] 曾庆立，陈炳全.全数字直流电机PID控制器的FPGA实现[J].机电产品开发与创新，2008，21(1)：145-146.
[4] 杨耕,罗应立,等.电机与运动控制系统[M].北京：清华大学出版社, 2006:128-160.
[5] 王离九.电力拖动自动控制系统[M].武汉：华中理工大学出版社, 1991:95-112.