摘  要： 利用BP神经网络自适应学习，结合粒子群优化算法的全局搜索和遗传算法的快速收敛特性检测DDoS攻击行为。实验证明，新算法具有速度快、检测率高和误报率低的特点，能很好地应用于检测和抵御DDoS攻击。
关键词： DDoS；BP神经网络；粒子群算法；遗传算法

　DDoS是一种分布式大规模流量攻击方式，通过控制互联网上傀儡机对目标服务器发动攻击，产生的大量数据流涌向目标服务器，消耗服务器系统资源和带宽，或把链接占满，从而影响合法用户的访问。实施DDoS攻击一般都会伪造源IP地址，具有隐蔽性强、并发数高、攻击流量大、破坏力强、涉及范围广的特点。传统的DDoS检测方法很难界定突发流量与DDoS攻击流量。本文提出一种基于粒子群BP神经网络的流量检测模型，结合粒子群算法的全局搜索和遗传算法的快速收敛特性检测DDoS攻击行为，最后通过实验证明，新算法能够快速、准确地检测到各类DDoS攻击，具有很强的应用价值。
1 DDos攻击方式和检测方法
　DDoS攻击基于TCP 3次握手协议，按攻击方式分为直接型攻击和反射式攻击两类。直接型攻击是通过控制傀儡机向目标服务器发送大量数据流，耗尽服务器系统资源直至瘫痪。反射式攻击是伪造服务器IP向主机群发送虚假连接请求，致使主机群应答信息涌向服务器（如ＤＮＳ请求只有60 B，应答信息却有4 320 B，反射70多倍流量），通过占尽服务器接入带宽和连接上限阻止合法用户的访问。
　针对DDoS攻击通常采用的是基于特征库匹配检测、基于数据挖掘攻击检测和蜜罐技术[1]。特征库匹配检测需要搜集DDoS攻击数据包各种特征建立特征库，服务器对虚假连接请求特征进行匹配，若吻合则视为攻击。这种检测方法依赖于攻击特征的描述，对检测漏洞型DDoS很有效，但无法识别大量没有协议特征的攻击。基于数据挖掘攻击检测方法通过对数据包流量特征分析，将其中规律转换为检测规则，再根据网络流量特征是否偏离正常流量模型来判断攻击行为，其最大优点是能够检测没有协议特征的变种DDoS攻击，但是流量样本本身具有一定的随机性，使得算法复杂，计算量大，挖掘速率和准确性不高。蜜罐原本是一种网络诱骗技术，通过伪装真实系统特征吸引攻击者攻击蜜罐系统，而真正的服务器得以正常运行。蜜罐不能控制和阻断攻击行为，只有遭受攻击后才能检测到攻击，属于被动防御。上述3种方法都不能很好地解决复杂网络下DDoS欺骗攻击，相应的检测技术已明显滞后于攻击手段的更新。而抵御DDoS攻击的核心在于检测，因为只有检测到攻击行为防火墙才能实施包过滤，IDS才能追踪攻击源，服务器才能拆除虚假连接回收系统资源。如何检测DDoS攻击行为，提高算法匹配效率和准确率一直都是研究的难点和热点，也是目前亟待解决的问题。
　本文提出一种基于粒子群BP神经网络的流量检测模型，结合粒子群算法的全局搜索和遗传算法的快速收敛特性用于检测DDoS攻击行为。
2 BP神经网络自适应学习算法
　BP神经网络的自适应学习性由正向传播和反向传播构成。正向传播时数据从输入层流经各个隐含层处理后通过输出层输出结果。若期望值与输出结果偏差大于预设阈值，采用反向传播梯度法调整，重复两个过程直到偏差小于预设精度为止，从而学习和存储大量的输入输出映射关系，算法如下。
　（1）初始化神经网络向量。BP网络通过反复改变输入权值，使输出结果不断接近最优值。若输入层有n个神经元，隐含层有p个神经元，输出层有q个神经元，变量定义如下：

　（7）判断误差是否小于预设精度或最大迭代次数，满足条件则输出计算结果，否则返回到步骤（3），选取下一个学习样本进入下一轮学习。
　通过大量实例样本学习，BP神经网络的自适应学习特性不仅可以检测出流量中的DDoS攻击，还能识别未知攻击行为，从而克服传统依赖特征库匹配才能检测DDoS攻击的局限性。对DARPA 2000年数据分析表明，BP神经网络能准确检测间歇式DDoS流量攻击。为此，攻击者攻击手段也随之发生变化，从传统的恒速攻击和间歇式攻击转变为流量渐增式攻击和间歇式与速率渐增式组合攻击。此时，该方法需要学习流量中更多样本才能识别攻击行为，收敛速度慢，预设精度容易使算法陷入局部最优现象，影响检测率和误报率。
3 粒子群算法
　粒子群算法（PSO）是基于鸟类群体行为研究的模拟算法。鸟群在封闭空间随机搜索食物，并且在这个空间只有一个全局最优值。假如所有鸟都知道当前位置与搜索食物之间距离，那么找到全局最优解的最优方案就是从身边最近的鸟周围区域进行搜寻[2]。在粒子群算法中，寻找最优问题的每个解对应搜索空间的每只鸟，称为粒子。每个粒子的初始化向量代表鸟的飞行位置和速度，每个粒子通过寻找附近粒子迭代搜寻最优解，具体算法如下。

4 粒子群遗传算法在BP神经网络中的应用
　BP网络在检测DDoS攻击中需要事先建立网络正常流量参考标准，初始化权值和阈值参数难以确定，设置过小会使算法难以收敛，过大会陷入局部最优。在复杂网络中DDoS攻击具有间歇式和流量渐增式特点，攻击行为和流量特征往往不是简单的一对一等价关系，导致无法检测未知行为攻击。而PSO算法全局搜索能力强，但是收敛速度过慢，并且容易陷入局部最优解。因此本文提出基于BP网络自适应学习的粒子群遗传算法。
4.1 新算法实现思想
　新算法首先通过PSO搜索最优位置向量，将网络流量及其参数量化为每个粒子并初始化状态，从而构建神经网络粒子群，找出全局最优极值范围，以此作为BP网络的初始阈值，再引入遗传算法和变异算子加速向最优解的收敛速度和避免早熟现象。若得到的结果偏差超出PSO提供的预设阈值，再重复搜索过程，直到找出全局最优解。新算法融合PSO全局搜索能力、BP神经网络的学习过程和遗传算法的快速收敛优点，设计步骤如下。
　（1）确定BP网络隐含层数量，对每一网络流量进行粒子群编码，并进行粒子群初始化。
　（2）利用PSO算法找出全局最优极值范围，并判断是否满足结束条件（全局极值收敛速度大于偏导数δo或最大迭代次数）。如果满足结束条件则进入步骤（3）BP网络学习过程，否则根据式（7）和式（8）更新粒子的速度和位置，并重复本步骤。
　（3）将PSO找出的全局极值作为BP网络的初始阈值并进入学习过程，引入遗传变异算法向最优解加速收敛。
　（4）判断结果是否满足条件（群体适应度是否陷入局部最优和结果是否小于极值范围），如果都满足，则输出最优值；否则返回步骤（2）继续PSO算法的全局搜索。新算法流程图1所示。
4.2 早熟现象判定与处理
　PSO中的粒子当前位置和速度依靠个体极值和全局极值来引导，当粒子发现更优值时，其他粒子受到更优值吸引迅速聚拢，如果集聚点并非全局最优解，表示PSO陷入局部最优现象，加上遗传迭代，粒子之间的差异越来越小，导致早熟收敛。由于粒子个体适应度大小是由粒子个体位置和速率决定的，此时可以根据粒子整体适应度状态判断种群是否陷入局部最优。
　基于此思想，新算法根据适应度判断是否过早收敛，经过BP网络训练后，样本输出的误差总和均值为：

　遗传算法的变异算子将群体中优良个体通过交叉和变异操作遗传到下一代，维持种群的多样性，并且可以防止算法过早收敛的现象。
5 实验测试
5.1 流量样本特征采集和建模
　本文以KDD99CUP作为实验基础数据，通过对样本采集进行训练。本文选取1 000个模拟节点，用Sniffer抓包采集网络500组流量特征样本，其中包含正常的客户机连接请求和间歇式与速率渐增式DDoS攻击，典型采样结果如表1所示。

　从以上500组数据量化为PSO粒子群并初始化状态参数，选取典型200个粒子作为训练数据集，初始化种群微粒个数为20，测试函数维数分别为10、20、30，对应的最大迭代次数分别为500、1 000和100，设置初始惯性权重w=0.9，加速系数c1和c2为2.00。网络有4个输入节点和3个输出节点，确定BP网络结构，如图2所示。其中i、j、k分别代表输入层、隐含层和输出层的层数。因此网络中需要寻找24个高斯函数中心矢量，6个基宽向量和18个输出层连接权值，共48个参数，即算法中的粒子将在48维空间搜索满足最小均方误差要求的最优解。

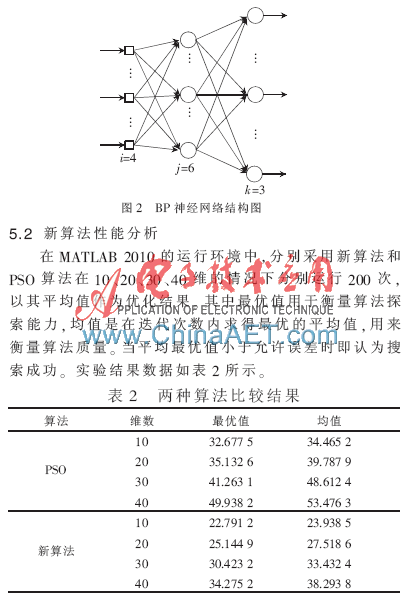
　从表2可以看出，在给定迭代次数下，新算法测试结果比PSO更接近最优值，计算精度有明显提高，充分体现了新算法的卓越性。
　在实验中，PSO算法参数初始化粒子数为200，加速因子c1=c2=2，最大迭代次数为2 000。新算法迭代次数和初始化粒子数等同于PSO算法，变异算子中的rand取值[0，1]，适应度Pm与迭代次数的测试结果如图3所示。

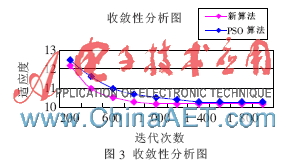
　从图3可以看出，新算法收敛速度快、误差小，性能明显优于PSO算法。当加速因子c1=c2=2时，新算法在迭代1 000次后无明显变化，找出全局最优解，而PSO算法要迭代到1 450次左右才趋于稳定，表明新算法通过变异算子向最优解加收敛，搜索的空间复杂度大为减少。
5.3 新算法检测率分析
　实验选取1 000个模拟节点对服务器发动SYN flood、LAND attack、TCP混乱数据包攻击、WEB Server多连接攻击、Web Server变种攻击和僵尸网络DDoS攻击共6种攻击方式，流量上采用渐增式和间歇式组合攻击，测试新算法对攻击行为的检测能力，结果如表3所示。

　从表3数据可以看出，对于带有明显特征的DDoS攻击行为（如SYN Flood和LAND Attack），3种算法检测率和误报率差别不大，新算法略有优势。然而对于未知行为和没有明显特征的DDoS攻击行为，如僵尸网络发动的DDoS变种攻击，僵尸主机通过伪造虚假IP地址发送大量SYN/ACK应答，使僵尸网络中攻击端发送的SYN请求与ACK应答数量达到平衡，攻击特征消失，此时基于特征匹配检测方法几乎失效，PSO检测率也不高，而新算法优势明显。
　新算法结合PSO全局搜索、BP神经网络自适应学习和遗传算法快速收敛的优点，检测DDoS攻击行为十分有效，可以检测未知攻击行为，可以将正常行为和攻击行为区别开来，具有较高的检测率和较低的误报率。
参考文献
[1] 李清华，张美凤．基于改进BP网络的染色合格率预测[J]．微计算机信息，2006（4）：93-95．
[2] 徐仙伟，叶小岭．遗传算法优化BP网络初始权重用于入侵检测[J]．计算机应用研究，2005（3）：38-42．
[3] 危胜军，胡昌振，姜飞．基于BP神经网络改进算法的入侵检测方法[J]．计算机工程，2005（13）：89-94．
[4] 仲兆满，李存华．基于神经网络的实时入侵检测系统的研究和实现[J]．计算机工程与应用，2007（30）：126-130．
[5] 易晓梅，陈波，蔡家楣．入侵检测的进化神经网络研究[J]．计算机工程，2009（2）：103-108．
[6] 潘昊，侯清兰．基于粒子群优化算法的BP网络学习研究[J]．计算机工程与应用，2006（16）：41-43．
[7] 曹承志，刘洋．基于改进粒子群算法的BP网络在DTC系统中的转速辨识[J]．系统仿真学报，2008（20）：77-81．
[8] 宋乃华，邢清华．一种新的基于粒群优化的BP网络学习算法[J]．计算机工程，2006（14）：181-183．
[9] Yu Zhenwe． An automatically tuning intrusion detection system[J]． Systems Man and Cybernetics，2007（2）：373-384．
[10] PARIKH D，CHEN T．Data fusion and cost minimization for intrusion detection[J]． Information Forensics and Security，2008（3）：381-389．
[11] BACE M． National institute of standards and technology[J]．NIST Special Publication on Intrusion Detection Systems，2000（7）：76- 79．
[12] LIPPMANN R， CUNNINGHAM R． Improving intrusion detection performance using keyword selection and neural networks[J]． Computer Networks，2000（4）：597-603．
[13] RICHARD LIPPMANN， ROBERT K CUNNINGHAM．Improving intrusion detection performance using key word selection and neural networks[J]． Computer Networks， 2000（9）：137-144．
[14] LI W， CANINI M， MOORE A． Efficient application identification and the temporal and spatial stability of classification schema[J]． Computer Networks， 2009（7）：252-261．
[15] LI W， CANINI M， MOORE A W． Efficient application identification and the temporal and spatial stability of classification schema [J]． Computer Networks， 2009（6）：790-809．
[16] CHE Z H． PSO-based back-propagation artificial neural network for product and mold cost estimation of plastic injection molding[J]． Computers and Industrial Engineering，2010（10）：236-242．
[17] KENNEDY J． Particle swarm optimization[J]． Neural Networks， 1995（10）：236-242．
[18] BAHEER A， HAJMEER M． Artificial neural networks fundamentals[J]． Computing Design and Application， 2000（10）：168-175．
[19] SUN J， FENG B． Particle swarm optimization with particleshaving quantum behavior[J]． Evolutionary Computation， 2004（5）：232-230．
[20] DORIGO M， BONABEAU E． Ant algorithms and stigmergy[J]. Future Generation Computer Systems， 2000（11）：269-275．