摘  要： 故障轴承的振动信号是非平稳信号，传统的非平稳信号分析手段存在许多不足；BP网络能够出色地解决传统识别模式难以解决的复杂问题。提出了经验模态分解（EMD）与BP神经网络相结合的滚动轴承故障诊断方法。采用EMD方法对振动信号进行分解，得到组成信号的多个内禀模态分量（IMF），提取重要的IMF分量的能量作为信号的特征量；采用BP网络作为模式分类器，对轴承的故障类型进行分类。经试验数据分析证明，该方法能够准确地对轴承故障进行诊断。
关键词： 经验模态分解（EMD）；BP网络；IMF能量；故障诊断

    滚动轴承的振动分为与轴承弹性有关的振动和与滚动表面状况有关的振动[1]。轴承故障的振动信号属于后者，其为非平稳信号。对于非平稳信号，时频分析是有效的分析手段[2]。加窗傅里叶变换可以对非平稳信号进行时频分析，但其只适用于缓变信号；双线性变换实际上不是线性变换，因此对多分量信号进行分析时会产生严重的交叉干扰分量；小波变换需要预先选取基函数，不具备自适应的信号分解特性。具有自适应性与正交性的经验模态分解方法（EMD），在分析非平稳信号方面具有强大的优势。
    本文采用经验模态分解方法(EMD)对轴承振动信号进行分解，获得组成信号的多个内禀模态(IMF)分量，并提取IMF分量的能量作为特征量；以BP神经网络作为模式识别器，对特征量进行识别和分类，从而实现轴承故障的诊断。
1 信号的EMD分解方法
    “筛分”是EMD分解方法的实质，“筛分”的目的是消除模态波形的叠加并使波形轮廓对称。为了有效找出信号的所有模态，EMD方法采用基于极值点的特征时间尺度参数[3]，把非平稳信号按特征时间尺度从小到大的顺序分解成多个内禀模态（IMF）分量。IMF分量反应了信号内部固有的波动特性，在它的每一个周期上仅包含一个波动特性，不存在多个波动模态混叠的现象[3]。一个IMF分量具有相同的极值点与过零点，且其上下包络线关于时间轴对称。复杂的非平稳信号能够通过EMD方法进行分解的基本假设是：任何复杂信号均可以由多个不同的且相互独立的IMF分量组成；一个复杂信号可以包含多个IMF分量，IMF分量相互叠加可以形成原复杂信号。

2 BP神经网络分类器
    对于轴承故障诊断，模式识别是其核心技术之一。BP网络具有自学习、分类和识别等诸多优势，能够出色地解决传统识别方法难以解决的复杂问题[5]。由于BP网络具有识别原因和故障分类的能力，所以BP网络是解决故障诊断模式识别问题的有效方法。
    BP网络具有良好的非线性映射能力、容错性和泛化能力，其结构简单，可塑性强，识别率高，抗干扰能力好，因此BP网络作为分类器广泛应用于故障诊断中。故障诊断的实质就是对不同的模式进行分类，本文将BP网络作为模式识别器对轴承故障进行分类。
   1989年，Robert Hecht-Nielsen证明了任何闭区间的一个连续函数都可以用单隐层的BP网络来逼近[6]。因此，具有单隐层和相应数量节点，且激励函数为Sigmoid型的BP网络可以完成任意n维到m维的映射。BP网络是一个“模式顺传播”与“误差逆传递”反复进行的过程，网络通过训练逐渐得到最优的权值，进而使网络的实际输出逼近期望的输出值。在BP网络的训练中，常采用批训练的方式，因为在样本数量较多时，批训练的收敛速度快[7]。批训练的过程如图1所示。

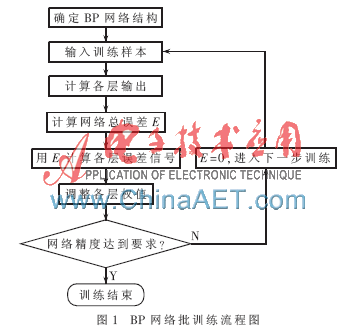
    在进行网络训练前首先应根据轴承工作过程的理论分析和实际运行经验，确定轴承出现故障的部位或原因，作为故障变量即网络的输出变量；同时确定用于区别各种故障的特征量作为网络的输入变量[6]。
3 提取特征量
    选择对工况状态最敏感的特征量是对工况进行有效识别的基础，并在很大程度上决定了状态识别的正确性[8]。不同故障类型的滚动轴承振动信号的IMF分量的能量具有明显区别，本文将选取其值作为信号的特征量。其步骤为：
    （1）采用EMD方法对采集到的振动信号进行分解，获取其各个IMF分量ci，其中i=1，…，n。图2为滚动轴承内圈有故障时的振动信号，图3为EMD分解图，图中给出了其前9个IMF分量。

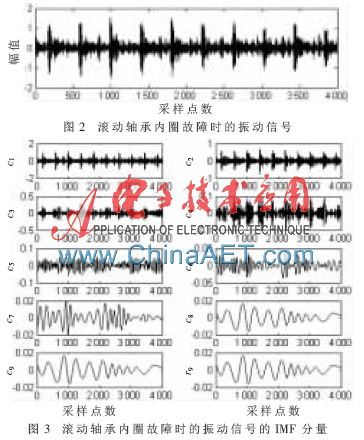
    （2）信号能量的定义如式（3）所示，但在实际的处理过程中，若信号为离散量，一般采用式（4）进行IMF能量的计算。

    采用EMD方法对原始振动信号进行分解，并从得到的分解信号中选取包含原信号主要特征信息的前8个IMF分量，按分解后的顺序依次命名为c1~c8。利用式（4）和式（5）构建振动信号的特征量P，把P作为BP神经网络的输入参数。将特征量P分成两部分：训练样本和诊断样本，分别对设计好的BP网络进行训练和诊断。部分训练样本如表1所示。

    模式分类器选取单隐层的BP神经网络。由前述可知，输入层节点的个数为8。实验中采集了4种轴承振动信号，采用“n中取1”表示法为输出层编码：正常轴承为[1，0，0，0]，内圈、外圈和滚动体故障的轴承为[0，1，0，0]、[0，0，1，0]和[0，0，0，1]，因此输出层的节点数为4个。根据输入层和输出层的节点数确定隐层的节点个数：m=（4+8）1/2+7≈10。将诊断样本输入训练好的BP网络，对不同类型的滚动轴承故障进行诊断和分类，部分诊断结果如表2所示。

    实验分析结果表明，EMD分解方法结合BP神经网络能够准确地对滚动轴承故障类型进行识别和分类。
    本文综合论述了EMD方法与BP神经网络相结合的滚动轴承故障诊断方法。该方法整体上包括4部分：信号采集、信号分解、特征量提取和模式分类。通过理论和实验分析可得出以下结论：
    （1）EMD方法能够将非平稳的振动信号分解成多个平稳的IMF分量信号；
    （2）IMF分量能量能够充分表征原始振动信号所包含的轴承故障信息；
    （3）EMD分解方法与BP神经网络相结合能够准确地对轴承故障类型进行模式识别和诊断。
参考文献
[1] 刘园，张永建，李元宝.改进小波能量分析法在轴承故障诊断中的应用[J].煤矿机械，2012，33(5)：254-255.
[2] 岳建海，裘正定.信号处理技术在滚动轴承故障诊断中的应用与发展[J].信号处理，2005，21(2)：185-190.
[3] 于德介，程军圣，杨宇.机械故障诊断的Hilbert-Huang变换方法[M].北京：科学出版社，2006.
[4] HUANG N E，SHEN Zheng，LONG S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proc.R.Soc.Lond. A，1998(454)：903-995.
[5] 钟秉林，黄仁.机械故障诊断学[M].北京：机械工业出版社，2002.
[6] 傅荟璇，赵红.MATLAB神经网络应用设计[M].北京：机械工业出版社，2010.
[7] 韩力群.人工神经网络教程[M].北京：北京邮电大学出版社，2006.
[8] 于婷婷.基于BP网络的滚动轴承故障诊断方法[D].大连：大连理工大学，2008.