文献标识码: A
文章编号: 0258-7998(2014)03-0123-03
随着电子商务的普及,人们网上购物的习惯逐渐形成。截止2012年11月30日,阿里巴巴集团旗下淘宝和天猫2012年总交易额已经突破一万亿。综合淘宝和天猫的交易数据来看,以快递员为主体的中国物流配送业对电子商务发展的促进起到了巨大作用。同时传统邮政担负的包裹配送业务比重也逐渐地倾斜于第三方物流配送公司。目前我国物流配送运输成本占整个物流成本的35%~50%左右[1]。由于网购物品用户分布在城市的不同地方,为了控制配送运输成本,改善配送秩序,需要优化配送路线。优化配送路线的求解有串行算法和并行算法。串行算法主要表现在基于算法本身以及其优化组合的方法,例如CLARK G和WRIGHT J的节约算法、GILLETT B E和MILLER L R的扫描算法、Christofides等人的k度中心树和相关算法、Gendrean的禁忌搜索方法、LAWRENCE J 的遗传算法、Dijkstra算法、Nordbeck提出的椭圆限制搜索区域改进算法[2]。随着计算数据的海量化以及摩尔定律的失效(晶体管电路已经接近了其物理改进的极限),串行算法本身的改进和组合已不能适应需求。计算机科学领域出现了另一类并行最短路径分析算法设计,目前关于并行最短路径分析算法设计有基于MPI的主从Dijkstra并行算法[3]、MPI+open-MP混合算法[4]、社区分析的最短路径LC-2q并行算法[5]等。
本文针对物流及时配送和成本控制需求,提出基于标色法的MapReduce广度优先算法并行化模型,并应用于配送线路优化问题。由于MapReduce本身封装了数据分割、负载均衡、容错处理等细节,用户只需要将实际应用问题分解成若干可并行操作的子问题,有效降低了求解难度,为解决物流配送运输路径优化问题提供了技术支持。
1 MapReduce算法描述
信息技术和网络技术的发展为云计算的产生提供了条件。MapReduce并行编程模型是云计算的核心技术之一。MapReduce是Google 实验室提出的一个分布式并行编程模型或框架, 主要用来处理和产生海量数据的并行编程模式,2004 年DEAN J和GHEMAWAT S第一次发表了这一新型分布式并行编程模型[6]。用户不必关注MapReduce 如何进行数据分割、负载均衡、容错处理等细节,只需要将实际应用问题分解成若干可并行操作的子问题,这种分解思路遵守主从架构模型。Mapreduce框架的主要程序分为Master、Map和Reduce。在Hadoop 中,MapReduce由一个主节点(Jobtracker,属于Master)和从节点(Tasktracker,属于Map和Reduce)组成[7]。
1.1 基于标色法的MapReduce广度优先算法模型
给定一个带权有向图,用G=(N,E,W)模型来表示,其中N={ni∣i=1,2,...,m}为完全图的点的集合;E={e(ni,nj)∣i≠j, ni,nj∈N}为弧段集;W={w(ni,nj)∣i≠j,ni,nj∈N}为权值集。一般向图的权值表示节点与节点之间的几何长度,记为w(ni,nj)=dij,dij表示节点ni到节点nj的距离。最短路径计算就是计算从起始点ni到终止点nj的最短几何长度之和为最小。在有向图起始点和终止点的最短路径计算中,MapReduce采用的是广度优先算法。MapReduce计算最短路径用邻接表来表示图,在邻接表中每一行数据构成Map和Reduce的一个数据内容。Map和Reduce的(key,value)中key为N,value值为与这个节点邻接的所有节点的 AdjacentList。在用标色法求解最短路径时,AdjacentList节点的信息包括源点到顶点的距离distance(除到本身的距离为0外,其余初始值皆为无穷大);节点的颜色color(其值可分别取0、1、2,0表示未处理的顶点,1表示等待处理的顶点,2表示已处理的顶点,源点的初始值为1,其余顶点皆为0);被访问顶点和边的权值记为N和W。顶点的数据结构如表1所示。

1.2 MapReduce求解步骤
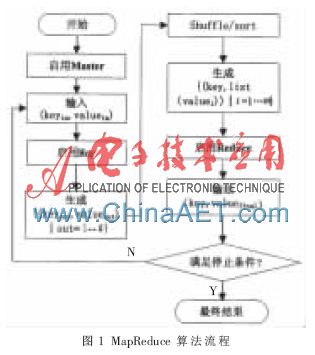
(1)Master对输入文件按行(每行代表图中的一个顶点)进行自动切分,并将数据作为输入分发到每个Map任务(keyin,valuein),即输入[(ID,<Distance;color;pnodes and weight>)];
(2)接收(keyin,valuein)对,当valuein中的color的值为1时,则处理当前顶点,产生临时的{(keyout,valueout)│out=1...k}集;
(3)MapReduce对Map执行过程输出的临时中间结果进行分组(Shuffle/sort),将相同的key值即ID号合并成同一组(key,list(valuei)│i=1...m),并将其分发给空闲的Reduce;
(4)Reduce接收(key,list(valuei)),对相同ID的value进行合并,找到当前的最短路径;
(5)如果每次Reduce后,结果收敛,则停止计算;如果未收敛,则继续发给下一轮的Map过程,多次迭代计算直到color值全部为2,得到最终的最短路径,算法结束。
MapReduce算法流程如图1所示。
1.3 MapReduce算法伪代码
(1)MapReduce的第一次迭代伪代码,Map部分为:
Map:<k1,v1> → list(<k2,v2>)
其中k1为节点的ID;v1为该节点的距离、边、边的权值、颜色;每一个输入的<k1,v1>会输出一批<k2,v2>,它们是计算的中间结果。
Begin
If( color(k1) = 1)
//如果k1的还需处理,即k1的颜色为灰色
{
for ki (<k1,ki>in k1.edges)
//对所有k1指向的节点, 只处理所有标记为1的节点
If ( distance(k1) + weight(k1 ,ki) < distance(ki))
{
Set distance(distance(ki)) = distance(k1) + weight(k1,ki);
Set color(ki) = 1;
emit (ki, v1)
//将该记录加入到键值对中,将标记为1
的节点所关联的节点加入中间结果。
}
Set color(k1) = 2;
//标记为1的节点被变更为2,表示处理完毕
}
emit (k1, v1)
End
(2)Mapreduce的第一次迭代伪代码,Reduce部分
Reduce <k2,list(v2)> → <k3,v3>
//<k2,list(v2)>输入的中间结果,其中list(v2)表示
一批属于同一个K2的value。<k3,v3>为输出结果
Begin
Set color(k2) =0;
Set distance(k2) = ∞;
vi∈ list(v2);
If( vi.color > k2.color)
//按照节点对计算中间结果进行合并
{
Set color(k2) = vi.color;
}
If {vi.distance < distance(k2))
//如果中间结果比原有结果小,将节点标记为1
{
Set distance(k2) = vi.distance;
If(vi.color = 1),Set color(k2) = 1;
}
If vi.edges != null, Set Edges(k2) = vi.edges;
}
emit (k2, vi.)
End
2 案例分析
2.1 基本情况
韵达快递浙江杭州西湖区文一路公司是民营韵达快运的子公司,为客户提供快递、物流及电子商务等一系列门到门服务。企业的配送范围为文一路、文二路、教工路及学院路构成的矩形区域,该区域面积大约20 km2的范围。
随着第三方物流公司的增多,物流配送竞争越来越激烈。为了压缩成本,按照配送点情况优化线路是节约成本的途径之一,优化后的单源配送线路线可以将途经的配送点一并发送,形成一车多配的节约模式。
2.2 问题提出及求解
公司某次接到为4个区域(西湖科技大厦、节能工业园、高新大厦及华门公寓)配送货物的任务,配送员决定分头配送,而如何组织好路线使得路程最短就可以归结为单源最短路径问题。为了计算方便,设置配送中心点为n1,被配送的4个地方分别设置西湖科技大厦为n2,节能工业园为n3,高新大厦为n4,华门公寓为n5。4个区域之间及其与配送中心的几何路线长度取整数(km)。有向图见图2(a),其中几何路线长度d1(n1,n2)=10,d2(n1,n4)=5,d3(n2,n3)=1,d4(n2,n4)= 2,d5(n3,n5)=4,d6(n4,n2)=3,d7(n4,n3)=9,d8(n5,n1)=7,d9(n5,n3)=6。从配送中心n1出发选取怎样的路线可以满足到达n2、n3、n4、n5的长度是最短的。采用标色法的MapReduce广度优先算法计算,依照伪代码的计算逻辑计算出源点到其他各点的最短路径。通过4次迭代顶点到各点的最短路径见图2(f),其中加粗的圆圈表示被访问过的顶点,color值为2,圈内的数值为其与n1的最短路径长度;color值为0,虚线圈为未访问的顶点,圈内值为∞;color值为1,虚线圈为待访问的顶点,圈内值为标注值。MapReduce第一次迭代验算数据如表2所示,其余几次迭代过程格式与此类似。
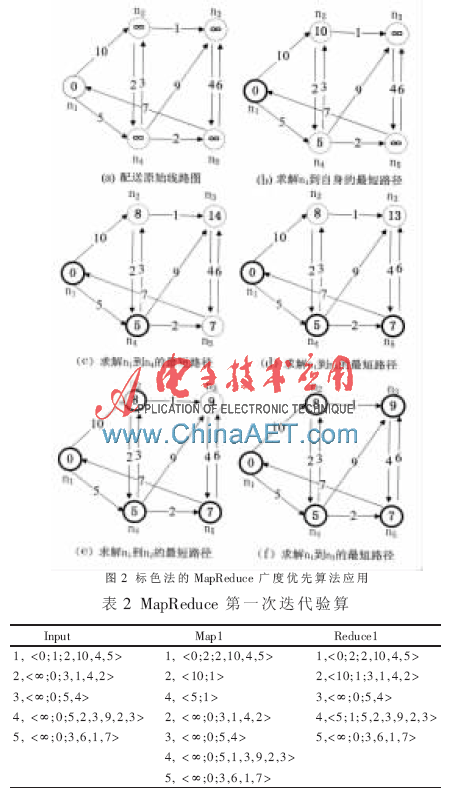
如果从配送点n1到节能工业园n3进行配送,配送的最优路线就是配送点n1→高新大厦n4→西湖科技大厦n2→节能工业园n3。优化后的长度为n1→n4→n2→n3=9。相比其他配送路线选择,如
n1→n2→n3=11,n1→n2→n4→n3=21,n1→n2→n4→n5→n3=20,n1→n2→n4→n5→n3=20,n1→n4→n3=14,n1→n4→n5→n3=13,优化后的路线长度更短。在选择这样的配送路线后,途中高新大厦n4和西湖科技大厦n2的一些货物也可以一并被配送,这样就满足了一车多配的情况,达到了节约成本的目的。
本文将MapReduce并行编程模式引入了物流配送最短路径查询,用户不必关注MapReduce 如何进行数据分割、负载均衡、容错处理等细节,只需将实际应用问题分解成若干可并行操作的子问题,即可解决配送线路优化问题,简化了算法设计。为优化配送、节约成本、提高配送系统的运行效率提供了技术参考。
参考文献
[1] 刘荣华,孙皓,赵娟.基于供应链的运输决策研究[J].中国海洋大学学报,2007(1):63-65.
[2] ZHAN F B. Three fastest shortest path algorithms on real road networks[J]. Journal of Geographic Information and Decision Analysis, 1997,1(1):69-82.
[3] 卢照.基于城市路网最短路径并行搜索算法的研究[D].陕西:陕西师范大学,2010.
[4] 杨庆芳,刘东,杨兆生.基于MPI+openMP混合编程模型的城市路网最短路径并行算法[J].吉林大学学报(工学版),2011,41(6):1581-1584.
[5] 马明全,周明全,耿国华,等.基于社区分析的最短路径计算[J].计算机应用与软件,2009,25(4):177-181.
[6] DEAN J, GHEMAWAT S. MapReduce:simplified data processing on large clusters[J]. Communications of the ACM,2005,51(1):107-113.
[7] 刘晓群,邹 欣,范 虹.基于并行云计算模式的建筑结构设计[J].电子技术应用,2011,37(10):123-125.

