摘 要: 针对传统的凸集投影(POCS)算法重建后的结果图像存在边缘模糊的问题,提出了一种通过小波变换与分形插值得到高分辨率初始图像的估计方法。该方法通过对一幅图像进行小波分解得到低频重构图像和高频重构图像,对高频重构图像使用分形插值保留了图像的纹理和边缘信息。仿真实验结果表明,该方法可行有效,改善了图像的边缘特性及整体质量,与传统的POCS算法相比,本文方法提高了重建图像的峰值信噪比。
关键词: 超分辨率; 凸集投影; 小波变换; 分形插值
凸集投影(POCS)超分辨率重建中,对高分辨率初始图像的预估直接影响该算法是否可行,并决定重构图像的质量。超分辨率重建技术可以在不改变成像条件的前提下克服图像系统原有的分辨率限制,提高图像的输出尺寸和质量,在视频监控、物联网、视频娱乐、卫星通信和远程医疗等领域都具有重要的应用价值[1]。
POCS超分辨率重建算法能够有效地结合先验信息,具有高度的灵活性和良好的可扩展性。国内外很多学者对该算法进行了大量的研究,1982年,Loyal和Webb最先将POCS理论应用于影像复原;Stark和Oskoui首次提出了最早的基于POCS的超分辨率重建算法,该算法简单且运算速度快,但没有考虑噪声的影响,得到的图像质量较差;Toecap和Sezan在此基础上提出了包含系统矩阵的运动模型,将点扩散函数引入POCS算法中,该算法可以模拟图像在传输过程中产生的模糊[2];参考文献[3]提出了通过双3次插值法获取高分辨率初始估计图像,相对于传统方法,该方法改善了图像的峰值信噪比。
本文针对传统的POCS算法存在的边缘模糊现象,通过小波变换与分形插值相结合的方法获取高分辨率图像的初始估计图像。该方法可以有效地改善图像的重建效果,与传统的POCS算法相比,提高了图像的峰值信噪比,改善了图像边缘质量。

通过对这些限制集合进行求交,形成超分辨率重建问题的解空间,超分辨率重构图像的可能解空间一定位于所有这些约束集的交集中。凸集投影过程指的是从给定向量空间中的任何点开始不断搜索,直到找到满足所有凸约束集的解的过程[4-6]。POCS超分辨率重建算法实现的基本流程是,首先通过超分辨率图像降质模型得到低分辨率图像序列,选定其中一帧图像作为参考帧,对参考帧图像插值建立高分辨率图像的初始估计图像,然后对低分辨率图像序列进行运动估计,最后基于PSF模糊函数对初始估计图像进行修正,直到得到可以接受的结果[7-8]。
2 改进的POCS算法
传统的POCS算法通过对低分辨率图像序列中的一帧图像进行双线性插值得到高分辨率图像的初始值[6],而传统的插值方法具有低通滤波器的性质,会使高频信息受损,使图像的边缘变得模糊。针对这一缺点,对高分辨率初始图像的获取方法作出改进,将小波变换与分形插值结合,有效地保留了图像的纹理及边缘等高频信息。本文改进的方法框图如图1所示。



通过改进的方法得到初始估计图像后,采用块匹配的运动估计方法估计出低分辨率图像序列信息在待恢复的高分辨率图像中的对应位置,确定由低分辨率图像的子像素运动所形成的位移算子[9]。使用运动估计的结果对低分辨率图像和初始估计图像进行运动补偿,然后基于PSF点扩散函数对初始估计图像进行修正,不断迭代图像残差项,直到得到满意的结果。为了改善重构图像的齿轮现象,在迭代过程中加入一次巴特沃斯滤波进行少许平滑。本文的POCS算法框图如图2所示。

3 仿真结果及分析
为测试本文方法的性能,在MATLAB R2012b仿真平台上分别对lena(256×256)、 typewrtr(256×256)、Car_1(512×512)、Car_2(512×512)和Car_3(512×512)等多幅JPEG图像进行仿真,将本文所提方法与传统的POCS算法进行比较。
通过lena图像介绍仿真的具体过程。对lena图像进行仿真时,采用的低分辨率图像序列由原始高分辨率256×256的图像经过图像降质模型获取,降质过程主要包括模糊、全局平移、下采样和噪声等操作。低分辨率图像帧数选为4帧,运动模型选择仿射运动模型,点扩散函数选用标准差为1 ,支撑域为5×5的高斯函数,各帧低分辨率图像的大小均为128×128,重建后的图像大小为256×256。
如图3所示,图3(b)中的4幅低分辨率图像序列是由图3(a)中的原始高分辨率图像经过降质模型生成的,选择低分辨率图像序列中的第一帧作为重构高分辨率图像的参考帧,即由该图来得到高分辨率图像的初始估计。为了比较结果,仿真实验分为两种情况进行:第1种情况,选用双线性插值,分辨率提高2倍,迭代次数选为10,得到的初始估计细节部分图像如图4(a)所示,高分辨率图像如图5(a)所示;第2种情况,使用本文提出的方法,分辨率提高2倍,迭代次数为10,得到的初始估计细节部分图像结果如图4(b)所示,高分辨率图像如图5(b)所示。


对比图4(a)和图4(b)可以看出,在对参考帧图像进行双线性插值放大之后,眼睛和帽檐的细节变得模糊,边缘的齿轮状明显,而在图4(b)中,明显看出这些部分可以较清晰地重建,边缘质量得到很好的改善。对比图5(a)和图5(b)也可看出,本文算法得到的图像清晰度优于传统的算法。
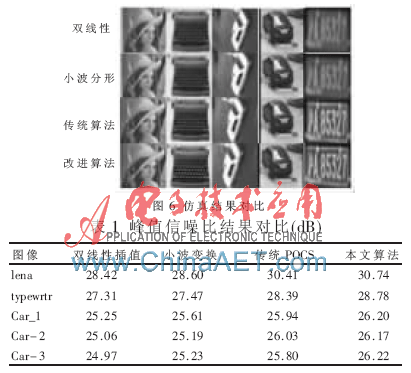
从图6的仿真结果可以看出,本文的方法得到了很好的主观视觉效果,改进后的重构图像整体质量得到了改善。本文采用峰值信噪比的客观评价标准来评价算法,表1给出了峰值信噪比结果,改进后的方法较传统的POCS算法峰值信噪比平均提高了0.308 dB,其中Car-2图像虽然仅提高了0.14 dB,但是其重构后图像的视觉效果得到显著提高。
本文通过对高分辨率初始图像的估计方法进行改进,通过改善初始值的细节及边缘质量,使得最终重构图像的质量得到提高。通过MATLAB对该算法进行了仿真,结果表明,该算法与传统的POCS算法相比,提高了峰值信噪比,改善了图像的边缘模糊现象,得到了良好的视觉效果。该方法对超分辨率重建技术在其他领域的应用也具有一定的意义。
参考文献
[1] PARK S C, PARK M K,KANG M G. Super-resolution image reconstruction: a technical overview[J]. IEEE Signal Processing Magazine, 2003,20(3):21-36.
[2] 陈光盛, 李树涛. 空域超分辨率图像融合算法研究[D].长沙:湖南大学,2006.
[3] 禹晶, 苏开纳.一种改善超分辨率重建中边缘质量的方法[J].自动化学报,2007,33(6):577-582.
[4] 李慧芳,杜明辉.基于改进的POCS算法的超分辨率图像恢复[J].华南理工大学学报(自然科学版),2003,31(10):24-27.
[5] OGAWA T,HASEYAMA M. Semantic image retrieval based on POCS algorithm using kernel PCA and its performance verification[C].IEEE 13th International Symposium on Consumer Electronics, 2009:582-583.
[6] Zhang Fan, Zhu Qidan. Super-resolution image reconstruction for omni-vision based on POCS[C]. Proceedings of Control and Decision Conference, 2009:5045-5049.
[7] 黄华,孔玲莉,齐春.基于凸集投影和线性过程模型的超分辨率图像重建[J].西安交通大学学报,2003,10(37):1059-1062.
[8] PROTTER M, ELAD M. Super resolution with probabilistic motion estimation[J]. IEEE Transactions on Image Processing,2009,18(8):1899-1944.
[9] TONG C S, LEUNG K T. Super-resolution reconstruction based on linear interpolation of wavelet coefficients[J].Multidimensional Systems and Signal Processing,2007,18(2-3):153-171.
[10] 浦剑,张军平,黄华.超分辨率算法研究综述[J].山东大学学报,2009,39(1):27-32.

