文献标识码: A
文章编号: 0258-7998(2014)06-0119-04
近几年来,随着MA Y[1-2]等人提出了基于稀疏表示分类的人脸识别,掀起SRC在人脸识别领域应用的热潮。郝静静[3]等人提出一种改进的人脸识别方法,效果得到明显提高。SALAH R[4]等人结合纹理特征提取和稀疏表示实现人脸表情的识别。Zhang Shiqing[5]等人把Gabor小波和局部二值化(LBP)分别用于表情特征提取,评估稀疏表示分类(SRC)的性能,并与支持向量机(SVM)、NSC、NNC等进行了比较。MAHOOR H[6]等人对人脸运动单元进行稀疏表示实现表情识别,并与SVM、NSC方法进行了比较。但表情特征相对于人脸特征复杂,表情样本少,加大了表情识别难度;直接运用SRC实现表情识别效果不是很好。邹修国[7]等人把人脸识别系统应用到DSP,为识别系统广泛应用奠定了基础。
针对上述识别方法的优缺点,本文提出双模板稀疏表示算法对人脸表情进行识别。通过增加正、负模板重构新的观测矩阵,优化了稀疏表示的性能,减少噪声、遮挡等对表情识别的影响,提高了表情的识别率。
1 基于稀疏表示的表情识别
1.1 稀疏表示理论
稀疏表示SR(sparse representation)可称为压缩感知,在很多领域扮演了越来越重要的角色。在式(1)中,稀疏表示理论的核心是在过完备矩阵D∈Rm×n下,重构出的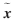 逼近原信号x,可理解为求解方程的过程:
逼近原信号x,可理解为求解方程的过程:

在实际应用中,当m<<n时,式(1)有无穷多解,即该方程是欠定方程。通过下式得到的最稀疏解x0即最小l0范数解:
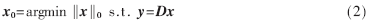
但式(2)的求解过程是一个NP-hard问题,计算效率极低。参考文献[8]指出,在满足约束等距性RIP的条件下,最小l1范数解逼近最小l0范数解。所以,可以在解集合寻找最小范数解(min‖x‖1)来代替求min‖x‖0,这是一个凸优化问题,用式(3)表示:
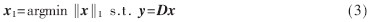
对于上述最优化问题,有许多l1算法[9]能够有效地求解,包括正交匹配追踪算法、LASSO、SPGL1算法等。
1.2 基于稀疏表示的表情识别算法
从表情库中随机取大部分人脸图像作为训练样本,用于构建测试样本对应的冗余字典。设第i类训练样本用矩阵表示为 ,每个图像用v来表示。将k类共n个训练样本组合在一起形成整个训练集矩阵D:
,每个图像用v来表示。将k类共n个训练样本组合在一起形成整个训练集矩阵D:
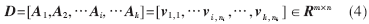
其中,m表示样本的像素点,ni表示第i类样本数目。通过求解出测试人脸在由训练样本构成的字典里的表示,可以知道测试人脸的表情类别信息。给出一个属于第i类的测试样本y,可以表示为:
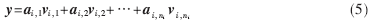
测试样本仅用来表示自同一类训练样本的线性组合,其他类别的系数为零,即求解出的解x1=[0,0,…,0,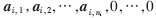 ],只有第i类的值是非0元素。系数向量a中包含大量有利于分类的信息。判断测试样本所属类别的公式为:
],只有第i类的值是非0元素。系数向量a中包含大量有利于分类的信息。判断测试样本所属类别的公式为:

其中δi(x1)∈Rn,是第i组系数中非零的数为系数x1中与i对应的那些数。ri(y)=‖y-Aδi(x1)‖2表示的是y与Aδi(x1)的残差值,认为残差值最小的对应类别i为y的类别。
2 双模板稀疏分类算法
实际应用中,训练样本个数和单样本的像素点影响原信号重构的效果。直接用训练样本来构造冗余字典D,重构效率很低。由于图像中含有噪声干扰,为了解决噪声的影响,式(1)改写为:

其中,ε表示误差向量,它与稀疏解x一样含有大量的稀疏零点。因此,为了方便计算,把解x和ε合并起来,添加一个模板I去构造新的矩阵B,故y可以表示为:

其中,B=[D,I]∈Rm×(n+m)。由于m<(m+n),所以方程(8)一直是欠定方程,ω的解并不唯一。把矩阵I用单位矩阵表示,I的向量ii∈Rm中只含一个非零数,用来表示图像中零散的噪声点。单模板I通过向量e帮助x分担原图像的零散噪声,使更多有用信息集中于向量x上。
原则上,观测矩阵D在没有限制的条件下,系数x可以为任何实数。然而,在识别的应用中,被识别的目标应该被训练样本用非负系数所表示。在训练样本库中,寻找到类似测试样本类别的个体时,主要集中于该类似样本的非负系数上。然而,直接对上述的辅助稀疏x、e进行非负约束不太合理。因此,本文在正模板的基础上提出了双模板的扩展矩阵。如图1所示,由训练样本矩阵、正模板和负模板共同构造双模板的观测矩阵。把测试样本中可能存在的负值转移到负模板,消除负系数对稀疏解x用于分类时的影响。此时,式(1)可写为:


图1 双模板观测矩阵
其中,e+∈Rm,e-∈Rm分别为正辅助系数和负辅助系数向量,新观测矩阵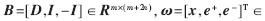 Rn+2m是非负系数向量。此时,负模板-I中的每一列向量-ii只含有一个零值,与正模板的ii刚好相反,可以减少稀疏表示中对n的要求,解决样本数不够的问题。式(8)的矩阵B中m<2m+n,因此是欠定方程,且ω没有唯一的解。通过变换域把式(8)求解问题转化为l1-正则化最小平方问题,稀疏表达式表示为:
Rn+2m是非负系数向量。此时,负模板-I中的每一列向量-ii只含有一个零值,与正模板的ii刚好相反,可以减少稀疏表示中对n的要求,解决样本数不够的问题。式(8)的矩阵B中m<2m+n,因此是欠定方程,且ω没有唯一的解。通过变换域把式(8)求解问题转化为l1-正则化最小平方问题,稀疏表达式表示为:

其中‖·‖1和‖·‖2分别表示l1和l2范数。本文使用l1范数解法l1_ls求稀疏解x。然后把稀疏解x代入式(6),求出残差值,即可得到测试样本y对应的类别。
对于一个有效的测试人脸,所求的非零系数集中于单个训练目标。为了衡量观测矩阵的性能,参考文献[4]定义稀疏集中指数(SCI)来测量稀疏系数集中程度:
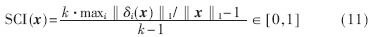
如果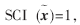 则测试样本只用一个目标样本来表示;如果
则测试样本只用一个目标样本来表示;如果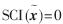 ,则测试样本的稀疏表示均匀地分布在所有样本中。
,则测试样本的稀疏表示均匀地分布在所有样本中。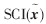 的值越大,说明求解的x稀疏性越好。本文将通过衡量SCI指数比较DT-SRC和SRC的性能。
的值越大,说明求解的x稀疏性越好。本文将通过衡量SCI指数比较DT-SRC和SRC的性能。
3 实验及结果分析
3.1 JAFFE人脸数据库上的实验
对人脸库的图像进行几何归一化、灰度归一化、滤波等预处理。JAFFE人脸图像经过预处理后大小为64×64,如图2所示,从左到右依次为愤怒、厌恶、恐惧、开心、自然、伤心、惊奇7种表情。

图2 KA的7种表情预处理后的图像
把JAFFE人脸库的210张图片按7种表情进行分类,每人每种表情随机抽取一个作为测试样本,其他为训练样本。对人脸图像进行下采样降维,针对SRC和DT-SRC算法选择最优的下采样率,采样点为15×7,比较NSC、SRC和DT-SRC的识别性能。
表1中平均SCI指数为统计70个测试人脸的每个SCI指数后求平均值,它能反映出稀疏表示分类的识别性能。从表1可以看出,DT-SRC相对SRC和NSC在识别率上有很大的提升,但牺牲了一定的时间;SRC和NSC的识别率差不多。

图3中,SCI指数的范围为[0,1],指数越接近1,所求得的解越稀疏,稀疏性越好。从图3可以看出,在第12、50个测试样本时SCI都很低,可以认为这些样本类别不能很好地被识别,所含的表情分类信息不明显;DT-SRC的SCI指数普遍比SRC的高,则DT-SRC的重构效果比SRC有了很大的提高。
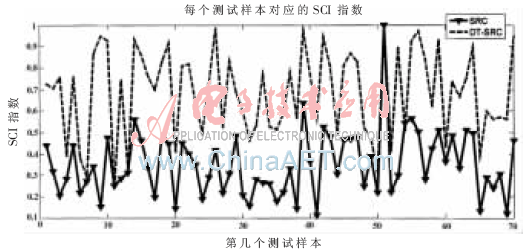
图3 JAFFE的测试人脸在SRC、DT-SRC的SCI指数
本文取图3的第70个测试人脸图,列出该图在DT-SRC和SRC下的残差值,如图4所示。图4(a)为第70个人脸的裁剪图,图4(b)和图4(c)中的横坐标1~7分别表示愤怒、厌恶、恐惧、开心、自然、伤心、惊奇的7种表情。图4(b)、图4(c)的第7个方柱(惊奇)的残差值最低,可以判断出图4(a)的类别是惊奇,该人脸的表情是惊奇。从图4可以看出,DT-SRC的第7类表情残差值相对其他类表情要明显,所求解的系数x在表情类别中主要集中于惊奇处。图4(b)中最低两个残差值的比例大约为1 400/100=14:1;图4(c)中最低两个残差值的比例大约为500/200=5:2;在该测试人脸的识别中,DT-SRC算法比SRC有更好的稀疏性和分类效果。

图4 某个测试人脸的残差值图
3.2 在CK人脸数据库上的实验
3.1节实验同样适用于Cohn-Kanade(CK)表情库。选取裁剪成64×64的CK人脸库作为实验数据库,把其中一人的7种表情显示如图5所示,从左到右依次为厌恶、恐惧、开心、自然、伤心、惊奇、愤怒7种表情。

图5 CK的7种表情预处理后的图像
CK库有18个人,每个人每种表情有5张,有7种表情,共有630张图像。每人每种表情随机抽取一个作为测试样本,其他为训练样本,则总有126张测试样本、504张训练样本。然后比较NSC、SRC、ISRC 3种算法的识别率,实验结果如表2所示。计算每张CK测试人脸在SRC、DT-SRC识别后的SCI指数,126张测试人脸的SCI指数如图6所示。

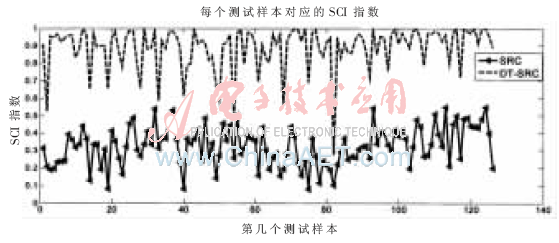
图6 CK的测试人脸在SRC、DT-SRC的SCI指数
分析表1和表2可知,SRC和NSC在识别时间上比其他方法有绝对的优势,而且识别率也较好。在CK库中的识别率明显比JAFFE库好,这是因为所使用的CK库的图片质量好,各表情差异明显。DT-SRC比SRC和NSC在识别率方面有所提高,特别是在图片表情特征不明显的情况下,识别率能有很大的提高。其实,在CK库中所使用训练样本比较多,SRC算法能达到很高的识别率。但在JAFFE库里,由于表情库的样本不多,导致字典D的列数不够,不能充分发挥出稀疏表示的作用,从而导致它的识别率低。而本文的算法DT-SRC弥补了字典矩阵D列数不足的缺点,且降低了噪声和负系数的影响,使识别率得到提高,但牺牲了一定的运算时间。
从图3和图6的SCI指数图看出,DT-SRC的SCI总体上比SRC的高,DT-SRC的稀疏表示性比SRC的好。当测试样本不是有效的人脸时,DT-SRC能更好地排除该张图片,减少错误的判断。
本文提出的DT-SRC实用性强、效率高,降低了识别的复杂度,解决了SRC用于表情识别时效率不高的问题。通过SRC与DT-SRC的比较,发现字典矩阵D的构造影响着正确识别率和稀疏分类性能,D中的元素能最大程度地表示测试样本的结构,且所添加的正、负模板可消除噪声、负系数等影响。因此,DT-SRC在表情识别方面效果不错。
参考文献
[1] WRIGHT J, YANG A Y, MA Y,et al. Robust face recognition via sparse representation[J]. Pattern Analysis and Machine Intelligence, 2009,31(2):210-217.
[2] JIA K,CHAN T H,MA Y. Robust and practical face recognition via structured sparsity[C]. European Conference on Computer Vision(ECCV), 2012:331-344.
[3] 郝静静,李莉.一种基于KPCA与LDA的人脸识别改进算法[J].电子技术应用,2013,39(12):132-134.
[4] SALAH R, KHOLY A E, YOUSSRI M. Robust facial expression recognition via sparse repre-
sentation and multiple gabor filters[J].International Journal of Advanced Computer Sciences and Applications, 2013,4(3):82-87.
[5] Zhang Shiqing, Zhao Xiaoming, Lei Bicheng. Robust facial expression recognition via compressive sensing[J].Sensors, 2012,12(12):3747-3761.
[6] MAHOOR H, ZHOU M, KEVIN L,et al. Facial action unit recognition with sparse representation[C].Automatic Face & Gesture Recognition and Workshops(FG2011), 2011:336-342.
[7] 邹修国, 李林, 陆静霞. 基于DSP的人脸HU矩识别研究[J].电子技术应用,2013,38(11):150-153.
[8] CAND?魬S E J, WAKIN M B. An introduction to compressive sampling[J]. Signal Processing Magazine,2008,25(2):21-30.
[9] YANG A, GANESH A, MA Y,et al. Fast L1-minimization algorithms for robust face recognition[J]. IEEE Transactions on Image Processing(TIP), 2013,22(8):3234-3246.

