文献标识码: A
文章编号: 0258-7998(2014)06-0033-03
当前在信息与通信领域,无论是为了解决能源问题还是满足产品本身的需要,如何设计低功耗通信电子产品已成为当前国际上的研究热点之一。数字滤波器是各类电子系统中重要的组成部分,从实现的网络结构上可分为有限冲激响应(FIR)滤波器和无限冲激响应(IIR)滤波器。对同样的设计要求,FIR滤波器通常比IIR滤波器需要更高的阶数,但FIR滤波器较IIR滤波器更为优化和简单,且能保证绝对稳定和线性相位,因此在语音图像处理、数字电视系统等领域都得到了极广泛的应用[1-2]。数字滤波器实质上是一系列包括加法、乘法和数据传输在内的运算,最终要用物理器件来实现。当把这些设计好的数字滤波器用现场可编程门阵列(FPGA)器件来实现时[3],通常用综合后的逻辑单元LE(Logic Element)数来衡量硬件消耗。子项空间技术利用滤波器系数之间的子项共享,可以有效减少滤波器实现时加法器的个数[4-8],从而降低实现复杂度,节省硬件资源。
1 子项空间及子项共享
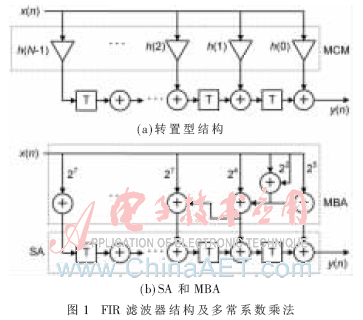
图1(a)为FIR滤波器的转置型结构。在这种结构中,输入信号与滤波器的各个常系数h(k)(k=0,1,…,N-1)相乘并送入延时单元,这种操作通常被称为多常数乘法MCM(Multiple Constants Multiplication)问题[9],可以用移位寄存器和加法器网络来实现。因此,加法器可以进一步分为延迟单元的结构加法器SA(Structural Adders)和常数乘法单元的加法器MBA(Multiplier Block Adders),如图1(b)所示。当滤波器阶数固定后,延时单元和SA的数量相对固定(除非有些系数为0,SA会有所减少),因此FIR滤波器的实现复杂度主要决定于MBA的个数。
一个离散子项空间中的元素可以通过下式构建[4]:
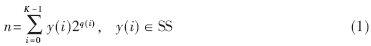

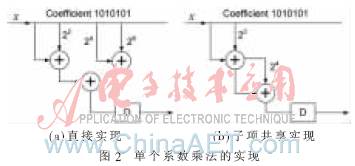
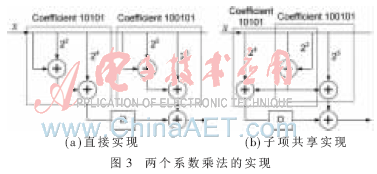
不论是单个系数内部,还是多个系数之间,用来实现公共子项的加法器都可以共享,从而达到减少加法器个数的目的。下面举例说明:(1)假设某个系数用二进制序列表示为1010101,如果直接实现,则需要3个加法器,如图2(a)所示;如果将公共子项101提取出来先实现,则只需要2个加法器,如图2(b)所示。(2)假设某两个系数用二进制序列表示分别为100101和10101,若两个系数独立实现,则每个系数都需要2个加法器,即总共需要4个加法器,如图3(a)所示;而将公共子项101提取出来先实现,则每个系数只需要增加1个额外的加法器,即总共需要3个加法器,如图3(b)所示。因此,合理利用子项共享,可有效降低数字滤波器的硬件消耗 [4]。
2 FPGA内部结构及综合特点
硬件描述语言HDL(Hardware Description Language)支持行为级(Behavioral Level)、寄存器传输级RTL(Register Transfer Level)和门级(Gate Level)3个不同级别的设计,目前普遍使用寄存器传输级源代码进行设计。综合是把设计转化为可制造器件的转移过程,而该器件能执行预期的功能。
FPGA是专用集成电路(ASIC)领域中的一种半定制电路,应用非常广泛,经常作为高阶数字滤波器的实现器件。Altera公司的FPGA器件一般由二维的行列结构来实现用户自定义逻辑,内部最小的逻辑单元LE可以高效地实现用户逻辑函数[10]。一个LE主要由一个4输入查找表、一个寄存器及进位和互连逻辑组成。查找表简称为LUT,LUT本质上是一个RAM。当用户通过原理图或HDL语言描述了一个逻辑电路后,FPGA开发软件会自动计算逻辑电路所有可能的结果,并把结果事先写入RAM,这样每输入一个信号进行逻辑运算就等于输入一个地址进行查表,找出地址所对应的内容后输出即可。也可以把LE当作一个4输入的函数发生器,能够实现4变量输入的所有逻辑[10]。由于RTL级设计不涉及具体的工艺,不同的综合工具、不同的器件类型可能会产生不同的综合结果,即所需要的LE数量会有差异。因此,在同一种综合工具、同一种器件类型的前提下对不同的实现方法进行比较。
3 基于Verilog HDL的RTL级实现
Verilog HDL是目前广泛使用的IEEE标准硬件描述语言,可以用不同的工具进行综合和验证。本文基于子项空间共享技术,采用Verilog HDL进行FIR数字滤波器的RTL级描述。下面举例介绍具体的实现方法。以参考文献[4]中的较低阶滤波器S1为例,下面给出滤波器S1的系数,其中,h(n)=h(24-n),13≤n≤24;通带增益为485.268 2。
h(12)=3×26-1×20;h(11)=5×25-1×24;h(10)=3×24;
h(9)=-3×23;h(8)=-1×25;h(7)=-3×20;h(6)=1×24;
h(5)=5×21;h(4)=-1×22;h(3)=-1×23;h(2)=-1×21;
h(1)=3×20;h(0)=1×21。
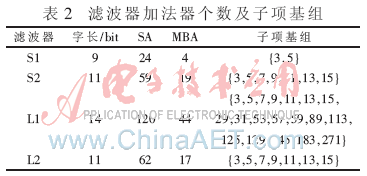
由上可知,S1对应基组为{3,5},此基组的阶数等于2,即产生基组需要2个加法器,由基组产生滤波器系数需要2个加法器,因此,MBA的个数为4,系数都不为零;SA的个数为24。
(1)子项基组的产生
assign x3={x_n,1'b0}+ x_n; //x_n为输入信号
assign x5={x_n,2'b00}+x_n;
(2)MBA的实现
利用已经产生的基组,参照S1的系数,就可以得到MBA部分各常系数乘法的值,部分程序段如下:
assign MBA12={x3,6'b000000}-x_n; //实现h[12]×x_n
……
assign MBA0 = {x_n,1'b0}; //实现h[0]×x_n
(3)延时单元和SA的实现
例S1中不存在值为0的系数,且考虑到线性相位FIR滤波器系数对称,因此程序段如下:
Delay_SA0 <= MBA0;
Delay_SA1 <= Delay_SA0 + MBA1;
……
Delay_SA11 <= Delay_SA10 + MBA11;
Delay_SA12 <= Delay_SA11 + MBA12;
Delay_SA13 <= Delay_SA12 + MBA11;
……
Delay_SA23 <= Delay_SA22 + MBA1;
Delay_SA24<= Delay_SA23 + MBA0;
(4)输出的实现
考虑到S1的系数在有限字长实现时单位脉冲响应乘以512(=29)倍,因此在输出时要进行截短处理,即去掉低9位。
4 综合结果
本节将选取参考文献[4]中的4个例子分别在FPGA上进行综合比较。4个例子的性能指标如表1所示。

参考文献[4]中基于子项共享进行系数离散化得到的结果如表2所示,具体的滤波器系数参见参考文献[4]。
如前所述,FPGA实现硬件资源的消耗可以通过综合后LE的数量来衡量。分别选择Cyclone系列的EP1-
C12Q240C8和APEX20KE系列的 EP20K600EBC652-3两种型号的FPGA对4个滤波器两种不同的实现方法(子项共享实现和直接实现)进行综合,综合工具选用Quartus II,结果如表3所示。
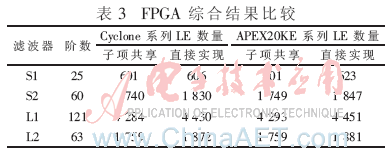
从表3可以看出,基于子项共享的实现可以有效减少FPGA中LE的消耗数量,且滤波器阶数越高,共享的机会越大,效果越好。
本文通过Verilog HDL编程在FPGA上实现了子项共享的FIR数字滤波器设计。子项空间共享技术可以有效地减少FIR滤波器实现时加法器的个数,从而使得综合后消耗的LE数量明显减少,有利于数字系统的低成本、低功耗设计,具有实际的应用意义。
参考文献
[1] 唐博,李锦明,李士照.基于FPGA的高阶FIR滤波器强抗干扰数据采集系统[J].电子技术应用,2012,38(9):89-92.
[2] 林志典,张方佩,袁国顺.基于FPGA的高速FIR滤波器的设计与实现[J].微电子学,2013,43(4):200-202.
[3] 惠鹏飞,姚仲敏,夏颖,等.基于FPGA的无线传感网络信道波形整形滤波器[J].电子技术应用,2013,39(7):35-37.
[4] YU Y J,LIM Y C.Design of linear phase FIR filters in subexpression space using mixed integer linear programming[J].IEEE Trans.Circuits Syst.I,2007,54(10):2330-2338.
[5] YU Y J,LIM Y C.Optimization of linear phase FIR filters in dynamically expanding subexpression space[J].Circuit Syst.Signal Process.,2010,29(1):65-80.
[6] SHI D,YU Y J.Design of linear phase FIR filters with high probability of achieving minimum number of adders[J].IEEE Trans.Circuits Syst.I,2011,58(1):126-136.
[7] POTKONJAK M,SHRIVASTA M B,CHANDRAKASAN A P.Multiple constant multiplication:Efficient and versatile framework and algorithms for exploring common subexpression elimination[J].IEEE Trans.Comput.Aided,1996,15(2):151-165.
[8] Xu Fei,CHANG C H,JONG C C.Design of low-complexity FIR filters based on signed-powers-of-two coefficients with reusable common subexpressions[J].IEEE Trans.Comput.Aided,2007,26(10):1898-1907.
[9] WANG Y,ROY K.CSDC:A new complexity reduction technique for multiplierless implementation of FIR filters[J].IEEE Trans.Circuits Sysm.I,2005,52(9):1845-1853.
[10] Altera公司.Cyclone2系列器件数据手册:Cyclone device handbook,volume 1[Z].2007.

