0 引 言

　　IIR滤波器不易做成线性相位，FIR滤波器只要满足一定条件就可做成线性相位，而现代图像、语声、数据通信对线性相位的要求是普遍的，因此具有线性相位的FIR数字滤波器得到广泛的发展和应用。

　　FIR滤波器有传统的设计方法，如窗函数法、频率采样法、切比雪夫逼近法等；之后也有一些优化设计算法，如Remez交换算法、线性规划算法、加权最小二乘法、递推最小二乘法。虽然这些算法在一定程度上改善了传统方法的局限性，但这些方法自身也存在着一些不足。之后，曾喆昭等人提出了一种基于余弦基神经网络的算法，给出了该算法的收敛条件，并将其应用到高阶多通带FIR滤波器中，用实例说明了该算法在精度、计算速度等方面的优越性。基于这种算法，有人分别将其在数域和维数上做出了推广。

　　本文提出的方法，是基于余弦基神经网络设计方法的一种改良，其基本思想首先是使设计频响与理想频响之间的全局误差在通带和阻带范围最小，其次再使用模拟退火算法，以最小阻带衰减为评价函数优化网络权值，使最后的结果朝着最优值靠近。由该方法设计的滤波器，通带和阻带范围无过冲、无波动，且阻带的衰减高，初始条件随机给定，算法速度快，因而是一种有效的设计方法。

　　1 I型线性相位FIR滤波器的幅频特性

　　若脉冲响应h(n)是实序列，且满足h(n)=h(N-1-n)，N为脉冲响应h(n)的长度，并且N为奇数，则有：

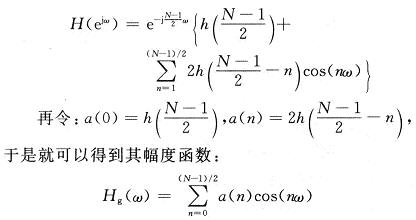
　　容易看出，此式是由(N+1)／2个余弦项迭加而成的函数，而此函数在ω=0，π，2π处均不等于零，因此I型线性相位FIR滤波器既可以用作低通滤波器(在ω=0处，幅度函数不为零)，也可用作高通滤波器(在ω=π处，幅度函数不为零)，而且也可以用作带通和带阻滤波器，是应用最为广泛的。

　　2 余弦基神经网络

　　在网络结构方面，如图1所示，类似于BP网络的结构：

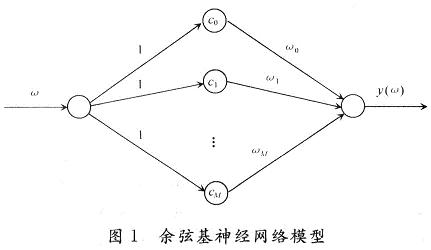
　　输入层和输出层都只有一个节点，隐含层有M个节点，且各节点对应的激励函数如下：

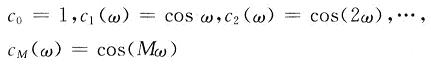
　　式中：M=（N-1）/2

　　再令输入层到隐含层的全值都为1，而隐含层到输出层的权值ω0～ωM分别取为a0～aM，于是神经网络的输入／输出关系就恰好为滤波器的幅度函数

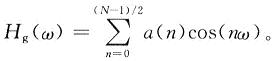
　　网络学习算法方面，也可以采用类似BP网络的学习算法。

　　首先定义权值矩阵：

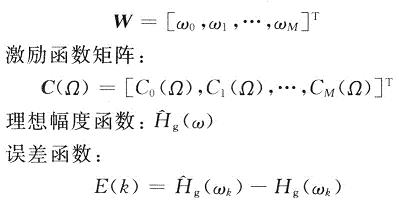
　　设置性能指标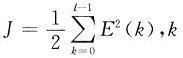：为训练样本数。

　　于是权值修正的公式为：

　　式中：α为学习速率。

　　迭代的终止条件可设为性能指标J满足一定条件，而关于学习速率α的选取会直接影响到神经网络的稳定性。目前，已经有人提出了其适当的选取范围，例如罗玉雄等人已经证明，当满足0<α<(2／|| C ||2)时(这里||·||2表示的是欧氏范数的平方)，神经网络是稳定的；曾喆昭等人也提出并证明了当满足0<α<(4／N)时，神经网络是稳定的。

　　3 模拟退火算法

　　由于以上的网络学习算法从本质上来说，还是一种BP算法，所以不可避免地会存在BP算法的缺陷，初始值的选取会影响最终结果，且容易陷入局部极小值。

　　模拟退火算法与初始值无关，算法求得的解与初始解状态(是算法迭代的起点)无关；模拟退火算法具有渐近收敛性，在理论上已得到严格证明，当初温充分高，降温足够慢，每一温度下抽样足够长，最终温度趋于零时，算法最终以概率1收敛到全局最优解。模拟退火算法通过概率判断来接受新状态是算法在局部极小解处有机会跳出并最终趋于全局最优的根本原因。于是将模拟退火算法加到前面的算法中去，就可以很好地弥补上述算法的不足。

　　模拟退火算法的步骤如下：

　　(1)由一个产生函数从当前解S产生一个位于解空间的新解S'。

　　(2)计算与新解所对应的目标函数差。这里以最小阻带衰减为评价函数C(S)，这个函数可以由所得解S轻易地求出，于是目标函数差△t=C(S')-C(S)；

　　(3)判断新解是否被接受，其依据是一个接受准则，最常用的接受准则是Metropolis准则。若△t≥0，则接受S'作为新的当前解S；否则，以概率exp(-△t／T)接受S'作为新的当前解S。

　　(4)当新解被确定接受时，用新解代替当前解，同时修正评价函数。此时，当前解实现了一次迭代，可在此基础上开始下一轮试验；当新解被判定为舍弃时，则在原当前解的基础上继续下一轮试验。

　　将模拟退火融入原算法，其实主要是用原算法来实现模拟退火中第(1)步的产生解S，于是可得到总的算法：

　　(1)初始化，初始温度T(充分大)，初始解状态S(是算法迭代的起点)，每个T值的迭代次数L，初始权值W，性能指标J，学习速率α，并且设定目标向量(理想幅频响应Hg(ωk))；

　　(2)对k=1，2，…，L做第(3)～(8)步骤；

　　(3)计算误差E(k)，使用权值修正公式：W=W+αE(k)C(Ωk)修正权值；

　　(4)满足性能指标J转步骤(5)，否则转步骤(3)；

　　(5)由步骤(4)产生的W得出新解S'；

　　(6)以滤波器的最小阻带衰减为评价函数，计算△t，其中△t=C(S)-C(S)；

　　(7)若△t>0，则接受S'作为新的当前解，否则以概率exp(-△t／T)接受S'作为新的当前解；

　　(8)如果满足终止条件，则输出当前解作为最优解，终止条件通常取为连续若干个新解都没有被接受；

　　(9)减小T，转步骤(2)。当T→0时，终止算法。

　　4 仿真实例

　　例1：设计一线性相位高通FIR滤波器，其理想幅频特性为：

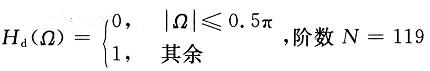
　　对Ω在[0，π]范围内均匀取样，共取(N+1)／2＝60个样点，即Ωk=πk／59(k=0，1，2，…，59)，为了使通带和阻带内无过冲、无波动，在过渡带内取两个点0．78和0．25，于是实际的幅频取样点为Hd(k)=[zeros(1，29)，0．25，0．78，ones(1，29)]；网络结构取为1×60×1，性能指标设置为J=10-8。

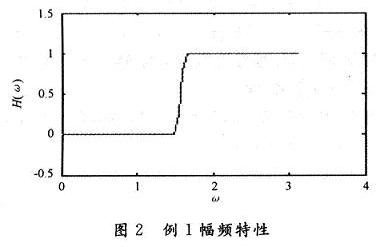
　　经过计算机仿真得到如图2和图3的仿真图。

　　例2：设计一线性相位带阻FIR滤波器，其理想幅频特性为：

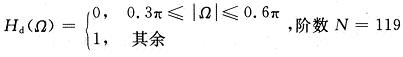
　　与例1类似，对Ω在[0，π]范围内均匀取样，共取(N+1)／2＝60个样点，即Ωk=πk／59，(k=0，1，2，…，59)，同样地，为了使通带和阻带内无过冲，无波动，在过渡带内取两个点0．78和0．25，于是实际的幅频取样点为Hd(k)=[ones(1，17)，0．78，0．25，zeros(1，16)，0．25，0．78，ones(1，23)]；网络结构取为1×60×1，性能指标设置为J=10-8。

　　经过计算机仿真得到如图4和图5的仿真图。

　　通过仿真，可以和与文献[2]中的算法相比较。在这里以例1中的情形为例，两种方法各运行10次，取最后得到的最小阻带衰减(单位：dB)和程序的运行时间(单位：s)来比较：

　　文献[2]中的算法：

　　两者相比较可得，虽然在运行时间上本文的算法逊于文献[2]中的算法，但这个运行时间本身也仅0．5 s左右，是可以接受的。在性能上本文的算法得出的结果几乎都在-190 dB左右，而文献E23中算法得出的结果则在-77～-93 dB之间波动，因此可以说用本文的算法可以得到更好、更稳定的最小阻带衰减。

　　5 结 语

　　本文提出了一种基于经优化算法优化过的神经网络设计FIR滤波器的方法。这一方法的特点是先用类似BP网络的方法调整神经网络权值，再用模拟退火技术进行优化，获取更好的FIR滤波器的脉冲响应，从而完成滤波器的设计。由文中给出的两个范例可以看出，设计滤波器的幅频响应在通带与阻带范围均无过冲现象，衰耗特性好，阻带最小衰减在190 dB以上，通带没有衰减。而且这种方法可以轻松地实现低通、高通、带通、带阻FIR滤波器的设计，程序运行时间均在0．5 s左右，是一种十分有效的设计方法。当然此算法也有改进的余地，比如在算法中过渡带的选取都是0．25和0．78。而事实上，对于不同的幅频特性，过渡点的选取可影响到最终设计的FIR滤波器的性能。通过优化过渡点的位置，可以使FIR滤波器的幅频特性在过渡点处更为平滑，并且有更好的最好阻带衰减。比如在文献[9]中，就有用遗传算法优化过渡点的方法。