优化网格环境下任务调度的近视眼算法
2008-03-21
作者:赵 颖1,蔡 伶2,周艳会1
摘 要: 任务调度" title="任务调度">任务调度是网格计算" title="网格计算">网格计算的关键技术之一,其作用是根据当前网格系统的负载情况,对系统内的任务进行调度,以提高系统运行效率。在普通任务调度算法的基础上,提出了近视眼任务调度算法,并通过性能分析得出近视眼调度算法在计算复杂度上优于普通算法的结论。
关键词: 网格计算 任务调度 近视眼算法
网格即一个集成的计算与资源环境,能够充分吸纳各种计算资源,并将它们转化成一种随处可得、可靠、标准且经济的计算能力。所谓计算资源,除了各种类型的计算机,还包括网络通信能力、数据资料、仪器设备、甚至人等各种相关的资源[1]。网格计算(Grid Computing),则是基于网格的问题求解,实现对丰富的网络资源和繁多的网络节点的管理,让它们形成一个有机整体,从而发挥最大效益。
网格的出现,代表了一种先进的技术和基础设施,最终给使用者带来了与地理位置无关、与具体的计算设施无关的通用计算能力。因此,网格堪称Internet之后网络领域又一次重大的科技进步。
当前,高性能任务调度技术、高吞吐率管理技术、数据收集分析、可视化技术以及安全技术,是网格的核心服务技术。核心服务是连接网格底层与高层功能的纽带,是协调整个网格系统有效运转的中枢。因此对核心服务技术的研究具有非常重要的意义。
本文通过深入研究任务调度技术和算法,在常用任务调度算法的基础上提出另外一种算法,称为近视眼算法" title="近视眼算法">近视眼算法。与普通算法相比,对于给定完成期限和资源需求的任务调度具有相同的结果,但在计算花销上有明显提高。
1 任务调度
通常情况下,网格系统中运行着大量的应用,这些应用共享网格的各种资源。如何才能使并行运行、共享资源的应用获得最大效能,这正是任务调度需要解决的问题。
任务调度的目的是在包含大量不同资源的网格环境" title="网格环境">网格环境中,把不同的任务以最合理的方式分配到相应的网格节点上去完成。为了对网格计算环境中的资源充分利用和优化,需要合理、透明地在处理机之间分配任务,以使系统的综合性能最高。任务调度应用到的几个概念具体解释如下:
(1)节点:表示网格环境中具有计算能力的实体,拥有处理器(Processor)和其他资源(Resource),这些资源可以是除处理器外的任何资源。
(2)任务:可以被分配到计算节点上的实体,可以是进程、子函数或线程等。
(3)任务集合:所有需要调度的任务。
(4)任务调度算法:任务调度的实现算法,就是找到一种从任务到节点的映射。
调度问题一般可分为两大步骤:第一步是在空间上对计算和数据进行分配,包括选取给定任务所需要的资源组合,将任务交给这些资源去执行,并分配相关的数据和计算等;第二步就是在时间上为计算和通信进行排序,包括在计算资源上为不同的任务进行排序,同时为不同任务之间的通信进行排序等。
与传统高性能计算的调度策略和技术相比,网格调度更加复杂,任何一个网格调度器都无法对所有的网格资源进行管理,而且网格资源是不断动态变化的。因此,网格的调度需建立随时间变化的性能预测模型,充分利用网格的动态信息来表示网格性能的波动。由于网格还具有异构性和多样性特征,所以网格的调度还必须考虑到多种多样的环境和条件。
目前,网格计算中的任务调度算法主要有局部和全局、最优和近优、静态和动态、自适应算法等几种。
由于绝大多数最优调度问题都是NP完全问题,所以实际的解决方案往往是进行非最优调度,即近优方案,相关算法有解空间枚举和搜索算法等,但它们具有很大的计算量。依靠启发式方法寻求近优解是更加优化的方法。所谓启发式方法,是指能够根据系统反馈动态调整调度,向优化的方向调整调度行为。本文提出的近视眼算法正是结合启发式函数的近优任务调度算法。
2 近视眼算法的任务调度模型
任务调度问题的实质是,在一个有N个需要调度的任务、M个可用的任务执行单元(网格节点)和i个数据储存单元构成的网格环境下,把N个任务Task={T1,T2,…,Tn}以合理的方式调度到M个节点Host={h1,h2,…,hm}上去执行,目的是通过调度使执行时间尽可能短。
2.1 术语
(1)可行(feasible):在调度中一个任务是可行的,表示调度算法可以满足此任务所需的时间限制和资源需求,即可以调度。一个任务集合是可行的,表示任务集合中所有任务都是可行的。
(2)部分调度(partial schedule):部分调度是指任务集合的一个子集是可行的。
(3)强可行(strongly feasible):称一个部分调度是强可行的,是指从任务集合的未调度任务中任取一个,对部分调度进行扩展,得到的部分调度都是可行的。
(4)最早有效时间EAT(Earliest Available Time):某个资源可以共享使用或排他使用的最早时间。
2.2 条件
近视眼算法所在的任务调度模型通过以下属性来标志一个任务:
最早到达时间:Ta(Task arrival time)
最早开始时间:Test(Task earliest start time)
处理时间:Tp(Task processing time)(处理任务所需要的时间间隔)
任务资源需求:Tr(Task resource requirements)
任务完成时限:Td(Task deadline)
调度过程中,算法通过任务的最早到达时间Ta和网格环境中的资源信息决定任务的最早开始时间Test。对于一个可行的调度来说,每个任务都应该满足如下条件:
0≤Ta≤Test≤Td-Tp
一个任务在运行时需要诸如文件、外设、数据结构、变量、通信缓冲等不同资源。对任意一种资源可以有两种访问方式:
(1)排他使用,不允许其他任务和此任务共同使用同一资源。
(2)共享使用,如存在其他任务需要共享使用同一资源,则允许其共同使用。
如果同时存在任务TASKi和TASKj,并且排他使用同一资源,就会发生资源冲突,这时某一任务必须等待,直到资源可用。本调度模型规定,任务是不可剥夺的,即任务被调度算法分配到某一节点后,将一直运行到完成为止。
3 近视眼算法描述
3.1 术语
给出算法描述之前,先定义几个术语:
(1){剩余任务}:还没有被调度的任务,可按照任务的某种属性顺序存放,以方便调度。
(2)Nr:{剩余任务}中的任务个数。
(3){应调度任务}:{剩余任务}中的前k个任务,又称为可行性检测窗口。
(4)k:用于调度算法的任务最大数,也就是扩展部分调度时,对剩余任务队列中的k个任务进行比较,得到具有最小启发函数" title="启发函数">启发函数值的任务。也可称为可行性检测窗口的大小。
(5)Nk:检测窗口中实际的任务个数,大多数情况下等于k,当剩余任务个数小于检测窗口时Nk=Nr,即Nk=min(k,Nr)。
3.2 启发函数
近视眼调度算法使用启发函数H集成任务的各种属性。通过控制启发函数,达到根据任务的不同属性要求进行调度的目的,从而更加切合实际。
例如,有的调度要求调度时间严格一些,有的调度要求资源需求重要一些等等。当对未调度任务进行调度扩展时,将启发函数应用到这些将要进行调度的任务上,并且选取启发函数值最小的任务进行扩展。
下面是几个常用的启发函数:
最小完成时限优先(minimum deadline first:Min_D):H(T)=Td;
最小处理时间优先(minimum processing time first:Min_P):H(T)=Tp;
最小最早开始时间优先(minimum EST first:Min_S):H(T)=Test;
最小松弛优先(minimum laxity first:Min_L):H(T)=Td-(Test+Tp);
Min_D+Min_P:H(T)=Td+W*Tp;
Min_D+Min_S:H(T)=Td+W*Test;
前四个是简单启发函数,后两个是复合启发函数。其中,Min_D+Min_P综合考虑完成时限和处理时间的因素,Min_D+Min_S 综合考虑完成时限和任务所需要的资源。W是复合函数中组合两个简单启发函数的权重,通过修改权重可以根据任务的不同需求进行调度。
因为最小完成时限优先和最小处理时间优先没有考虑到任务的资源需求,所以近视眼调度算法中采用Min_D+Min_S作为启发函数。这样,既考虑了任务本身的特征,又考虑了任务的资源需求。
3.3 算法描述
对任务集合进行调度从而发现一种可行性调度的过程类似于一个查找的过程。任务集合中的任务构成一棵查找树,从查找树顶点开始的子树对应部分调度,整棵树对应完全调度。要找到一个可行性调度,最基本的方法是穷举遍历,例如深度优先、广度优先等,但计算复杂度太高。在很多实际应用中,时间要求是很严格的,因此需要一种更快的调度算法。
近视眼算法使用如下方法确定一个任务集合的可行性调度。从查找树的根结点开始,将根结点从查找树中移出扩展调度,依次对所有任务进行扩展,直到发现完全可行性调度。
在调度过程中,对部分调度进行扩展前,首先判断部分调度是否是强可行的,若使用任务T对部分调度进行扩展不是强可行的,说明这种情况下完全调度不可行。这时,可以采用回退的方法,返回到上一次任务调度,继而使用另外一个任务而不是使用任务T对调度进行扩展。
第二次被选择的任务应该是具有次大启发函数值的任务。虽然算法中允许回退操作,但对回退次数应该限制,以保证算法的效率。回退限制可以通过设置最大回退次数,或者设置启发函数值限制来实现。
总结上述思想,得出近视眼算法的工作步骤如下:
第一步:按照某一属性将任务插入到任务队列中,初始化部分调度,例如可以按照任务的完成期限Td升序存放集合中的任务。
第二步:根据可行性检测窗口(任务队列的前k个任务),判断调度算法当前步骤中部分调度是否是强可行的。
第三步:如果是强可行的,则对检测窗口中的任务应用启发函数H(T)=Td+W*Test得到每个任务的启发函数值,选取具有最小值的任务对部分调度进行扩展;否则,将算法回退到上一步骤,选取启发函数值次大的任务对部分调度进行扩展。
第四步:重复第二步和第三步,直到以下情况出现:
(1)发现完全可行性调度;
(2)到达最大回退次数或者到达启发函数限制值;
(3)不能再回退。
4 近视眼调度算法性能分析
4.1 任务调度仿真系统
通过对任务调度系统进行仿真,实现启发式函数和近视眼调度算法,从而对算法进行性能分析。仿真系统主要包括任务生成器、资源生成器和任务调度器三个部分:
(1)任务生成器:按照用户输入的参数产生任务集合。
(2)资源生成器:生成调度所需要的资源。
(3)任务调度器:利用任务生成器产生的任务和资源生成器产生的资源进行调度,从而发现一个完全可行性调度。
仿真系统的参数设置界面如图1所示。
用户可在这里设置系统仿真时的任务生成器、资源生成器和任务调度器的参数。设置完毕,就可以按照参数对系统进行初始化,继而实现任务调度的仿真。
4.2 仿真实验结果
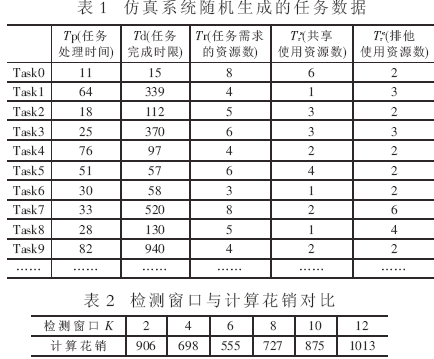
仿真系统通过设置检测窗口的大小得到近视眼调度算法的计算花销。计算花销是指调度过程中主要的比较计算的次数,包括检测窗口对任务启发函数值的排序,对具有最小启发函数值的任务进行部分调度扩展时的比较计算的次数以及任务发生回退而重新调度时进行比较计算的次数。
例如,任务数为50,节点数为5,实验结果数据如表1和表2所示。
从实验数据可以看出,随着检测窗口大小的改变,任务调度的计算花销也随之改变。当检测窗口值为6~8时,计算花销处于最小值状态,近视眼算法在计算复杂度上优于普通算法。随着检测窗口的增大,对窗口中任务的启发函数值排序的花销逐渐增大,检测窗口大小一直增大到等于任务集合的大小时,近视眼算法就退化为普通调度算法。
4.3 性能分析
普通调度算法首先判断部分调度是否强可行,如果是,则对所有剩余任务应用启发函数找到具有最小启发函数值的任务,从而对部分调度进行扩展。它对强可行的判断是基于所有剩余任务进行的,算法实质是对任务集进行递归遍历。
相反,近视眼算法中,判断是否强可行只是对剩余任务中的前Nk个任务(这里的0≤Nk≤k)进行的。近视眼算法在保证任务可调度的情况下,可降低递归遍历的深度,从而降低了算法的时间复杂度。
假设任务集合中有n个任务,普通调度算法的计算复杂度可以表示为O(n2),而近视眼算法在调度的每一步骤中只考虑Nk个任务,复杂度为O(nk),这里Nk≤k,近视眼算法的复杂度与任务集合中的任务个数为线性关系。
在调度的每一步只考虑前Nk个任务,就好比近视的人只看到最近的物体,因此把这种算法形象地命名为近视眼算法。而可行性检测窗口的大小,也就是近视程度,在整个算法中起着关键作用,正是它提高了调度的整体性能。
参考文献
1 都志辉,陈 渝,刘 鹏.网格计算.北京:清华大学出版社,2002
2 W Allcock,A Chervenak,I Foster et al.The data grid:towards an architecture for the distributed management and analysis of large scientific datasets.Journal of Network and Computer Applications,2001;(23)
3 Jason Leigh,Thomas A.DeFanti,Andrew E Johnson.Global Tele-Immersion:Better than Being There.in:proceedings of 7th International Conference on Artificial Reality and Tele-Existence,Tokyo,Japan,Dec,1997
4 Johnson A E,Leigh J,DeFanti T.Multi-Disciplinary EXPE-RIENCES with CAVERN soft Tele-immersive applications.in:Proc.of Fourth International Conference on Virtual System and Multimedia,November 1998
5 I Foster,C Kesselman,J Nick.The physiology of the Grid,Global Grid Forum,2002
6 Kavitha Ranganathan,IanFoster.Identifying dynamic replication strategies for a high performance data grid.in:Proceedings of the International Grid Computing Workshop,2001
7 Ritchie G,Levine J.A fast,effective local search for scheduling independent jobs in heterogeneous computing environments.In:Proceedings of the 22nd Workshop of the UK Planning and Scheduling Special Interest Group,2003