蓄电池用途极其广泛，对其研究也一直在进行，监控技术是该领域的关键技术之一，特别是近年来随着电动汽车、储能技术的发展，蓄电池监控技术越来越显得重要，俨然成为各大设备厂商竞争的核心技术之一。准确检测蓄电池的荷电状态SoC(State of Charge)、劣化情况、健康状态等，及时对蓄电池系统进行维护、避免损失是其意义所在。

    阀控铅酸蓄电池(VRLA)诞生于1970年，之后的几十年时间里，人们对蓄电池的工作原理，工作性能，维护保养等方面进行了大量的研究，常用的方法有安时积分法^[1]，开路电压法，阻抗分析法，Peukert定律，密度法等，近年来人工智能算法也开始吸引了大量关注。

    参考文献[2]对铅酸电池的SoC预测进行了研究，在单片机上实现了基于蓄电池电动势和内阻的电量模糊预测。参考文献[3]应用模糊神经网络对MH/NI电池进行SoC预测，建立了四层结构网络。参考文献[4]采用无味卡尔曼滤波算法对锂电池的SoC进行估计，将电池开路电压(OCV)作为参数。参考文献[5]给出了利用采样点卡尔曼滤波进行电池SoC估计的具体步骤，该模型用电池电压，电流和温度作为参数。面向应用，参考文献[6]以MSP430单片机为核心控件设计了面对一体化壳体的低功耗电容式电子测压器。

    本文建立了基于神经网络的电池荷电状态的预测模型，在模型中考虑到内阻、放电电压、温度、放电电流等多参数对蓄电池的SoC进行预测，设计并制作了硬件，通过实验验证本文提出方法对工程应用的指导意义。

1 蓄电池荷电状态预测模型

    ANFIS(Adaptive Neuro Fuzzy Inference System)是一种自适应神经网络，具有神经网络的学习能力，而功能又与模糊推理系统等效。其隶属度函数参数和结论参数可以通过数据的训练来自主确定和更新，所以ANFIS适用于特性难以掌握的复杂系统的建模^[7]。ANFIS采用Takagi-Sugeno推理计算方法,结构为一阶：

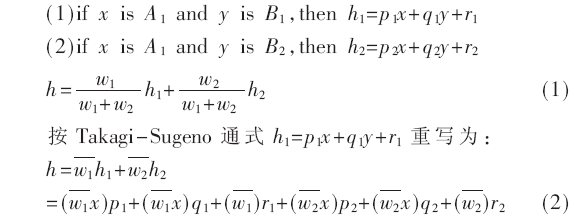
    自适应网络的学习规则是基于梯度下降和链式法则^[8]，由于梯度方法收敛缓慢且易陷入局部最优，ANFIS采用混合学习规则加速学习进程。

    电池SoC取决于多个因素^[8]，SoC可表示为:

其中，V_bat(t)和I(t)为测试变量，R_Ω(θ)由实验测定，时间常数τ_d和τ_k通过实验数据和仿真测试。R_k(θ)和R_d(θ)由最小二乘算法拟合曲线得到。

    本文建立的ANFIS模型的输入参数确定为内阻R，放电电压V，温度T、放电电流I。实验测得，放电过程中，电池内阻变化范围为3.8 mΩ～6.3 mΩ，即论域为[3.8，6.3]，将其划分为m个模糊集：R₁，R₂，…，R_m。电压变化范围为12.5 V～10.5 V，即论域为[12.5，10.5]，划分为n个模糊集：U₁，U₂，…，U_n。取温度变化范围为5 ℃～20 ℃，划分为p个模糊集：T₁，T₂，…，T_p。放电电流取值范围为5 A～25 A，划分为q个模糊集：I₁，I₂，…，I_q。Sugeno模糊模型采用式(8)所示局部线性函数形式的模糊规则。

    建立了基于ANFIS的一个4输入、1输出的系统，如图1所示。

    第1层是输入层，它将输入模糊化，将4个论域分别划分为m、n、p、q个模糊集。各节点输出相应隶属度函数的值。

其中K₁，K₂，K₃，K₄取值分别为1～m，1～n，1～p，1～q。采用复合T规范的AND乘法算子确定每条规则的激励强度。第3层中每个节点都是圆形的，计算第i个规则的激励强度相对于所有规则激励强度的和的比值，本层输出称为归一化激励强度：

2 嵌入式系统设计

2.1 实验原理

    本文建立的ANFIS模型，需大量实验数据对网络模型进行训练、校验和验证，实验原理为：(1)获取不同条件下阀控式铅酸蓄电池放电数据；(2)将获取的数据用于训练和检验模型；(3)验证训练完成后模型的预测精度和有效性。根据验证情况对模型进行改进，再次验证。

    监测系统在嵌入式平台中实现，实验结果及软件中各参数标定为系统软硬件设计提供参考。

2.2 硬件设计

    硬件系统含测量单元和显控平台两部分，如图2所示。前者用于测量内阻、电压、输出电流、温度，实现简单的插值运算及与显控平台通信。测量单元基于单片机设计，采用STC12C5A60S2。后者采用ARM Cortex-A8 Samsung S5PV210。

2.3 内阻测量电路设计

    本文采用交流注入法测量蓄电池内阻，用频率为1 kHz的交流恒流信号注入蓄电池，获取反馈并进行调理送入ADC采样。原理框图如图3所示。

2.4 内阻测量原理

    设信号发生器产生正弦信号I=Asinωt，由于电池的阻抗R_z存在容性成分，反馈信号与激励信号有相位差，设差分放大器的增益为B，则采样信号经过差分放大器后的值为：

3 仿真分析及相关实验

3.1 仿真分析

    建立4种ANFIS模型，模型1用钟型函数作隶属度函数，用genfis1产生初始FIS；模型2用高斯函数作隶属度函数，用genfis1产生初始FIS；模型3用减法聚类法函数genfis2产生初始FIS；模型4用模糊C-均值聚类法函数genfis3产生初始FIS。目标误差0，步长0.01，步长增长率和下降率分别为1.1和0.9，训练次数100。各模型原始实测数据与预测曲线及误差曲线如图4所示。

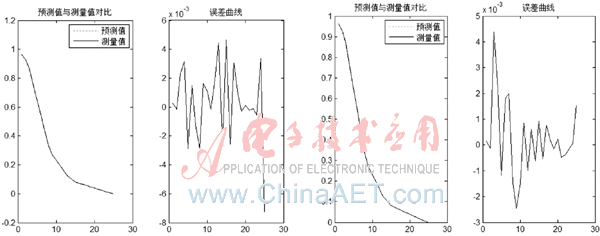
                         (a)模型1                               (b)模型2

                        (c)模型3                                 (d)模型4

图4  模型曲线对比图

    各模型的预测曲线与实际测量曲线重合度较好，其均方根误差最大值分别为0.007 3、0.004 4、0.007 4、0.006 0。结合应用需求，最适合用于预测蓄电池电能的是模型3。

3.2 设备实测

    系统从蓄电池满电开始放电，测量单元不断采集蓄电池的内阻、电压、电流、温度参数，发送给显控单元，显控单元通过ANFIS算法预测蓄电池容量。抽取间隔较大的10组数据如表1所示。

    表1所获得的数据是显控单元通过RS422与测量单元通信获得的，与实测值比较，各参数的误差均在5%以内。本系统的最终目的是将测量单元获得的数据输入显控单元的ANFIS算法程序中预测蓄电池SoC，因此表2对预测值与实际值进行了比较。

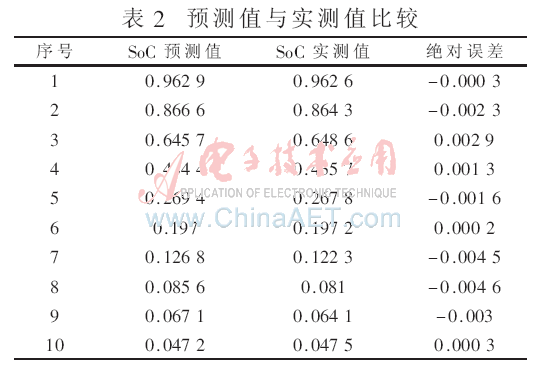
    从表2中可以看出，预测值与实际值的误差非常小，最大绝对误差为0.004 6，完全能满足工程应用需求。

    本文建立了ANFIS模型，完成了相关实验和仿真训练，设计了系统硬件和软件，分析了实际运行效果。实验证明用减法聚类法产生的ANFIS网络最优，节点数相对较少，预测效果好。

参考文献

[1] 李哲，卢兰光，欧阳明高.提高安时积分法估算电池SoC精度的方法比较[J].清华大学学报(自然科学版)，2010，50(8)：1293-1296，1301.

[2] 李智华，张青春，刘振.蓄电池剩余电量的模糊预测[J].上海大学学报(自然科学版)，2009，18(4)：364-368.

[3] 张梅.基于模糊神经网络的MH/Ni电池荷电状态预测[J].电源技术，2012，36(9)：1316-1318.

[4] 柏庆文.基于无味卡尔曼滤波的电动汽车动力电池SoC估计[D].长春：吉林大学，2013.

[5] 高明煜，何志伟，徐杰.基于采样点卡尔曼滤波的动力电池SoC估计[J].电工技术学报，2011，26(11)：161-167.

[6] 王亚军，李新娥，马英卓，等.一体化壳体电容式电子测压器的低功耗设计[J].电子技术应用，2012，38(8)：93-95.

[7] 艾芳菊.模糊神经网络的结构优化研究[D].成都：中国科学院研究生院（成都计算机应用研究所），2006.

[8] WERBOS P J.Beyond regression：New tools for prediction and analysis in the behavioral sciences[D].Boston：Harvard University，1974.