自然风速的随机性和风电机组的强非线性使风机输出功率不稳定。风速低于额定值时，机组的控制目标为最大风能捕获^[1]；风速高于额定值时，通过桨距角的调节，改变风能利用系数，使输出功率恒定^[2]。参考文献[3]采用微分几何将风电模型线性化再结合H∞控制理论设计恒功率控制器，参考文献[4]将微分几何线性化与极点配置结合设计变桨距控制器。此外，滑模变结构^[5]、自抗扰^[6]、自适应模糊^[7]等也在风电系统中得到应用。本文将精确反馈线性与模糊理论有机结合，设计变桨控制器并仿真，结果表明，该控制器能有效、迅速地稳定不确定风电系统，性能良好。

1 风电机组模型

    风力机模型：

其中：

    由(1)、(5)可知该风力发电系统的数学模型为：

    当风速在额定值之上时，控制目标是输出恒功率。把风机角速度的变化作为控制器的输入，在变桨距控制器的作用下改变桨距角，从而改变风能的利用系数，将风力机的转速控制在额定值附近，则输出功率限定在额定值。风力发电系统的变浆距控制框图如图1所示。

2 基于微分几何的风电系统全局线性化

2．1 精确反馈线性化理论^[8]

    单输入单输出的仿射非线性系统：

    则系统(6)被转化为：

3 模糊控制器的设计

    由式（14）知这是一个两输入单输出的系统。在该系统中，状态量z₁的物理含义为风力机的转速ω_r，z₂的物理意义为ωr的变化率所以模糊控制器的输入即为风力机实际转速与额定转速的误差e及误差变化率ec，输出为控制定律v。

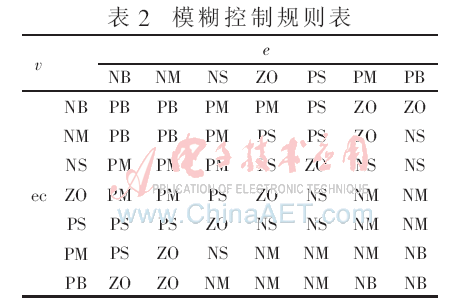
    误差的变化范围为[-0.5，0.5]，令语言变量E的论域X＝{-3，-2，-1，0，1，2，3}，从而e的量化因子K_e＝6。为语言变量E选取7个语言值分别为NB、NM、NS、ZO、PS、PM、PB，由经验可得出相应隶属函数，从而可得出语言变量的赋值表如表1所示。

    设ec的范围为[-0.06，0.06]，选EC的论域Y＝{-3，-2，-1，0，1，2，3}，则得误差ec的量化因子K_ec＝50。同时语言变量EC也选取7个语言值为NB、NM、NS、ZO、PS、PM、PB，则其语言变量EC的赋值表与E的相同，即表1所示。

    设v的范围[-3，3]，令V的论域Z＝{-3，-2，-1，0，1，2，3}，则v的比例因子K_v＝1。为语言变量V也选取7个语言值分别为NB、NM、NS、ZO、PS、PM、PB，则其语言变量的赋值表与EC和E的相同，即表1所示。

    对所有变量赋值后，下一步是模糊控制表的编写。根据风机角速度的误差及误差的变化率来确定控制器的输出。

    若风机角速度的误差与角加速度的误差变化趋势相同，都为正大或正中（小），意味着风机角速度有继续变大的趋势，所以控制器应输出负大或负中，以减小角速度的误差，使之趋于额定值。同理，若风机角速度的误差及误差变化率都为负大或负中（小），则控制器输出应为正大或正中。

    若风机角速度的误差与其角加速度的误差变化趋势相反，即角速度为正（负）而角加速度为负（正）时，可以看出系统本身已经向平衡状态调整，所以分别取较小的控制量。尤其当两者一个为正大（中、小），而另一个为负大（中、小）时，控制量取为0。

    若风机角速度误差与角加速度的误差其中有一个为0，则系统必在稳态附近，所以控制量取较小的值。

    由以上分析得到模糊控制表如表2所示，可得原系统的非线性模糊变桨距控制器。

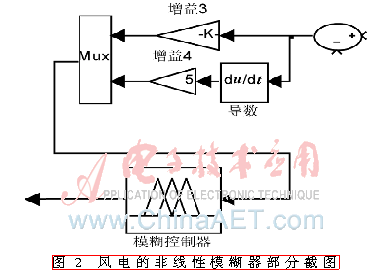
4 结果与分析

    如图2所示，在MATLAB/Simulink中建模并仿真，结果如图3和图4所示。

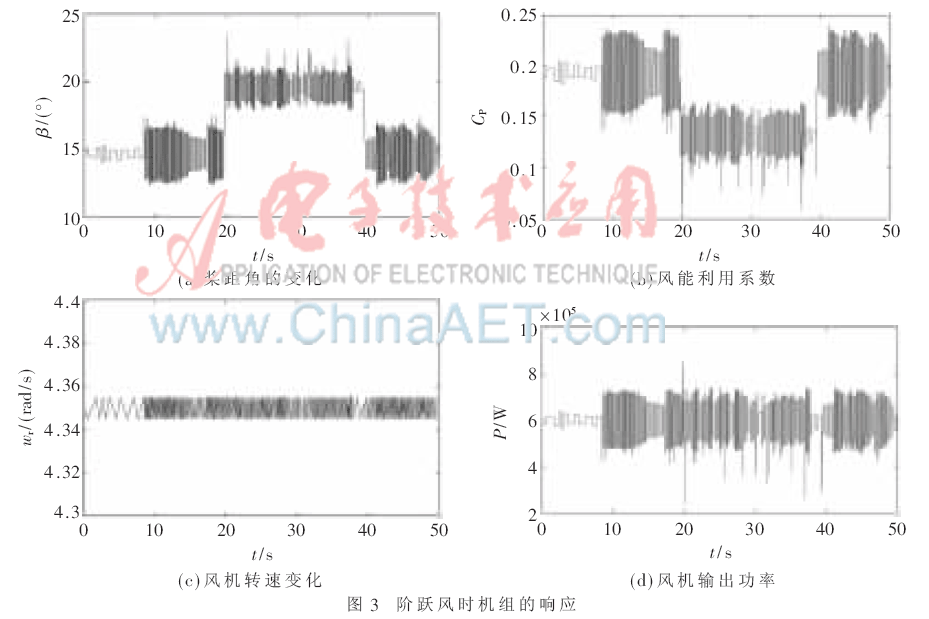
    (1)风速在15 m/s～17 m/s之间阶跃变化时的机组响应如图3所示。由图3可以看出，当风速阶跃增大时，桨距角也发生相应变化，从15°增加到20°左右。同时风能利用系数减小了，从0.2减到0.13左右，从而减少了系统风能的捕获，将风机角速度限定在4.35 rad/s，同时系统功率限定在600 kW左右。

    (2)风速在15 m/s～16 m/s之间随机变化时的机组响应如图4所示。由图4可知，在随机风速下，控制器也能将输出功率控制在额定值600 kW左右，实现了控制功能。

    本文利用微分几何原理对强非线性风电模型进行精确反馈线性化，再结合模糊理论，设计了模糊控制器。在MATLAB中建模并仿真，可知当风速在额定值以上变化时，控制器能通过调节桨距角来改变风能利用系数，使风机的角速度和系统功率稳定在恒值附近，体现了该模糊变桨距控制器的良好性能。但该控制器无法将输出功率严格稳定在600 kW，故还需改进。

参考文献

[1] 王琦，陈小虎，纪延超，等.基于双同步坐标的无刷双馈风力发电系统的最大风能追踪控制[J].电网技术，2007，31(3)：82-87.

[2] 叶杭冶.风力发电机组的控制技术[M].北京：机械工业出版社.2006

[3] 秦生升，胡国文，顾春雷，等.风力发电系统的恒功率非线性H∞鲁棒控制[J].控制理论与应用，2012，29(5)：617-622.

[4] 杨俊华，郑俭华，杨梦丽，等.变桨距风力发电机组恒功率反馈线性化控制[J].控制理论与应用，2012，29(10)：1365-1370.

[5] 郭庆鼎，赵麟，郭洪澈.1MW变速变距风力发电机的滑模变结构鲁棒控制[J].沈阳工业大学学报，2005，27(2)：171-174，186.

[6] 夏长亮，宋战锋.双馈风力发电系统转子电流自抗扰控制[J].电工电能新技术，2007，26(3)：11-14，19.

[7] 张新房，徐大平，吕跃刚，等.大型变速风力发电机组的自适应模糊控制[J].系统仿真学报，2004，16(3)：574-577.

[8] 卢强，孙元章.电力系统非线性控制[M].北京：科学出版社，2008.