摘  要： 在最大频繁项集的挖掘过程中，尤其在数据规模庞大并且最小支持度较小的情况下，超集检测成为算法运行的主要时间消耗，提出最大频繁项集算法A-MFI，其通过优化基于投影的超集检测机制有效地减少了超集检测的时间。另外，将事务数据库数据映射至一种压缩的AFOPT-tree结构，该结构结合自顶向下的遍历策略，具有更小的时间开销。

　　关键词： 最大频繁项集；关联规则；超集检测；最大频繁项集投影

　　1993年AGRAWAL R等人提出了一个重要的反映大规模数据中项目集之间有趣的关联或相关联系的研究课题[1]，找出属性间有价值的关系，即关联规则的研究。频繁项集的挖掘是获取关联规则不可或缺的步骤。但挖掘频繁项集时需要考虑太多的候选项集。最大频繁项集中已经隐含了所有的频繁项集，并且在许多数据挖掘应用中也只需要挖掘最大频繁项集，而不是获取所有的频繁项集，因此对最大频繁项集的挖掘具有重大的现实意义。

　　已有的最大频繁项集挖掘算法可以按照对搜索空间树的遍历策略分为宽度优先算法和深度优先算法两种。其中，MaxMiner、DMFI和DMFIA为宽度优先算法。MaxMiner[2]采用传统的横向数据集来计算频繁项集的支持度，虽然动态排序的方法能保证高效的前瞻剪枝，但扫描次数与Apriori[3]算法相同，扫描数据集的次数等于最长频繁项集的规模。GenMax、SmartMiner、Fp-Max和FPMFI是挖掘最大频繁项集的深度挖掘算法。算法GenMax[4]使用差集的方式表示事务数据库，在稀疏事务数据库的情况下有效减少了内存开销，并提出使用局部最大频繁项集的方式进行超集检测。SmartMiner[5]算法使用尾信息进行数据挖掘，不需要超集检测，但尾信息数据结构建立和访问代价太高。Fp-Max[6]算法也是基于Fp-tree的最大频繁项集挖掘算法，并将最大频繁项集保存在MFI-tree[7]中，在一定程度上提高了挖掘效率。

　　本文提出的A-MFI（Ascending Frequency Ordered Prefix-tree For Maximal Frequent Item Set）算法通过对基于投影超集检测方法[8]的优化，有效地提升了超集检测的效率；并采用AFOPT-tree（Ascending Frequency Ordered Prefix-tree）[9]来存储数据挖掘的相关信息，有效地减少了自顶向下遍历的时间开销和递归次数[10]。

　　1 相关知识

　　1.1 频繁项集和最大频繁项集

　　设I={i1，i2，i3，…，in}是一个项目集合，给定事务数据库D，对于项目集X?哿I且k=|X|，称X为k项集，或者简称为一个项集。记D为事务T的集合且T?哿I。对于给定的事务数据库D，定义X的支持度为D中包含X的事务个数，记为Sup（X）。用户自定义一个小于|D|的最小支持度，记为min_s。

　　定义1 给定书屋数据库D和最小支持度min_s，对于项集X?哿I，若Sup（X）≥min_s，则称X为D中的频繁项集。

　　定义2 给定事务数据库D和最小支持度min_s，对于项集X?哿I，若Sup（X）≥min_s并且对于任意（Y?哿I∧X?哿Y）均有Sup（Y）≦min_s，则称X为D的最大频繁项集。

　　性质1 任何频繁项集的真子集都不是最大频繁项集。

　　1.2 频繁模式树AFOPT-tree

　　Liu Guimei等提出使用一种称为AFOPT-tree[9]的数据结构来存储数据库中与当前挖掘过程相关的频繁信息。AFOPT-tree中每个结点对应一个项。树中每一条从根结点到某个子孙结点的路径表示一个项集，每个结点记录了根结点到该结点的路径对应项集的支持度。由于某些项集前部项的重叠，AFOPT-tree可以通过共享这些重叠的项来达到压缩保存的目的。

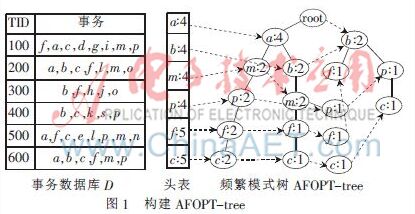
　　AFOPT-tree中有头表，头表中的频繁1-项集按照频繁次数的升序排列，它记录了相应频繁项的名称和支持度。AFOPT-tree树体中相同项的指针链接在一条链表上，链首指针也保存在头表中。数据库中的各项事务项集也按照头表中的次序添加到频繁模式树中。给定一个事务数据库D，与其对应的AFOPT-tree如图1所示。AFOPT-tree的建立需要扫描两次数据库，AFOPT子树的建立需要扫描两次搜索空间中结点的AFOPT子树中相应的条件模式基[10]。

　　2 基于AFOPT-tree的最大频繁项集挖掘算法A-MFI

　　2.1 优化的基于投影的超集检测

　　AFOPT-tree的头表和加入的事务项集都是按照频繁次数的升序排列的，按照头表中频繁1-项集的顺序挖掘出的频繁项集若存在超集，则必定在已挖掘到的最大频繁项集中[11]。

　　MFI即最大频繁集，是所有的最大频繁项目集组成的集合。MFI-tree是类似于AFOPT-tree的树形结构，用来存储最大频繁项集。从根节点到叶子节点的一条路径就是最大频繁项，中间节点不记录支持度，只有叶子节点记录支持度数。这里将MFI-tree树体中相同项的指针链接在一条链表上，链首指针也保存在头表中[12]。

　　在进行超集检测时，不需要对整棵MFI-tree进行投影，先检测待检测项集的第一项在头表中指向MFI-tree的指针是否为空。若为空，则不需要投影，直接添加到MFI-tree中；若不为空，将待检测项集第一项为根节点构建MFI子树。MFI子树构建过程只需要扫描一次MFI-tree中对应结点的后继结点。

　　对于图1中的AFOPT-tree中已挖掘的最大频繁项集{ampfc：3}，MFI-tree如图2所示。有项集{bc：3}，检查其是否在MFI-tree中存在超集。首先检测频繁1-项集b指向MFI-tree的指针为空，故项集在MFI-tree中不存在超集，将项集作为最大频繁项集加入到MFI-tree中，如图2所示虚线分支。再检测项集{bf：3}，因为频繁1-项集b指向MFI-tree的指针不为空，构建以b为根节点的MFI子树，采用基于投影的超集检测该项集在其中不存在超集，将项集作为最大频繁项集加入到MFI-tree中，如图2所示加粗分支。

　　2.2 A-MFI算法

　　与FP-max算法一样，A-MFI算法采用分治递归的策略进行挖掘。在深度优先遍历搜索AFOPT-tree时，通过对遍历到的节点及对应的AFOPT子树头表中的某一项来生成搜索空间的子节点。并在构建AFOPT子树之前先通过优化的基于投影的超集检测来检测首尾项集的并集在已有的最大频繁项集是否存在超集。若存在，则可以进行前瞻剪枝；若不存在，递归的调用算法直到挖掘到某个子孙节点的AFOPT子树为一个单路径树为止，将这个单路径树头表中项集和对应前缀节点的并集作为一个最大频繁项集，加入到MFI-tree中。

　　2.3 算法步骤

　　全局变量：前缀项集p，最大频繁项集树MFI-tree

　　输入：数据量对应的AFOPT-tree，记为T，AFOPT-tree头表中对应的项集h

　　输出：最大频繁项集树MFI-tree

　　A-MFI（T，h）

　　（1）if T是单路径树。

　　（2）将项集p∪h插入MFI-tree中，支持度为单路径树中叶子节点的支持度。

　　（3）else对T头表中的每一项i。

　　（4）将i并入前缀项集p中，为p′。

　　（5）遍历AFOPT-tree获取p′对应的子树头表项集h′。

　　（6）对p′∪h′进行超集检测。

　　（7）if在MFI-tree中不存在超集。

　　（8）创建AFOPT子树T′。

　　（9）A-MFI（T′，h′）。

　　（10）将i从p中移除。

　　3 实验分析

　　为验证算法性能，在内存为DDR3 2 GB、CPU为Core i5-2410M、操作系统为Windows 7 Professional的实验环境下，用VC++ 6.0分别实现了A-MFI算法、FP-max算法和FPMFI算法。实验采用的数据为参考文献[12]中的Mushroom数据库。该数据库中共有8 124条事务记录，平均事务长度为23，一共包含了蘑菇的115种属性。A-MFI与FP-max和FPMFI的运行时间比较如图3所示。

　　从图3的实验结果可以看出，由于A-MFI算法对基于投影的超集检测机制进行了优化，并在存储与数据挖掘相关数据时应用了AFOPT-tree树形结构，在支持度较小时，尤其当支持度小于1%时，相比FPMFI算法和FP-max算法在执行时间上有较大优势。例如在最小支持度为0.1%时，算法FP-max、FPMFI和A-MFI的执行时间分别为15.9 s，8.7 s和6.4 s，算法A-MFI的性能比较同类算法有明显的提升。

　　本文提出了一种基于AFOPT-tree的最大频繁项集挖掘算法，通过对基于投影的超集检测机制进行优化，降低了超集检测的时间消耗；采用AFOPT-tree树形结构存储与数据挖掘相关的信息，提升自顶向下的遍历效率并减少递归次数。实验比较表明，在支持度较小的情况下，本文的A-MFI算法具有明显的优越性。在算法的执行过程中，递归构建AFOPT子树和超集检测消耗了大量的时间和内存，如何进一步地减少递归次数并提高超集检测的效率是以后研究的重点。

　　参考文献

　　[1] AGRAWAL R， IMIELINSKI T， SWAMI A. Mining association rules between sets of items in large databases[C]. Proceedings of ACM SIGMOD International Conference on Management of Data，1993：207-216．

　　[2] BAYARDO R. Efficiently mining long patterns from databases[C]. Proceeding of 1998 ACM S1 GMOD International Conference on Management of Data， New York： ACM Press， 1998：85-93．

　　[3] AGRAWAL R， SRIKANT R. Fast algorithms for mining association， rules[C]. Proceedings of the 20th International Conference on Very Large Database，1994：478-499．

　　[4] GOUDA K， ZAKI M J. Efficiently mining maximal frequent item sets[C]. Proceedings of the IEEE International Conference on Data Mining，2001：163-170．

　　[5] ZHOU QH， WESLEY C， LU BJ. SmartMiner. A depth 1st algorithm guided by tail information for mining maximal frequent item sets[C]. Proceedings of the IEEE International Conference on Data Mining， 2002：570-577.

　　[6] GRAHNE G， ZHU J E． High performance mining of maximal frequent item sets[C]. Proceedings of the 6th SIAM International Workshop on High Performance Data Mining，2003：135-143．

　　[7] GRAHNE G， ZHU J F． High performance mining of maximal frequent item sets[C]. Proceedings of the 6th SIAM Int′I Workshop on High Performance Data Mining，2003：135-143．

　　[8] 颜跃进，李舟军，陈火旺．基于FP-Tree有效挖掘最大频繁项集[J]．软件学报，2005，16（2）：216-219．

　　[9] Liu Guimei， Lu Hongjun， Xu Yabo. Ascending frequency ordered prefix-tree：efficient mining of frequent patterns[C]. Proceedings of the 8th International Conference on Database Systems for Advanced Applications， Kyoto， Japan，2003：65-72.

　　[10] 毛宇星，陈彤兵，施伯乐.一种高效的多层和概化关联规则挖掘方法[J]．软件学报，2011，22（15）：2965-2980.

　　[11] 陈光鹏，杨育彬，高阳，等.一种基于MapReduce的频繁闭项集挖掘算法[J].模式识别与人工智能，2012，25（2）：220-224.

　　[12] 胡德敏，赵瑞可.一种改进的最大频繁项集挖掘算法[J].计算机应用与软件，2012，29（12）：186-188.