摘  要： 提出了一种过滤冗余特征的算法框架，利用组特征选择算法去除冗余特征。在组构造阶段为了弥补单一聚类算法的不足，引入聚类集成的思想，先利用k-means方法通过多次聚类得到一个聚类集体，在集成阶段再利用层次聚类算法对聚类集体进行集成得到最终的结果。实验结果表明，这种算法框架能有效消除冗余特征，在保证算法稳定性的同时还能获得很好的性能。

　　关键词： 稳定性；组特征选择；聚类集成；层次聚类

　　特征选择[1]指从一组特征中挑选出一些最有效的特征以达到降低特征空间维数的目的的过程，是模式识别和机器学习领域中一项必不可少的技术，在数据预处理中发挥重要作用，它广泛应用于文本分类、生物信息学和信息检索等方面。尤其在海量高维数据不断涌现的今天，许多机器学习算法受不相关和冗余特征的影响，而通过选择合适的特征选择算法，可以有效地去除不相关、冗余特征，加速数据挖掘的过程，提高学习算法的泛化性能和运行效率，得到更加简单和容易理解的学习模型[2-3]。

　　围绕提高分类性能和降低特征维数已经提出了很多算法，但是人们往往忽视特征选择的稳定性即特征选择算法的结果对于训练集变化的敏感程度，用于度量训练集的细微变化对最优特征子集的影响[4]。这个问题在很多应用中是很重要的，例如在分析微阵列数据时，由于训练数据的微小变化，同一个特征选择算法可能会选择出差异很大的特征子集，虽然大多数的特征子集在分类性能方面同样优秀[5-6]。这种不稳定性挫伤了领域专家对于生物标志物识别的信心。

　　目前，稳定性问题已成为特征选择的一个研究热点，吸引了众多学者的研究。提高特征选择稳定性的方法主要有3种：（1）借鉴集成学习的思想，利用集成特征选择有效地提高特征选择的稳定性；（2）样本注入的方式；（3）组特征选择[7]。

　　本文将集成方法和组特征选择方法进行结合，提出了一种基于特征聚类集成技术的组特征选择方法，用于提高算法的稳定性。在组构造阶段利用聚类集成的思想对特征进行聚类，弥补单一聚类方法的不足。在组变换阶段，从每个特征组中选出一个特征来代表这个组，最终就得到了最优的特征子集。

　　1 组特征选择

　　相关的特征组通常存在于高维数据中，并且这样的特征组对于训练样本的改变存在抵抗作用[8]。如果把每个特征组看作是一个相关的单独实体，这样既可以去除冗余特征，也可以起到提高特征选择稳定性的效果。现有的组特征选择算法的通用算法框架如图1所示。组特征选择包括组构造和组变换两个关键步骤。

　　1.1 特征组构造

　　组构造是识别相关特征组的过程，特征组的识别包括知识驱动方法和数据驱动方法两类不同的方法。知识驱动方法利用领域知识使得特征组的产生变得容易；而数据驱动方法仅考虑原始的数据，并不考虑领域相关的信息。

　　数据驱动方法利用聚类分析[9]或者密度估计[6]来识别特征簇（组）。在聚类分析方法中通常采用经典的划分算法，例如层次聚类或者k均值等方法来产生特征组。需要注意的是，大多数现有的聚类方法没有明显地考虑特征组的稳定性。

　　数据驱动方法充分地利用了目标数据的特性，因此现在被广泛应用。它的一个最主要的缺点就是不容易解释和验证所选择的特征组。

　　1.2 特征组变换

　　特征组变换即从每个特征组中产生一个单独的相关特征来代表这个特征组。通过从每个组中选择一个代表特征，这样就解决了特征冗余的问题。变换方法从简单的特征值平均[10]到复杂的组成分分析方法[11]等。本文采用的是求中心点的策略。

　　2 特征聚类集成方法

　　假设给定一个训练样本D，它包括n个样本，D={X，Y}={xi，yi}，该数据集中的第i个元素xi为一个d维向量xi=（xi1，xi2，…，xid）∈Rd。

　　聚类集成算法要解决的主要问题有两个，一是如何产生不同的聚类从而形式一个聚类集体，二是如何从这个聚类中得到一个统一的聚类结果，也可称为集成问题。

　　2.1 聚类集体生成

　　在知识驱动方法中采用的聚类分析方法，是无监督特征选择的一个重要方法。但由于聚类分析的不可能性定理[12]，即任何一个聚类算法不可能同时满足尺度不变性、丰富性和一致性，这样就导致没有一个聚类算法可以很好地适用于任何问题。为了解决这个问题，借鉴集成学习[13]的思想，通过组合不同的弱基类模型得到一个性能好的集成模型。因此本文提出一个新的组构造策略，即聚类集成的方法，它可以在不同领域和数据集上有更好的平均性能，能发现任何单个聚类算法无法得到的结合解答[14]。

　　在组构造阶段，使用相同的算法在数据集的不同采样集合上聚类，从而得到多个聚类结果[15]。基于bagging[16]方法，通过可放回抽样获取不同的训练样本子集来训练基聚类器。假设通过bagging方法得到m个不同的训练子集{D1，D2，…，Dm}，单个聚类器采用k-means方法，其中特征之间的相似性度量策略选用相关系数。

　　在m个训练子集上进行多次k-means聚类，得到m个聚类结果，每个聚类结果包括多个特征组，即{F，F，…，F，…，F}，F代表在i次k-means聚类得到的第j个特征组，F代表第m次聚类得到Lm个特征组。

　　2.2 特征聚类集成策略

　　在组构造阶段得到聚类集体后，就需要设计合适的集成方法对多个聚类结果进行集成，这也是聚类集成中的关键问题。本文采用基于互联合矩阵[17]的方法，即在得到的聚类集体{F，F，…，F，…，F}中，计算在所有的特征组F中每对特征被分到一个组的次数，除以集成的次数m，得到每个特征对的相似性Wi，j，再利用凝聚的层次聚类将所有的特征进行聚类得到集成的特征组{EF1，EF2，…，EFL}。为了降低异常值的影响，采用类平均法利用两组特征的相似性来决定是否将它们合并。合并的过程一直持续只要两个特征组的相似性>阈值?兹。?兹是一个用户参数，可以根据不同的数据集进行调整。

　　层次聚类算法需要计算簇与簇之间的距离，目前常用的计算簇间距离的方法有：最短距离法、最长距离法和类平均法。其中类平均法很好地利用所有样本之间的信息，它倾向于合并差异小的两个类，考虑到类的结构，产生的分类具有相对的鲁棒性。

　　本文中提出的算法使用类平均法，两个簇间的距离等于所有分别来自两个簇的点对间的距离的平均值，给定要聚类的对象即d个特征以及d×d的相似行矩阵W，具体的层次聚类方法的步骤如下：

　　（1）将每个特征归为一簇，共得到d簇，每簇仅包含一个特征。簇与簇之间的距离就是两个特征间的相似性。

　　（2）根据相似性矩阵W，若两簇的相似性Wi，j大于阈值?兹，则将这两簇合并成一簇，于是总的簇数少了一个。

　　（3）重新计算新的簇与所有旧簇之间的相似性，计算方法采用类平均法。

　　（4）重复（2）、（3）步，直到类之间的相似性全都小于阈值?兹，则聚类结束。

　　经过以上步骤得到组构造阶段产生的集成特征组{EF1，EF2，…，EFL}，在组变换阶段，需要从每个特征组中产生一个单独的相关特征来代表这个特征组。先对组构造阶段产生的特征组中的所有特征求平均，得到每个组的中心点，再计算组中的所有点到中心点的距离，最后将距离中心点最近的那个点作为特征组的代表特征。这样在组特征选择阶段就得到去除了冗余特征的特征子集{f1，f2，…，fL}。算法的伪代码如下：

　　基于特征聚类集成技术的组特征选择方法

　　输入：数据集D，m个子样本

　　输出：选择出的特征{f1，f2，…，fL}

　　//组构造阶段

　　for i=1，2，…，m

　　从D中可放回抽样得到训练样本Di

　　调用k-means方法得到特征组

　　end for

　　for对每一个特征对xi，xj∈D

　　令Wij=xi和xj分到一组的次数/m

　　end for

　　基于Wij将所有的特征进行层次聚类，得到集成特征组{EF1，EF2，…，EFL}

　　//组变换阶段

　　for i=1，2，…，L

　　从EFi中获取代表特征xi

　　end for

　　3 实验

　　为了验证所提算法的性能，将在不同的基准数据集上进行实验以此来验证算法的稳定性和分类性能。实验所用数据集为：Sonar，Toy，Hill-Valley，Spect Heart，Madelon，Genes均来自UCI数据库[18]，Colon cancer diagnosis数据集来自参考文献[19]。各个数据集的详细信息如表1所示。

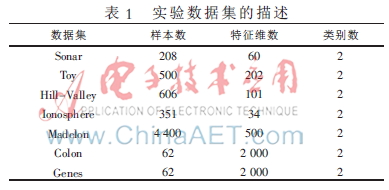
　　实验选取两种集成特征选择方法和一种样本加权方法，用来和本文提出的EFC算法进行对比。它们分别是集成Relief算法（En-relief）、集成fisher score[20]算法（En-fisher score）和样本加权算法VR-Lmba。

　　3.1 稳定性实验

　　为了验证本文所提算法的稳定性，采取基于bagging方法的可放回抽样。首先，对于非集成方法VR-Lmba，对原始数据集进行10次可放回抽样，每次随机抽取90%（观察样本的微小变化）的样本构成新的训练样本子集，计算VR-Lmba算法的平均稳定性；其次，计算En-relief、En-fisher score两个集成算法的稳定性，利用集成思想在训练子集上进行二次抽样，采样比例为90%，在得到的样本子集上进行集成特征选择，得到m个不同的特征权重向量。再利用线性加权集成方法，获取每个训练子集的集成结果，最后计算特征子集间的平均稳定性；对于EFC算法，与上述集成方法的实验方法相同，不同的是EFC算法的输出是10个特征子集，无需线性集成的过程。其中，计算一对特征子集稳定性的方法是杰卡德系数[21]，最终的稳定性是所有不同特征子集对的平均稳定性。算法的稳定性对比实验结果如图2所示。X轴代表基特征选择器的个数m。VR-Lmba算法不是集成算法，因此它的稳定性不会随m值变化。

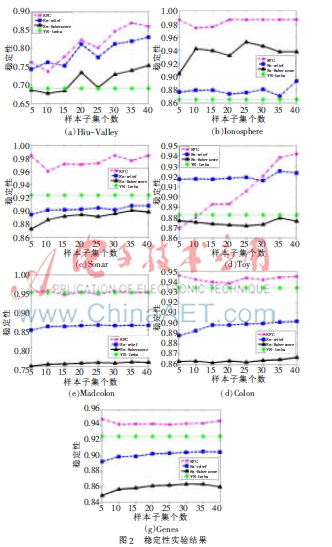
　　通过以上稳定性的对比实验，可以观察到EFC算法的稳定性与其他算法相比有相似或者高于它们的稳定性。而且随着基特征选择器数目的增加，稳定性也随之提高，当基特征选择器到达一定数目后，稳定性基本保持不变。

　　3.2 分类准确率实验

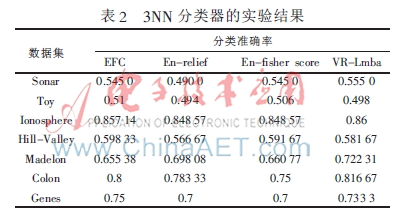
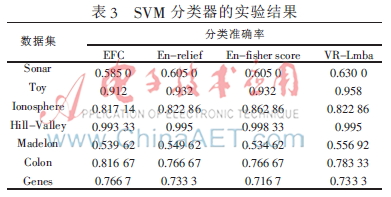
　　由于不存在普遍接受的聚类性能的评价指标，本文将利用分类准确率来验证所提算法的性能。实验采用10次交叉验证，分类器选取k（k=3）近邻分类器和线性SVM（C=1）分类器，集成特征选择基分类器的个数m=20。4种算法的分类准确率实验结果如表2和表3所示，分别对应3NN和SVM分类器。

　　本文提出了一种过滤冗余特征的算法框架，利用组特征选择算法去除冗余特征，在组构造阶段引入聚类集成的思想，集成方法采用基于互联合矩阵的方法，利用基于相似性的层次聚类算法对聚类集体进行集成。

　　实验结果表明所提算法能有效消除冗余特征，保证算法稳定性的同时还能获得很好的性能，能有效地处理高维和噪声数据。算法的不足之处就是集成阶段，由于层次聚类中使用距离矩阵，所以它的时间和空间复杂性都是二次以上的，这也是未来对本论文所提算法的一个改进方向。

　　参考文献

　　[1] 张学工.模式识别（第三版）[M].北京：清华大学出版社，2010.

　　[2] DASH M， LIU H. Feature selection for classification[J]. Intelligent data analysis， 1997， 1（1-4）：131-156.

　　[3] KOHAVI R， JOHN G H. Wrappers for feature subset selection[J]. Artificial intelligence，1997，97（1）：273-324.

　　[4] K P， K J， H V. Improving stability of feature selection methods[C]. Proceedings of the 12th International Conference on Computer Analysis of Images and Patterns， 2007：929-936.

　　[5] KALOUSIS A， PRADOS J， HILARIO M. Stability of feature selection algorithms： a study on high-dimensional spaces[J]. Knowledge and Information Systems， 2007（12）：95-116.

　　[6] YU L， DING C， LOSCALZO S. Stable feature selection via dense feature groups[J]. Proceedings of the 14th ACM International Conference on Knowledge Discovery and Data Mining， 2008：803-811.

　　[7] AWADA W， KHOSHGOFTAAR T M， DITTMAN D， et al. A review of the stability of feature selection techniques for bioinformatics data[C]. 2012 IEEE 13th International Conference on， Information Reuse and Integration， IEEE， 2012： 356-363.

　　[8] LOSCALZO S， YU L， DING C. Consensus group stable feature selection[C]. Proceedings of the 15th ACM SIGKDD international conference on Knowledge discovery and data mining， 2009： 567-576.

　　[9] AU W H， CHAN K C C， WONG A K C， et al. Attribute clustering for grouping， selection， and classification of gene expression data[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics （TCBB）， 2005， 2（2）： 83-101.

　　[10] GUO Z， ZHANG T， LI X， et al. Towards precise classification of cancers based on robust gene functional expression profiles[J]. BMC Bioinformatics，2005，6（1）：58.

　　[11] RAPAPORT F， ZINOVYEV A， DUTREIX M， et al. Classification of microarray data using gene networks[J]. BMC Bioinformatics， 2007，8（1）：35.

　　[12] KLEINBERGJ. An impossibility theorem for clustering[C]. Advances in Neural Information Processing Systems， 2002：446-453.

　　[13] DIETTERICH T G. Ensemble methods in machine learning[C]. Proceedings of the 1st International Workshop on Multiple Classifier Systems， Cagliari， Italy， 2000：1-15.

　　[14] 罗会兰.聚类集成关键技术研究[D].浙江：浙江大学，2007.

　　[15] STREHL A， GHOSH J. Cluster ensembles-a knowledge reuse framework for combining multiple partitions[J]. Journal of Machine Learning Research， 2002（3）：583-617.

　　[16] GAO J， FAN W， HAN J. On the power of ensemble： Supervised and unsupervised methods reconciled[C]. Tutorial on SIAM Data Mining Conference （SDM），2010.

　　[17] FRED ALN. Finding consistent clusters in data partitions[C]. Multiple Classifier Systems，2001：309-318.

　　[18] FRANK A， ASUNCION A. UCI machine learning repository[DB]. http：//archive.ics.uci.edu/ml.2010.

　　[19] ALON U， BARKAI N， NOTTERMAN D A， et al. Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon cancer tissues probed by oligonucleotide arrays[J]. Proceedings of the National Academy of Sciences of the United States of America， 1999： 6745-6750.

　　[20] TSUDA K， KAWANABE M， MＯ?譈LLER K R. Clustering with the fisher score[J]. Advances in Neural Information Processing Systems， 2002（15）：729-736.

　　[21] HE Z Y， YU W C. Stable feature selection for biomarker discovery[J]. Computational Biology and Chemistry， 2010,

　　34（4）:215-225.