摘要： 在分析人脸结构特征的基础上，通过引入人脸主要器官的结构约束并结合改进的方向梯度直方图特征和增量SVM， 提出了一种新的人脸跟踪算法。实验证明，该算法能够显著提高人脸跟踪过程的稳定性和准确性，并具有良好的实时性能。

　　关键词： 人脸跟踪；结构信息；方向梯度直方图；增量SVM

　　目标跟踪是人工智能领域中最重要的核心问题之一，在工农业、娱乐及军事领域都具有非常重要的应用价值[1]。目前，在目标跟踪研究中，常用的方法主要分为基于模型的方法和模型无关的方法两大类。基于模型的方法需要事先对拟跟踪的目标进行详细的研究，手工标注大量的样本并建立目标模型实现对目标的跟踪。这类方法前期工作量大，跟踪过程的实时性差，而且难以适应随机变形的目标，特别是当目标较复杂，难以获得精确的模型时，这类方法将完全失效。与模型无关的方法一般通过自动提取目标特征和相似度比对实现目标跟踪过程。该类方法不需要事先知道目标的先验信息，可以在跟踪过程中不断对目标特征进行学习，来改善和丰富对目标的理解。模型无关的方法能够快速建立目标跟踪并在线学习以适应目标变化的特点,使其具有更好的应用价值，是目前研究的热点[2]。

　　人脸跟踪是当前目标跟踪领域研究的一个热点，其在治安、娱乐、科研等领域具有很大的现实意义。人脸目标介于刚体和柔性体之间，具有以下特点：人脸大致轮廓和内部器官之间结构关系相对稳定；跟踪过程中内部结构之间的空间位置存在变形，但满足一定约束；内部结构本身的形状和大小也可能存在变形。本文通过研究人脸目标的结构及外观特点，提出了一种新的结合结构约束的人脸跟踪方法，其基本思想是，为人脸主要的器官(双眼、嘴)建立独立的描述和比较模块，并对器官间的结构约束进行建模，利用结构信息辅助完成目标搜索和评分，最终确定目标位置。实验证明，该方法进行人脸跟踪的准确度和稳定性较传统CamShift等算法有明显提高，而且具有良好的实时性，具有较高的应用价值。

　　1 方法

　　1.1人脸结构约束

　　人脸具有典型的结构化特征，通常所谓的“五官”按照规则排列在人脸上，这些器官之间存在明显的结构约束，但又可以进行较大程度的变形[3-4]。在人脸跟踪过程中,利用人脸各部分分别建模可以增加特征的稳定性，提高跟踪的精度[4]；同时，引入各结构之间的约束关系，能够提高人脸跟踪的适应性，排除误报。在人脸图像中，五官中的双眼、嘴往往具有较大的显著性，而鼻子、耳朵特征一般较为模糊，特别是在光线、角度不理想的情况下，鼻子、耳朵常不能提供有效的特征。因此，本文以双眼、嘴共3个面部主要器官为对象，对它们的空间结构约束进行建模。定义评价函数：

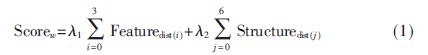
　　其中,Scorew为对于窗口图像w的评分。等式右边包括两部分，第一部分为检测图像与目标的特征相似度，本文通过方向梯度直方图结合SVM获得；第二部分为目标各模块之间的结构化约束评分。为了兼顾跟踪的准确性和实时性要求，这里结构信息采用了双眼间向量(距离，角度)、嘴部与双眼间向量(距离，角度)共6个约束形成的三角形作为结构约束，如图1所示。?姿1、?姿2分别是两部分的权重因子。人脸跟踪的过程就是寻找式(1)最小值的过程。

　　1.2 改进的方向梯度直方图

　　方向梯度直方图HOG(Histogram of Oriented Gradient)特征是一种常用的图像特征描述子，如图2所示，由法国国家计算机技术和控制研究所的DALAL N和TRIGGS B在2005年的CVPR上首次提出。由于其对几何和光学变形具有良好的适应性，HOG特征已经被广泛应用于计算机视觉和图像处理中[5]。通过计算和统计图像局部区域的HOG来构成特征。为了对各模块进行特征提取并保证系统的实时性，本文根据人脸跟踪的具体情况对经典HOG算法进行了针对性的优化，方法如下。

　　(1)对输入图像进行颜色空间的标准化(Gamma校正法)，以降低图像局部的阴影和光照变化所造成的影响。

　　(2)获取滑动窗图像并灰度化，将图像统一为48×64大小的标准图像。

　　(3)计算图像每个像素的方向梯度。

　　(4)根据跟踪的目标大小,将图像划分成4像素×4像素的方格。

　　(5)将360°按每个方向45°划分为8个方向。与经典HOG算法不同，本文根据每个像素的梯度方向，将其幅值线性差值计入与其方向相邻的两个方向通道内，统计每个方格的HOG。

　　(6)将所有方格得到的HOG串联起来便得到改进的HOG特征。

　　与经典算法相比，优化的HOG特征简化了图像分块策略，提高了特征计算的速度。同时，由于增加了方向差值过程，使方向梯度的稳定性得到了较大提高，具有更好的抗噪声性能。实验证明，在本应用中该特征在提高计算速度的前提下对图像具有不低于经典HOG算法的表征能力。

　　1.3 增量SVM

　　支持向量机(SVM) 是VAPNIK等人提出的一种经典的机器学习方法，由于其优越的学习能力，一经提出就在国内外学术界受到广泛重视。SVM算法通过使用非线性映射将低维样本映射到高维空间，并在高维空间使用结构风险最小化理论构建全局最优分割超平面，能够使整个样本空间的期望风险以某个概率满足一定上界[6]。

　　虽然SVM具有很多优势，但其经典理论并不具有增量学习的能力，即要求使用者在训练初期能够收集一个相对完整的训练集[7]。对于非模型目标跟踪来说，在跟踪初期，对目标的描述和理解往往是片面的，很难获得完善的训练集，因此需要在跟踪过程中对学习机进行不断的修正。如果使用经典SVM训练方法，每次增加样本时，需要对所有原始样本重新训练，训练时间将随着跟踪的持续而不断提升，最终导致不能实时跟踪。为了解决这一问题，本文将核函数局部化算法引入SVM理论，实现在不显著增加训练时间的前提下不断更新样本，使SVM分类精度可以随着跟踪的进行和样本集的积累而逐步提高。需要特别指出的是，本文在式(1)中使用的是SVM的特征距离，而非SVM预测标签。

　　首先按照经典SVM训练方法得到初始分类器，经典SVM的判别函数一般表示为：

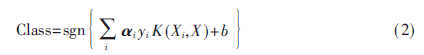
　　其中，K(·)为核函数，获得最优超平面f和支持向量集SV。利用核函数的局部特征，当跟踪到目标得到新的样本后，验证KKT条件:

　　其中，非零?琢i为支持向量。判断新样本是否能被超平面f正确分类，如果新样本能够被正确分类，则说明该新样本在分类内部，此时不需要对分类器进行修正，即可进行下一轮跟踪；如果不能被正确分类，则需要调整分类器。需要指出的是，当新增样本违背KKT条件时，原样本集中非支持向量也可能转化为支持向量，因此需要由新增样本得到一个新的SVM来检验原始样本是否违背KKT 条件。最终由所有支持向量与所有违背KKT条件的样本组合构成新的训练集，并得到最终的新的SVM。该增量学习方法不仅具有良好的数学基础，而且仅使用现有样本中少量的样本进行重新训练，大大降低了SVM的训练时间，提高了系统实时性[6]。

　　2 结合结构信息的人脸跟踪算法

　　综合以上各部分，本文提出的算法具体流程如下：

　　(1)获取第一帧图像并手动框定人脸及双眼、嘴部区域，生成初始化样本集。

　　(2)提取双眼、嘴部改进的方向梯度直方图特征，训练初始SVM；计算结构约束，初始化结构参数。

　　(3)取下一帧，搜索双眼及嘴部候选区域，记录SVM距离。

　　(4)在候选区域中寻找最小化式(1)的区域，作为跟踪结果。

　　(5)根据跟踪结果修正结构参数。

　　(6)每累计跟踪10帧，利用新的正负样本(正样本为跟踪到的目标，负样本为搜索过程中获得的目标周围的图像区域)增量更新SVM。

　　(7)返回到步骤(3)，进行下一轮跟踪。

　　3 实验

　　实验所用的计算机平台为I3-2120 @3.30 GHz CPU，4 GB内存，操作系统为Windows XP SP3。测试程序在MATLAB 2011b平台下实现。本文选取了近年来比较著名的电影和电视剧中的片段作为测试对象。在这些片段第1帧用鼠标框取了待跟踪人脸及其双眼和嘴部，从第2帧开始进行跟踪，部分结果如图3所示。将本文提出的算法与经典CamShift算法相比较，结果如表1所示,可以看出本文算法在跟踪精度上具有明显优势。

　　本文通过研究人脸的结构特征，对人脸主要器官的结构约束进行建模，并结合改进的HOG与增量SVM,开发出一种新的人脸跟踪算法。实验结果表明，本文提出的算法能够在人脸跟踪过程中更好地适应目标的角度变化和部分遮挡，跟踪精度和稳定性优于传统的CamShift算法，并能够达到实时性要求。

　　参考文献

　　[1] 马晓路，刘倩，牟海军.基于Mean Shift 和粒子滤波的运动目标跟踪[J].微型机与应用,2012，31(23)：42-44.

　　[2] 张宝峰，赵建平，朱均超. 基于OpenCV的室内环境下多目标跟踪[J].微型机与应用, 2013，32(9)：24-26．

　　[3] Zhang Lu， Laurens van der Maaten． Structure PreservingObject Tracking[C]． 2013 IEEE Conference on Computer Vision and Pattern Recognition，2013:1838-1845．

　　[4] BRANSON S, PERONA P, BELONGIE S. Strong superv-ision from weak annotation: interactive training of defor-mable part models[C]. 2011 IEEE International Conference on Computer Vision, 2011:1832-1839.

　　[5] 王文武， 王华昌. 嵌入式客流量统计模块的设计和实现[J].电子技术应用,2011，37(8):33-35.

　　[6] 牛胜石，毛晓晖，侯建华，等.基于Adaboost和SVM的人头实时检测[J].微型机与应用,2010，13(1)：33-36.

　　[7] 潘以桢， 胡越明. 改进的在线支持向量机训练算法[J].计算机工程,2009，35(22)：212-215.