0 引言

    MIMO技术充分利用了空间资源，可以通过空间复用、空间分集或智能天线技术达到提高数据比特率、降低误码率或提高信噪比的目的^[1]，但当系统中天线之间具有空间相关性时，会对系统性能造成影响。参考文献[2]研究了拉普拉斯角能量分布条件下均匀圆阵下的空间相关性，分析了衰落因子和归一化间距对空间相关性的影响。参考文献[3]与参考文献[4]分析了均匀线阵与均匀圆阵下空间相关性对系统误码性能的影响；参考文献[5]研究了空间相关性对信道容量的影响，在这些研究中均未将收发结合进行研究。本文首先研究MIMO系统的空间相关性模型，然后根据该模型，针对上述研究中的不足，研究均匀线阵和均匀圆阵结合的2发4收MIMO系统空间相关性对误码性能和信道容量的影响。在本文分析中，未考虑信号的传输距离的衰落和多普勒的影响。

1 MIMO空间相关性模型

    MIMO天线空间相关性主要指发射端与接收端天线之间的相关特性，用相关系数进行表征。假设任意两个接收天线的相关性与发射天线是哪一个无关，两个发射天线之间的相关性与接收天线是哪一个也没有关系^[6-7]。

    对第m个天线阵元和第n个的天线阵元的相关系数定义为^[2]：

其中，λ为无线电波波长，M表示天线个数，d是线阵天线间距，θ是发射信号的离开角或接收信号的到达角，φ为发射信号或接收信号的俯仰角(本文中假定为φ=90°)，R为均匀圆阵的半径，Ψ表示圆阵的位置方位角。

    常用的角能量谱概率分布包括高斯分布、均匀分布和拉普拉斯分布，在城区和农村环境下，拉普拉斯角能量分布是与信道测量结果吻合最好的一种分布^[9]。因此本文研究拉普拉斯角能量分布情况下的MIMO天线的空间相关性。

    拉普拉斯角能量分布方程^[8]为：

    可以认为角分布标准差σ即为角度扩展，随着角度扩展的增大，衰落因子相应减少，反之亦然。

    将式(2)、(3)、(4)代入式(1)，可得均匀线阵和均匀圆阵下的空间相关性系数^[3-4]。

2 空间相关性对误码率的影响

    参考文献[8]对均匀线阵和均匀圆阵情况下，采用最大比合并，假设是准静态信道，不考虑多普勒的影响，得出了空间相关性与误码率的关系，如式（10）所示：

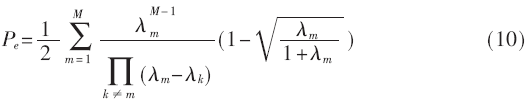
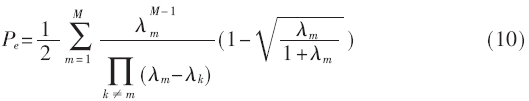
式中，λ_m为空间相关矩阵R_h的特征值，R_h=γ_cR_v，γ_c是接收到的每天线每比特的信噪比，式(10)是采用BPSK调制解调下的性能特性，也可适用于采用格雷编码的QPSK。由式(10)，需要计算MIMO信道的整体相关矩阵R_v，从而计算特征值，R_v可以通过下式进行计算[6]：

3 空间相关性对信道容量的影响

    当得到系统的发射相关矩阵和接收相关矩阵后，可以根据式(12)计算MIMO系统的信道传输矩阵H^[7]：

其中，H_iid为随机矩阵，其元素为独立同分布的零均值复高斯变量，(·)^1/2表示矩阵的平方根分解。当发射端不知道信道状态信息时，采用等功率发射，即每根天线上分配相同的功率，MIMO信道的瞬时容量为[5]：

其中，(·)^H表示矩阵的复共轭转置，I表示单位矩阵，ρ是平均信噪比，n为发射天线数和接收天线数的最小值。由式(13)，信道容量与MIMO的信道传输矩阵有关，而信道传输矩阵又受发射与接收天线的空间相关性影响，将在下节中通过计算分析空间相关性对信道容量的影响情况。

4 计算与分析

4.1 空间相关性分析

    根据式（6）、（7）、（8）、（9）分别计算均匀线阵和均匀圆阵的空间相关值并取模，得到均匀线阵和均匀圆阵的相关值曲线分别如图1、图2所示，图1是线阵阵元1和阵元2的相关性，圆阵的阵元分别位于圆周的π/4、3π/4、5π/4和7π/4处。

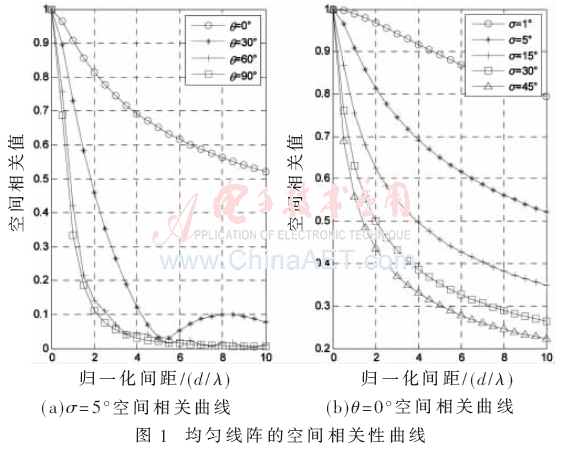
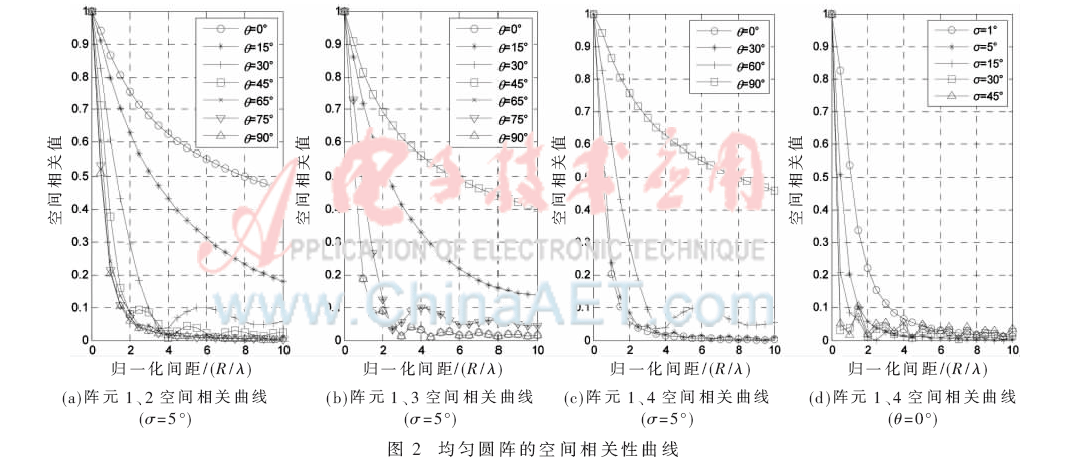
    由图1和图2可以看到，当σ确定时，空间相关值总体趋势是随着归一化间距的增大而相应减小，因此可以通过提高无线电波频率或增大天线之间距离的方法来增大归一化间距以减少空间相关性，但这种减少趋势受θ的影响，会出现一些波动。而θ对空间相关性则有不同的影响，跟天线阵元的结构、位置有关，如对于均匀圆阵，由图2，阵元1、2之间的空间相关性随θ的增大而减小，阵元1、4之间的空间相关性则随着θ的增大相应增大，但阵元1、3之间空间相关性则不是单调关系，θ为45°时空间相关性最大，其余则是关于θ=45°对称变化。

4.2 误码性能分析

    图3是根据式(10)计算的空间相关性与误码率之间的关系曲线，均假设发射端采用2阵元的均匀线阵，接收端采用4阵元的均匀圆阵，发射端的归一化间距均为2，平均到达角或离开角均为5°。

    图3(a)中，信噪比一定，改变角度扩展和归一化间距，随着角度扩展或归一化间距的增加，误码率降低；但当角度扩展或归一化间距增加到一定程度后，对误码改善的能力趋于平缓。相较而言角度扩展对误码性能的影响更大。图3(b)中，接收端归一化间距为4，改变角度扩展和信噪比，随着信噪比的增加，误码率降低，当信噪比一定时，与图3(a)相同；随着角度扩展的增加，误码性能虽得到改善，但这种改善随着角度扩展的增大逐渐减小。

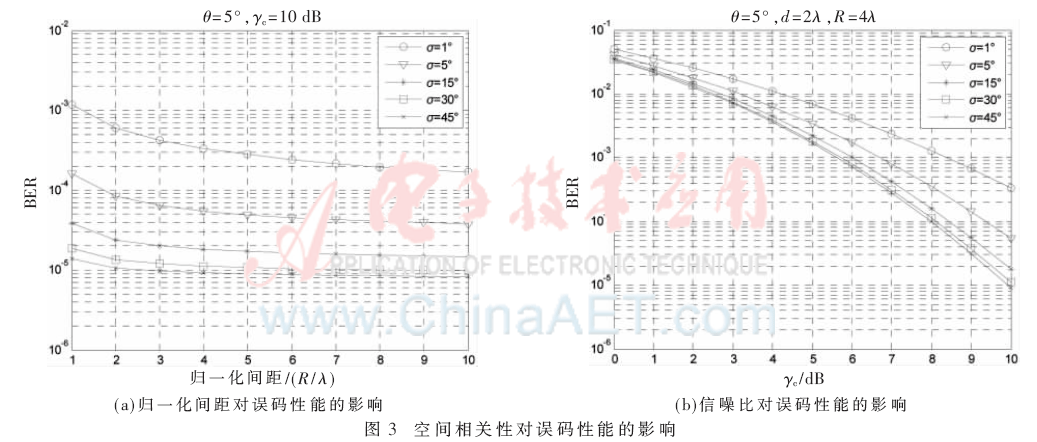
    由图3可以看出，当阵元之间的归一化间距或角度扩展增大时，由3.1节的分析，都会减少天线之间的空间相关性，使得误码性能得到了改善，但这种改善随着归一化间距的增大或角度扩展的增加而趋于减小。

4.3 信道容量分析

    空间相关性对信道容量的影响如图4所示。发射端采用2阵元均匀线阵，归一化间距为2，接收端采用4阵元均匀圆阵，图4(a)中，接收端归一化间距为4，当信噪比增加时，瞬时信道容量相应增加，而当信噪比确定时，随着角度扩展的增大，空间相关性减小，瞬时信道容量相应增加。图4(b)中，当归一化间距逐渐增大时，信道容量出现一定波动，这种波动随着间距的增大和角度扩展的增大而减小，特别是当角度扩展较大时，波动已经很小，说明角度扩展对信道容量的影响较归一化间距的影响更为显著。

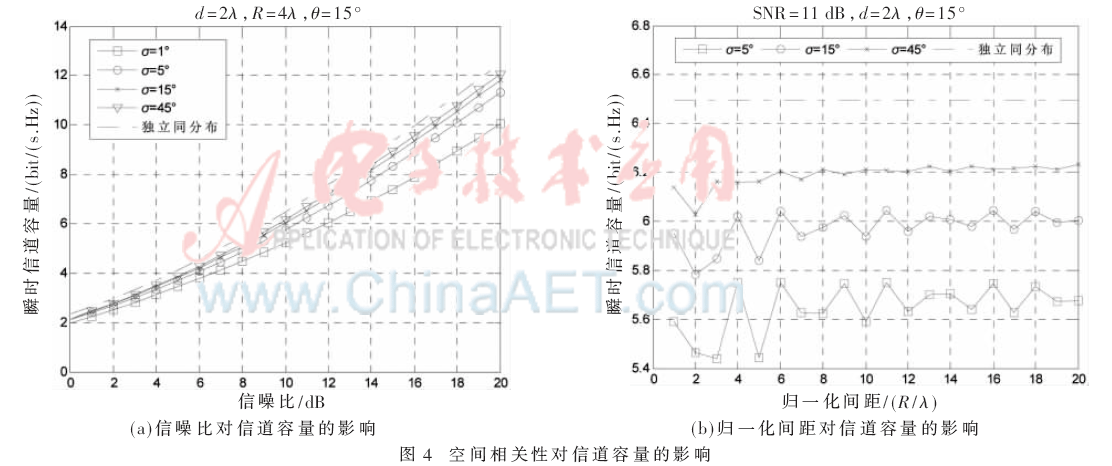
5 结论

    本文在拉普拉斯角能量分布条件下，以均匀线阵和均匀圆阵为例，分析了MIMO系统的空间相关性模型、空间相关性对误码率及信道容量的影响。而天线阵元间的空间相关性主要取决于发射端和接收端天线的拓扑结构、天线间距、发射信号的离开角与角度扩展、接收信号的到达角与角度扩展以及角度功率谱等空间参数。在这些影响因素中，发射信号的离开角或接收信号的到达角对空间相关性的影响跟阵元拓扑结构相关，而归一化间距和角度扩展的增加均会减小空间相关性，相较而言，角度扩展比归一化间距对系统的误码率和信道容量的影响更大，这是在设计MIMO系统时均要考虑的因素。

参考文献

[1] 刘晓明，何徽，吴皓威，等.ADS5287及其在MIMO接收机中的应用[J].电子技术应用，2011，37(10)：52-55.

[2] TSAI Jiann-An，BUEHRER R M.Spatial fading correlation function of circular antenna arrays with laplacian energy distribution[J].IEEE Communications Letters，2002，6(5)：178-180.

[3] TSAI Jiann-An，BUEHRER R M，WOERNER B D.BER performance of a uniform circular array versus a uniform linear array in a mobile radio environment[J].IEEE transactions on wireless communications，2004，3(3)：695-700.

[4] 钱崟，周杰.天线相关性对MIMO系统BER性能的影响分析[J].电信科学，2012(5)：51-59.

[5] SHIU Da-shan，FOSCHINNI G J，GANS M J，et al.Fading correlation and its effect on the capacity of multielement antenna systems[J].IEEE Transactions on Communications，2000，48(3)：502-513.

[6] 黄丘林.MIMO无线通信技术研究[D].西安：西安电子科技大学，2007.

[7] 徐晓军.MIMO无线信道建模与仿真[D].成都：电子科技大学，2006.

[8] 黄超.MIMO系统空时相关性与天线阵列[D].南京：南京信息工程大学，2007.

[9] PEDERSON K I，MOGENSEN P E，FLEURY B H.Spatial channel characteristics in outdoor environments and their impact on BS antenna system performance[J].Proceedings of IEEE VTC 1998，2：719-723.