摘 要: 将神经元自适应的控制模型与常规PID控制算法相结合,设计了一种自适应PID控制器,并将其应用于风力发电机试验系统电源组的控制系统中。该控制器不仅结构简单、参数易于整定,且具有较好的自适应和自学习功能。结果表明,应用神经元PID控制的风力发电机试验系统的电源组控制系统能够适应被控对象在较大范围内的变化,具有较强的自适应性和优良的控制性能。
关键词: 试验系统;风力发电机;神经元自适应控制;PID控制
目前风力发电试验系统所使用的电源控制系统,其调节对象具有时变性、多样性、不确定性和非线性等特点,因此针对该试验电源组控制系统难以建立精确的数学模型,而且试验电源组控制系统的动态特性及运行参数依赖于它的运行环境与运行工况。由于其控制参数是在一定条件(如环境、工况等)下设定的,当条件发生变化时,原整定参数不再适应于当前对象的动态特性,以至于使控制品质下降。而常规的PID控制的参数是根据调节对象的数学模型来进行整定的,所以对于风力发电试验系统电源组控制采用常规的PID控制器难以取得理想控制效果[1]。为了克服常规PID 控制存在的缺点,将神经元自适应PID控制器引入风力发电试验系统电源组控制中。
本文是基于湖南省科技计划项目——风力发电机智能综合测控系统的研究,根据试验过程要求自动实现试验电源组各单元的控制,将神经元自适应PID控制用于电源组控制系统,以实现理想的控制效果。将神经元PID控制器的工程应用与仿真研究相结合,在实现神经元PID控制的优良性能的基础之上,探索神经元自适应PID控制器参数的工程整定方法。
1 风力发电机试验系统电源组控制系统

图1所示为风力发电机试验系统电源组的控制系统结构框图,系统是由神经元自适应PID控制器、调节器、触发器、执行机构、滤波、辨识环节、检测电路、负载构成的一个闭环控制回路。
将给定信号(电压、电流)的输入值与负载电压、电流检测反馈值进行比较,为了消除给定输入值与反馈值的误差,将误差送入神经元自适应控制器,由调节器产生的控制信号根据一定的算法来进行调整,发出电压、电流信号给执行机构,以实现电压(转速)及电流闭环控制,无差调节。在电源组内部设置一个辨识环节,能有效辨识给定与输出信号,从而实现输出电流和输出电压(转速)的稳定[2]。因此,由外部电网和负载波动等引起的电流变化,均可通过快速调节输出电压而保持输出电流的稳定以及良好的调节性能。充分利用神经元自适应PID控制的自学习和自适应能力来克服负载的波动,从而实现电源组稳定、可靠地长期运行。
2 神经元自适应PID控制器设计
2.1 神经元自适应PID控制器的基本原理
在神经网络控制中,单神经元是最基本的控制单元。神经元PID 控制器具有现场整定参数简单、便于现场调试的重要特点, 能够大大改善典型非线性时变对象的动态性能, 能够适应过程的时变特性, 以保证控制系统在最佳状态下运行[3]。
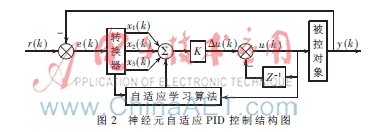
神经元自适应PID控制的结构如图2所示。图中转换器的输入反映被控过程及控制设定的状态。设r(k)为设定值,y(k)为输出值,误差e(k)经转换器转换后成为神经元的输入量x1(k)、x2(k)、x3(k)。利用神经元的在线调整功能,把神经网络应用于PID控制系统中,以改善常规PID的控制性能[4-5]。
其增量式表示为:

由式(1)、(2)、(3)可知神经元控制器输出的x1(k)、x2(k)、x3(k)即为PID调节器的比例、积分、微分输入,而w1、w2、w3即为对应的加权系数[6-7]。神经元自适应PID控制器通过某种学习算法不断更新修改加权系数,从而实现自动适应被控对象的状态环境变化的自学习、自适应功能,所以神经元PID控制器也可称为在线自适应PID控制器。
2.2 自适应控制规律
(1)一般神经元PID控制规律
本文采用的一般神经元自适应PID控制的控制规律为:
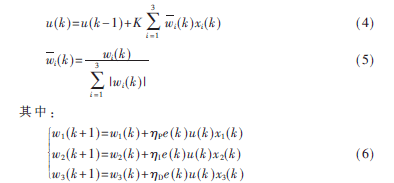
式(6)中,K为神经元比例系数,?浊P、?浊I、?浊D为比例、积分、微分的学习效率。对比例(P)、积分(I)、微分(D)分别采用不同的学习效率?浊P、?浊I、?浊D,以便对它们各自的权系数能根据需要分别进行调整。学习效率的取值可先由现场实验或仿真来确定。
(2)改进的神经元自适应PID控制规律
神经元PID参数的在线学习修正主要与 e(k)、?驻e(k)及神经元比例系数K有关,因此可将神经元自适应PID控制算法中的加权系数学习修正部分及比例系数K进行修改,即将其中式(4)中的xi(k)改为e(k)+?驻e(k),由式(4)可知神经元的比例系数K为一常数,为了抑制较大扰动量的影响(负载的突加与突卸时),将K设定为一个随e(k)和?驻e(k)变化的变量,当误差较大时K值也较大,当误差较小且接近稳定时K值较小,这时K值对系统的稳定性影响较小。对上述控制规律稍加修改后的算法如下:
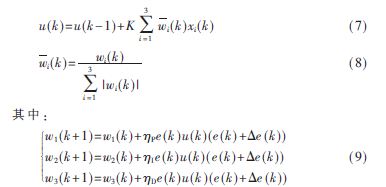
采用上述改进的控制规律,权系数的在线修正就不完全是根据神经网络学习原理,而是参考现场实际经验来制定的。比例系数K不再是一个恒定值,而是一个随误差变化的变量,有利于提高系统的稳定性。
3 仿真分析
对于风力发电机试验系统电源组的控制系统,其负载的种类很多,有的结构和工作过程相当复杂,其内部不止一个状态变量,要准确描述其数学模型比较困难,且阶次很高。但是在实际分析问题时,没有必要用到特别复杂的高阶次的数学模型,而且通过仿真说明采用低阶次的近似简单数学模型不仅实用,且能得到比较满意的仿真结果。因此本文选取的负载被控对象为二阶系统
在对常规PID仿真中,取常规PID参数为:Kp=0.10,Ki=0.01,Kd=0.10,采样时间Ts=1 ms。在对一般神经元自适应PID仿真中,取学习效率?浊p=0.40,?浊i=0.35,?浊d=0.40,K=0.052,采样时间Ts同为1 ms。采用一般神经元自适应PID控制与常规PID控制算法仿真对比结果如图3所示,误差跟踪曲线对比如图4所示。

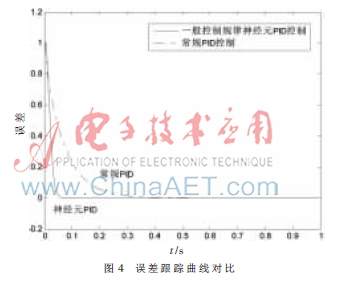
由图3、图4可知,神经元自适应PID控制器的控制性能要优于常规PID控制器,能够对参数在线自适应调整以实现良好的控制效果,较常规PID控制器的快速性、稳定性好,且没有超调,可以达到理想的控制效果。而采用改进控制规律的神经元自适应PID控制根据实际情况,取a=0.12、?琢=0.2、?茁=0.3,其余参数保持不变,其与常规PID控制算法仿真对比结果如图5所示,图6所示为其误差曲线比较。

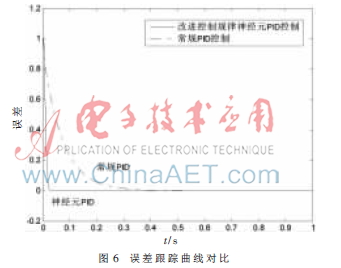
由图5、图6可以看出,改进控制规律的神经元自适应PID控制要优于一般的神经元PID控制,其快速性更好,可以使系统更快地趋于稳定,减少了系统的误差,具有良好的控制性能。在不同情况下,试验系统的电源组需要带不同的负载,其传递机构的传递函数或者负载主电路发生变化时,只要改变增益K的初始值以及对应于误差的权值?琢、?茁就可以获得理想的效果,较一般的神经元PID控制器与常规PID控制器调节起来更加方便实用。
仿真结果表明:常规PID控制效果虽然具有调节方便、结构简单等优点,但是其控制难以达到理想的效果,尤其是当对象为非线性时,通常会出现调节时间过长的弱点;而神经元自适应PID控制具有优于常规PID控制的控制效果。
本文提出的神经元自适应PID控制器具有结构简单、控制算法简单易懂、实现方便等特点,既保持了常规PID控制的优点,又有很强的自学习智能特性,将其应用于风力发电机试验系统电源组的控制系统中,以其良好的自适应性,可以自学习地对PID参数进行实时调整。试验过程实现了对系统各单元的自动控制,达到了节能最佳的目的,电源的波形及各项指标符合国家标准,达到了理想的控制效果。
参考文献
[1] 李作军.基于DSP的变频电源数字化控制技术的研究[D].武汉:武汉理工大学,2008.
[2] 李小英,匡宇国.模糊自适应整定PID-FS在整流电源中的应用[J].电力电子技术,2007,41(2):63-65.
[3] LIN W M,HONG C M.Fuzzy neural network output maximization control for sensorless wind energy conversion system[J].Energy,2010,35(2):592-601.
[4] 王迎旭,沈学军.神经元自适应PID控制器在机组控制中的应用[J].控制工程,2004,11(2):206-208.
[5] 张学燕.神经网络自适应PID控制器的研究与仿真[D].贵阳:贵州大学,2008.
[6] 刘金琨.先进PID控制MATLAB仿真[M].北京:电子工业出版社,2004.
[7] 王迎旭,刘国繁,伍萍辉.基于神经网络的自适应PID控制器及其应用[J].电力电子技术,2004,38(2):89-91.

