摘 要: 无线传感器网络通过少数确定锚节点计算到其他节点距离,确定节点坐标。其中DV-Hop定位算法通过最小二乘法求解坐标,累计误差随节点平均距离误差呈指数增长,定位精度较低。提出了用粒子群PSO离散算法替代DV-Hop中的最小二乘法, 既发挥PSO全局搜索能力,又避免标准PSO算法过早收敛的问题。实验结果表明,新算法定位精度很高,受距离误差影响不大,能很好地应用于无线传感器网络的定位过程。
关键词: 无线传感器网络;粒子群;DV-Hop定位算法;离散算法
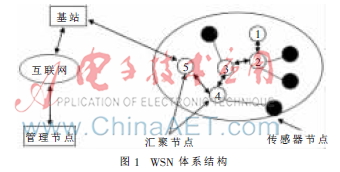
无线传感器网络WSN(Wireless Sensor Networks)由大量传感节点以多跳自组织方式构成,通过数据采集、协调感知完成信息搜集和管理任务。无线传感器网络一般应用于恶劣环境或是人无法抵达区域,受铺设成本和能源供给限制,只有少数汇聚节点配备GPS定位装置,通过与网络其他传感器节点接力通信完成对其定位过程。典型的WSN由传感器节点、汇聚节点和管理节点组成,如图1所示。传感器节点感知目标信息后以多跳接力方式传给汇聚节点,汇聚节点对附近传感器节点信息汇总后通过卫星基站、互联网传送给管理用户[1]。由于传感器节点一般可移动部署以适应环境变化,如何精确定位传感器节点坐标成为WSN研究的热点和难点。
1 WSN定位算法分类
无线传感器网络节点定位算法分为基于测距和无需测距算法两类[2]。对于大部分传感节点而言,当定位误差小于节点通信半径的40%时,定位误差对节点精确度的影响不大[2]。若使用测距定位不仅要配备额外硬件设备,增加节点成本,还会加重电源补给负荷。无需测距算法通过节点之间通信估算彼此之间距离、定位节点坐标,简单方便,得到广泛应用。其中最为经典的是DV-Hop算法。
2 DV-Hop算法
DV-Hop称为距离向量跳段定位算法,用网络平均跳距和节点间最短跳数乘积表示节点之间距离,再利用大量冗余信息节点实现定位。整个过程分为3个阶段:
(1)计算抵达邻居节点跳数。传感节点定期向邻居节点交换抵达网络中其他节点距离,以跳数为单位。最终每个传感节点{xi,yi}都获得自身参考节点跳数hi及参考坐标{xi,yi,hi}。
(2)每个传感节点使用式(1)计算到达其他参考节点的距离。

(3)传感节点得到与其他参考节点距离后,通过三角或多边测量建立方程组,最后利用最小二乘法求解方程组获得节点坐标。
DV-Hop实现简单、方便快捷,但算法中的距离通过节点跳数乘以网络平均跳距得出[3],不可避免地存在误差,加上最小二乘法求解精度依赖于网络跳距初始参数,导致产生的误差呈指数增长、定位精度不高,并且节点密度越低,拓扑越不规则,误差越大。
3 基于粒子群定位算法思想
传感节点记为P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),根据DV-Hop前两阶段估算的抵达网络其他节点距离分别是d1,d2…,dn,估算距离与真实距离之间差值分别为ε1,ε2,…,εn,得以下方程组:

传感节点坐标应同时满足式(2)方程组要求,若|ε1|+|ε2|+…+|εn|和越小,则节点坐标越优、定位越精确,从而可利用最小二乘法求解过程转换为使用粒子群算法求解全局最小最优解的问题,如式(3)所示。

本文提出将粒子群(PSO)离散算法替代DV-Hop中的最小二乘法,用于求解节点最优坐标,既可以发挥PSO全局搜索能力,又可以避免标准PSO算法中过早收敛问题,由此减小网络跳距误差对定位精度的影响范围。
4 标准粒子群算法
粒子群算法是基于鸟类群体行为研究的模拟算法。鸟群在封闭空间随机搜索食物,并且在这个空间只有一个全局最优值[4]。假如所有鸟只都知道当前位置与搜索食物之间的距离,那么找到全局最优解的最优方案就是从身边最近的鸟周围区域进行搜寻[5]。在粒子群算法中,寻找最优问题的每个解对应搜索空间的每只鸟,称为粒子。每个粒子的初始化向量代表鸟的飞行位置和速率,每个粒子通过寻找附近粒子迭代搜寻最优解,具体算法如下:
假设在一个d维搜索空间中,有n个粒子组成的粒子群X=(X1,X2,…,Xn)T,其中第i个粒子位置为Xi=(Xi1,Xi2,…,XiD)T,速率为Vi=(Vi1,Vi2,…,Vid)T,极值为Pi=(Pi1,Pi2,…,Pid)T,种群全局极值为Pg=(Pg1,Pg2,…,Pgd)T,每个粒子找到下一粒子后按以下公式更新当前位置和速率[6]:
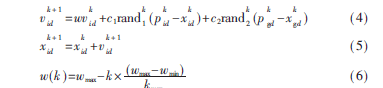
其中,k表示迭代次数,c1、c2为加速系数,rand是[0,1]区间选取的随机数,p是第i个粒子的个体极值在第d维的分量,p是群体全局极值在第d维的分量,x、v分别是第i个粒子经k次迭代后的第d维位置和速率,w是粒子保持运动惯性权重。粒子通过不断更新当前位置和速率最终找到全局最优解,完成搜索过程。
5 新算法定位模型
5.1 离散粒子群算法
粒子群算法前期收敛速率快,但容易出现前期局部最优、后期收敛缓慢的问题。改进离散粒子群算法在于更新粒子当前位置和速率前引入离散运动方程式:
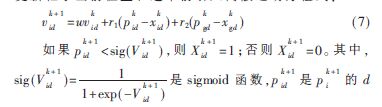
d维分量。粒子的位置只有“0”、“1”两种状态,速率越小,粒子取“0”几率越大,反之取“1”。改进离散粒子群算法使得函数sig(V)不会过于接近“0”或“1”,保证算法以一定概率从一种状态跃迁到另一种状态,从而避免算法过早收敛,出现局部最优现象。
5.2 新算法适应度值选择
新算法通过估计的距离与真实距离之间的差值ε1+ε2+…+εn之和判断粒子所处位置优劣,以此确定是否符合全局最优解要求。差值之和越小,适应度值越大。求解适应度公式为:
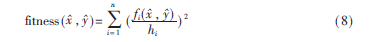
其中,n为传感节点数量;hi为传感节点抵达网络其他节点跳数,由DV-Hop算法第一阶段获得。由于传感节点跳数越多,误差累积越大,因此在计算适应度时加入权重,hi越大的传感节点对适应值影响越小。
5.3 新算法粒子聚集度
在标准PSO算法中,两个粒子之间的距离表示其相似程度大小,距离越近相似度越高。新算法用s(i,j)表示粒子i和粒子j之间的相似度,满足以下条件:
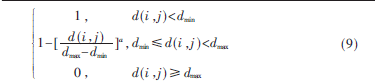
其中,d(i,j)为粒子i和粒子j之间的距离,dmin、dmax表示所有粒子之间距离的最小值和最大值。随着迭代次数增多,粒子适应度越大,与最优粒子相似度越高,位置越趋于全局最优解,最终聚集在一起。新算法聚集度为:

其中,C(t)是粒子群经t次迭代的聚集度,m为种群规模。种群聚集度最密的粒子群收敛于当前全局最优解。
5.4 新算法定位流程
新算法采用改进PSO离散算法替代DV-Hop算法中第3阶段的最小二乘法,利用离散PSO迭代求解避免网络跳距误差对定位精度带来的影响,并得到3个全局体极值的几何质心解,最后计算传感节点坐标。具体步骤如下。
(1)基于DV-Hop算法第1阶段和第2阶段,传感节点间通过与邻居节点通信获得自身参考坐标{xi,yi,hi},并计算抵达网络其他节点距离。
(2)根据网络节点规模和区域大小初始化种群,计算每个粒子适应度,每个粒子位置都是节点定位坐标的可行解。
(3)根据适应度大小更新粒子个体极值,同时找出全局适应度最好的3个个体极值保存在近优解集合中。
(4)根据粒子速率利用离散运动方程式(7)对粒子群状态进行跃迁,避免算法过早收敛。
(5)根据式(4)重新计算粒子当前位置和速率。
(6)根据式(9)计算每个粒子与全局近优解相似度,并根据式(10)计算当前迭代种群的聚集度。
(7)判断是否满足结束条件(达到最大迭代次数或保存近优数组中的3个个体极值都达到最优要求),结束迭代循环,获得3个全局体极值坐标,否则跳到步骤(3)。
(8)通过极值几何质心坐标计算定位传感节点位置。
6 仿真测试
6.1 仿真环境
仿真环境设为100 m×100 m二维区域,节点通信半径为20 m,传感节点比例为80%,初始化粒子群规模200,最大迭代次数500,惯性权重Wmax=0.9,Wmin=0.4,平均定位误差评价为:
6.2 定位误差分析
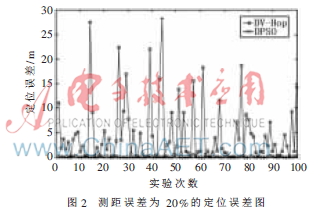
新算法用PSO离散(DPSO)算法替代DV-Hop中的最小二乘法以计算节点坐标,减小DV-Hop网络跳距误差对定位精度的影响。在相同网络环境下,新算法在测距误差为 20%的定位误差明显小于DV-Hop算法,如图2所示。
6.3 标准偏差分析
在测距误差逐渐增加时,开始两种算法定位标准偏差都有所增长,但新算法相比DV-Hop中的标准偏差增长更为缓慢,如图3所示。因为新算法误差增长受节点平均距离误差影响,而DV-Hop算法误差激增是由于最小二乘法对节点平均距离误差放大的结果。当新算法测距误差增长到10%时,标准偏差开始降低,这是由于在计算适应度时加入权重,hi越大的传感节点对适应值影响越小,节点平均距离误差随节点距离增长影响越弱,最大测距标准偏差收敛于2 m以内,可见新算法在定位平均测距误差较大的情况下更具优势。

6.4 收敛性分析
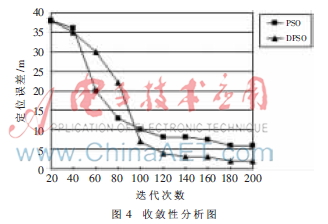
与标准PSO算法相比,两种算法定位误差都随迭代次数增多而减小,如图4所示。在迭代次数较少时两种算法误差较大,这是因为粒子群初始化过程中粒子分布随机性造成的。标准PSO算法在迭代次数达到100时,曲线趋于平稳,定位误差起伏不大,算法开始收敛,但定位误差明显大于新算法,由此推断算法过早收敛陷入局部最优解。而新算法在迭代次数达到120时,定位误差才接近最优解,最终定位误差收敛于2 m以内,这与图3实验数据一致。
本文采用粒子群离散算法替代DV-Hop算法中的最小二乘法,避免网络跳距估计误差对定位精度带来的影响。接下来的工作将着眼于减少算法复杂度,降低无线传感网络能耗问题,以减少实际部署中对环境的依赖程度。
参考文献
[1] NICULESCU D.Localized positioning in ad-hoc networks[J].IEEE International Workshop on Sensor Network Protocols and Applications,2003,1(2):42-50.
[2] PATWARI N.Relative location estimation in wireless sensor networks[J].IEEE Transactions on Signal Processing,2003,51(8):2137-2148.
[3] RANDOLPH.A self-localization method for wireless sensor networks[J].EURASIP Journal on Applied Signal Processing,2003(4):348-358.
[4] LANGENDOEN K.Distributed localization in wireless sensornetworks[J].Computer Networks.2003,43(4):499-518.
[5] GUSTAFSSON F.Mobile positioning using wireless networks[J].IEEE Signal Processing Magazine,2005,22(4):41-53.
[6] YEDAVALLI K.Sequence-based localization in wireless sensor networks[J].IEEE Transactions on Mobile Computing,2008,7(1):81-94.

