摘 要: 针对目前Hadoop平台不能高效处理海量小文件而出现的小文件问题,提出一种基于曲线拟合最小二乘法的确定Hadoop平台下何为小文件的方法。该方法首先确定小文件访问时间的量化方法,然后采用访问时间作为确立何为小文件的影响因子,通过对不同数据集大小的不同访问时间的实验,最终结合线性拟合的相关知识找到了小文件大小的量化方法。
关键词: Hadoop;小文件问题;曲线拟合的最小二乘法;线性拟合
Hadoop[1]是一个具有高扩展性、高可靠性、高容错性和高效性的开源软件系统,它已成为互联网、金融、生物信息学等领域进行大数据分析和处理的代表性云计算平台。它由Hadoop Distributed File System(HDFS)[2]和MapReduce[3]两部分组成,其中,MapReduce主要用来处理数据密集型数据,而HDFS则主要负责大数据的存储。
HDFS的产生得益于Google File System(GFS)[4],它遵循一次写、多次读的流数据访问模式,采用Master-Slave架构,其中的Master,即NameNode,作为单一的节点来管理整个文件系统中所存储数据的元数据。为了快速响应客户端的读写请求,NameNode将文件的元数据存放在内存当中。HDFS设计之初就是为了处理海量大文件的,因此,它能高效地存储和处理海量大文件的读写请求。然而,HDFS不能高效地处理海量小文件,小文件问题[5]由此产生。目前,学术界关注的小文件问题有:(1)海量小文件耗费主节点内存;(2)海量小文件的I/O效率低,没有一种优化机制来提高I/O性能;(3)HDFS下没有明确的能够区分何为小文件的大小文件分界点;(4)海量小文件的放置未考虑文件相关性[6]。针对大小文件的分界点问题提出一种确定何为小文件的方法。在深入研究HDFS存储和访问机制的基础上,经过海量小文件访问、指数拟合和线性拟合等过程,确定了大小文件的临界点。
1 相关研究
Hadoop集群分为NameNode和DataNode两部分,NameNode负责HDFS中文件元数据的存放和对客户端访问的控制,DataNode则负责提供块存储,为客户端的I/O请求提供服务,并根据NameNode的指令执行块的读写操作。其中,NameNode为了向客户端高效地提供元数据信息,将每个文件的元数据信息都存放在内存当中,包括文件名、相应文件对应的块号以及持有这些块的DataNode信息。因此,当客户端请求创建、读、写和删除等操作时,客户端都需要先向主节点查询元数据信息,然后跟相应的数据节点交互,执行需要的操作。
然而,NameNode节点是单一的,其对应的内存大小也是固定的,当一个大于文件块大小的文件存储到HDFS中时,产生的元数据仅仅由文件大小决定,但当海量小文件存储到HDFS中时,每个小文件都会形成一个文件块,因此会产生相当大的元数据信息,例如,假设一个文件的文件块会产生150 B的元数据信息,对于1GB的文件,会被分成16个大小为64 MB的块,此时会产生2.4KB的元数据,然而,对于10 600个大小为100 KB的文件(总大小1 GB),这种情况下将会产生1.5 MB的元数据信息。因此,海量小文件会占用大量的主节点内存,进而当处理海量小文件时,单一的主节点内存就会成为瓶颈,进而影响小文件的存储和访问性能,小文件问题由此而生。
参考文献[7]指出小文件就是那些文件大小明显小于HDFS默认块大小64 MB的文件,海量小文件的产生会限制许多包含大量小文件的应用获益于Hadoop平台。Liu等人[8]针对包含大量小文件的典型应用WebGIS,提出了一种基于HDFS的提升小文件I/O性能的方法。基本思想就是通过小文件合并成大文件来减少文件的数目,然后为每个文件建立索引,同时考虑WebGIS的文件相关特征。实验表明,该方法确实能够提高Hadoop处理WebGIS下相关小文件的处理性能,但它们将文件大小小于16 MB的文件作为小文件,并且没有具体的理论分析和实验来证明16 MB就是大小文件的临界值。
2 小文件量化过程
2.1 Hadoop下小文件访问时间量化
当从HDFS中访问一个文件时,访问过程如下。
(1)客户端通过初始化RPC(Remote Procedure Calls)[9]请求向NameNode发送读指令,其时间开销记为tCN;
(2)NameNode在内存中查询相应文件的元数据,时间开销记为tmetadata;
(3)所需文件的元数据返回到客户端,时间开销记为tNC;
(4)客户端向相关DataNode发送读取指令,时间开销记为tCD;
(5)DataNode从磁盘中取出所需文件的文件块,时间开销记为tdisk;
(6)所需文件的相应文件块返回到客户端,所需时间记为tnetwork。
其中,因为tCN和tCD是发送指令所带来的开销,通常作为常量;同时,由于元数据非常小,tmetadata也可以当做常量;tnetwork与所读取文件的长度(L)和网络传输速度(V)有关,因此,它可以表示为δnetwork(L/V)。
假设有N个不同的小文件,文件长度分别表示为L1,L2,L3,…,Ln,那么N个文件的访问时间可以表示为:
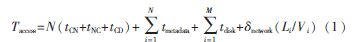
其中,因为对于小文件来讲,每一个文件仅仅有一个块,所以读取块数和文件的个数是相等的,即M和N相等,那么式(1)还可表示为:
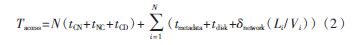
2.2 文件随机访问算法
文件随机访问算法通过N来控制随机数的产生个数,进而来控制随机访问的文件,然后调用HDFS提供的访问API来获取分布式文件系统中存放的文件,最终返回访问指定文件个数的文件所需要的时间,具体算法伪代码如下。
Input:SmallFile
Output:AccessTime
Create a collection//创建一个集合
getConfiguration()//获取HDFS必要的文件配置信息
for(int i=0;i<N;i++){
//N为随机下载的文件个数
int j=getRandom()//获取一个随机数
add(j)//将随机数添加到集合中
}
collectionIterator();//创建一个迭代器
Long t1=getStarttime()
while(iterator.hasNextNumber){
getNextValue()//获取迭代器中的随机数
Path src//HDFS中符合相应随机数的文件路径
Path dst//访问随机文件的存放路径
copyToLocalFile(src,dst)
}
Close()//关闭分布式文件系统
long t2=getStopTime()
output(“AceessTime”,t2-t1)
2.3 曲线拟合的最小二乘法
若要求一个函数y=S*(x)与所给数据{(xi,yi),i=0,1,…,m}拟合,若记误差δi=y-S*(xi)-yi(i=0,1,…,m),δ=(δ0,δ1,…,δm)T,设?渍0(x),?渍1(x),…,?渍n(x)是C[a,b]上线性无关函数族,在?渍=span{?渍0(x),?渍1(x),…,?渍n(x)}中找一个函数S*(x),使误差平方和

以上就是一般的最小二乘逼近,用几何语言说,就成为曲线拟合的最小二乘法[10]。
3 实验结果与分析
3.1 实验环境
实验所用Hadoop平台包含6台PC,其中1台作为NameNode,其他5台为DataNode,每台机器的配置为:Intel Core 2(2.99 GHz)处理器,2 GB内存,160 GB硬盘。
所有节点均连接在1.0 Gb/s的以太网中。每台机器的软件环境为:操作系统采用内核为3.5.0-25的Ubuntu 12.04,集群的Hadoop版本为1.1.2,Java版本是JDK 7.0。
其中HDFS的默认副本数为3,块大小默认为64 MB。
3.2 数据集
实验所采用的数据集共有23个,数据集内容来自于China Daily的新闻稿,各个数据集分别命名为ds1,ds2,…ds23。每个数据集分别包含10 000个文件,数据集大小有0.5 MB~64 MB不等,具体分布情况如图1所示。

3.3 实验方法
分别将上述数据集上传到空白的HDFS中,然后采用上文所提到的文件随机访问算法随机获取500个文件到本地文件系统,同时记录下程序反馈的每个数据集的访问时间。
每个数据集的访问时间测试分别进行7次,然后舍弃其中的两个最大值和两个最小值,剩余的3组值取平均,最后以平均值作为每个数据集的实验所得访问时间。通过这种方法来过滤掉因网络拥塞或者其他未知因素导致的噪声点。
测得每组数据的平均访问时间后,分别计算每组数据集的平均访问速率,当HDFS默认块大小为64 MB时,其访问速率与文件大小在曲线拟合后的关系如图2所示。
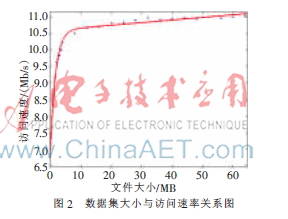
根据图2图像的变化规律可知,小文件数据集的访问速率在一定范围内变化显著,随着数据集文件大小的增大,变化逐步趋于平缓。根据指数函数的特性,为了更好地观察其变化规律,分别对x和y轴取对数,由图3可明显地看到前8个数据点在一条直线上,而除此之外的其他数据点在另外的直线上,然后采用线性拟合的方法,得到两直线交点,进而得到对应直线交点的文件大小为4.38 MB。


此外,针对dfs.blocksize默认块大小为48 MB的情况也进行相同的实验,得到的结果如图4所示。其中,文件块大小为48 MB的线性拟合后直线交点处所对应的文件临界值大小为4.41,很明显,文件块大小在64 MB和48 MB两种情况下,这个临界点文件大小几乎相同,由此确定了大小文件的临界值大小。
提出一种确定Hadoop平台下大小文件分界点的方法,该方法首先确定了Hadoop平台下小文件的访问时间量化方法,然后通过客户端随机访问HDFS中不同大小数据集的不同访问时间,并且结合曲线拟合的最小二乘法相关知识,通过实验找到了大小文件的临界点。今后的工作将考虑通过对其他相关因子的量化来进一步细化该临界点的获取方法。此外,计划在结合大小文件的临界点问题的基础上,针对小文件问题进行进一步研究,并且结合文件合并、文件的分布式索引和相应的缓存预提取等机制来优化Hadoop平台下海量小文件的读取和存储性能。
参考文献
[1] WHITE T. Hadoop: The Definitive Guide, 2nd[M]. California: O′Reilly Media, 2009.
[2] SHVACHKO K, KUANG H, RADIA S, et al. The hadoop distributed file system[C]. Proceedings of IEEE 26th Symposium on Mass Storage Systems and Technologies, Incline Village, USA: IEEE Press,2010:1-10.
[3] DEAN J, GHEMAWAT S. MapReduce: simplified data processing on large clusters[J]. Communications of the ACM,2008, 51(1):107-111.
[4] SEHRISH S, MACKEY G, WANG J, et al. MRAP: a novel MapReduce-based framework to support HPC analytics applications with access patterns[C]. Proceedings of the 19th ACM International Symposium on High Performance Distributed Computing. New York, USA: ACM Press, 2010:107-118.
[5] Liu Xiaojun, Xu Zhengquan, Gu Xin. Study on the small files problem of Hadoop[C]. Proceedings of 2012 IEEE 2nd International Conference on Cloud Computing and Intelligence Systems, Hangzhou, China: IEEE Press,2012:278-281.
[6] DONG B, QIU J, ZHENG Q, et al. A novel approach to improving the efficiency of storing and accessing small files on hadoop: A case study by PowerPoint files[C]. Proceedings of the IEEE International Conference on Services Computing. Florida, USA: IEEE Press,2010:65-72.
[7] The small files problem[EB/OL]. http://www.cloudera.com/blog/2009/02/the-smallfiles-problem/,2009.
[8] Liu X, Han J, Zhong Y, et al. Implementing WebGIS on Hadoop: a case study of improving small file I/O Performance on HDFS[C]. Proceedings of the IEEE international conference on cluster computing and workshops. New Orleans, USA: IEEE Press,2009:1-8.
[9] CHANDRASEKAR S, DAKSHINAMURTHY R, SESHAK-UMAR P G, et al. A novel indexing scheme for efficient handling of small files in Hadoop distributed file system[C]. Proceedings of the International Conference on Computer Communication and Informatics. Coimbatore, USA: IEEE Press,2013: 1-8.
[10] 陈珂,邹权.融入时间关联因子曲线拟合的交通流异常挖掘方法[J].计算机工程与设计,2013,34(7):2561-2565.

