摘  要： 为了提高伽罗瓦连接所有不动点的计算速度和效率，在计算伽罗瓦连接不动点的串行算法（CbO）基础上，通过处理所有不动点的不相交子集方法，将串行算法并行化，启动P个处理器同时并行运行，使每个处理器都并行地计算它的所有不动点，证明了此算法的正确性，并分析了它的渐近式复杂性。实验给出了算法在各种数据集上的效率及可扩展性，表明PCbO并行算法效率优于其串行算法。

　　关键词： 伽罗瓦连接；不动点；形式概念分析；并行算法

0 引言

　　本文提出了计算伽罗瓦连接所有不动点的一个并行算法，其中伽罗瓦连接是由对象属性关联数据引起的，称为形式概念的不动点表示可以在数据中找到的基本矩形模式。除了它们的几何意义，可以将不动点解释为在输入关联数据中发现的自然概念的形式化。每个形式概念由它的外延（即属于概念的所有对象集）和内涵（即由概念所涵盖的所有属性集）给出。用一个子概念-超概念序列装配的所有形式概念集形成了一个完整的晶格，通常称为一个概念格。概念格和有关的关联结构由形式概念分析深入研究，这是20世纪80年代早期由鲁道天（Rudolf Wille）成立的一个学科，从此出现了许多理论成果和形式概念分析（FCA）的应用程序[1-2]。在FCA的任何应用中所出现的基本任务就是输入相关的数据并计算所有形式概念集。本文通过将所有形式概念分成不相交的子集，从而对概念进行并行化计算，有助于FCA的一系列算法。

　　本文首先介绍形式概念分析的概念，然后提出了伽罗瓦连接不动点的并行算法并证明其正确性，最后讨论了并行算法的复杂性、效率及可扩展性。

1 基本概念

　　首先介绍一下形式概念分析的基本概念，更多细节参阅参考文献[1-3]。设X={0，1，…，m}和Y={0，1，…，n}分别代表对象和属性的有限非空集。一个形式上下文是一个三元组<X，Y，I>，其中I?哿X×Y，即I是X和Y之间的一个二进制关系。如给定<X，Y，I>，一对概念形式运算符[1]↑I：2X→2Y和↓I：2Y→2X已定义，对于每个A?哿X和B?哿Y，分别通过A↑I={y∈Y|对每个x∈A：<x，y>∈I}和B↓I={x∈X|对每个y∈B：<x，y>∈I}。（以下省略I，只写↑和↓分别代替↑I和↓I。）通过具有外延A和内涵B的一个形式概念（在<X，Y，I>），可以表示任何对<A，B>∈2X×2Y，致使A↑I=B和B↓I=A。这样形式概念是概念形式运算符的不动点，<↑I，↓I>的所有不动点集合由B（X，Y，I）表示。在<X，Y，I>中，所有形式概念集合B（X，Y，I）用一个偏序关系≤表示，该偏序关系≤模拟子概念超概念层次：

　　如果A1A2（或B1B2），则<A1，B1>≤<A2，B2>（1）

　　如果<A1，B1>≤<A2，B2>，那么<A1，B1>称为<A2，B2>的一个子概念。由式（1）定义和≤在一起的集合B（X，Y，I）形成了一个完整的格，它的结构由FCA的基本定理来描述[1]。

2 计算所有不动点的算法

　　并行算法可以看作是在概念的不相交子集上同时工作的几个串行版本的实例，对于一个给定的形式上下文<X，Y，I>，集中<↑I，↓I>的所有不动点，以致于X={0，1，…，m}和Y={0，1，…，n}）。

　　2.1 串行算法

　　串行算法的核心是一个递归过程GenerateFrom，如算法1列出了通过形式概念空间进行深度优先搜索的所有形式概念。这个过程将一个初始形式概念<A，B>和一个属性（所处理的第一个属性）作为它的自变量。用形式概念<A，B>开始，这个过程通过形式概念空间递归下去。当用<A，B>和y∈Y调用时，GenerateFrom先处理过程<A，B>，然后检查它的停机条件。根据停机条件，当<A，B>等于<Y↓，Y>或y>n时，计算停止；否则，这个过程用完所有属性j∈Y，以致于j≥y不包括在内涵B中，对于每个有这些属性，一对<C，D>∈2X×2Y以致于可以计算：

　　<C，D>=<A∩{j}↓，（A∩{j}↑）>（2）

　　<C，D>总是一个形式概念，以致于B?奂D，在得到<C，D>后，算法检查它是否应该用<C，D>继续递归地调用GenerateFrom或是否跳过<C，D>，这个测试基于比较B∩Yj=D∩Yj而Yj?哿Y按如下定义：

　　Yj={y∈Y|y<j>}（3）

　　算法1 Procedure GenerateFrom（<A，B>，y）

　　Input：formal concept<A，B>and a number y∈Y∪{n+1}such that y?埸B

　　1  process<A，B>（e.g.，print<A，B>on the screen）；

　　2  if B=Y or y>n then

　　3    return

　　4  end

　　5  for j from y upto n do

　　6    if j?埸B then

　　7      set C to A∩{j}↓；

　　8      set D to C↑；

　　9      if B∩Yj=D∩Yj then

　　10       GENERATEFROM（<C，D>，j+1）

　　11     end

　　12   end

　　13 end

　　14 return

　　为了证明算法1的正确性，引入了与过程GenerateFrom递归调用相对应的推导。后面使用这个推导描述并行算法。

　　定义1（形式概念推导）若<X，Y，I>是一个形式上下文，具有Y={0，1，…，n}，对于形式概念<A1，B1>，<A2，B2>∈B（X，Y，I），整数y1，y2∈Y∪{n+1}使<<A1，B1>，y1>├─<<A2，B2>，y2>表示 m=y2-1必须满足以下所有条件：（1）m?埸B1；（2）y1<y2；（3）B2=（B1∪{m}）↓↑；（4）B1∩Ym=B2∩Ym，其中Ym由式（3）定义。

　　长度为k+1的<A，B>∈B（X，Y，I）的一个推导是以下任何序列：

　　<<0>=<<A0，B0>，y0>，<<A1，B1>，y1>，…，<<Ak，Bk>，yk>=<<A，B>，yk>（4）

　　以致于对于每个i=0，…，k-1都有<<Ai，Bi>，yi>├─<<Ai+1，Bi+1>，yi+1>。如果<A，B>有一个长度为k的推导，<A，B>是k步可推导的。如果GENERATEFROM（<A，B>，y）的调用引起第10行调用GENERATEFROM（<C，D>，k），显而易见<<A，B>，y>├<<C，D>，k>确实地：（1）确保算法1第6行的条件得到满足；（2）对应到5~13行之间的循环（从y向上的）；（3）是在8行所计算的内涵。如果第9行的条件是正确的，那么（4）是真的。

　　下面的论断显示了推导的存在性和唯一性。

　　引理1（推导的存在性）对于每个形式概念<A，B>∈B（X，Y，I）有一个推导（4），以致于yi=mi+1，其中对于每个0<i≤k，都有：

　　mi=min{y∈B|y?埸Bi-1}（5）

　　引理2（推导的唯一性）每个形式概念<A，B>∈   B（X，Y，I）至多有一个推导。

　　从引理1和引理2可以得到下面的结论：

　　定理1（算法1的正确性）：当用y=0调用时，算法1导出了<X，Y，I>中的所有形式概念，且它们中的每一个仅有一次。

　　算法1通过一个递归过程GenerateFrom而不是通过回溯法来表达CbO（Close-by-One）算法[4]。这有几个好处：（1）GenerateFrom比参考文献[4]的抽象描述更接近实际的实现。（2）对已经处理过的属性无需作明确的标注[4]。这是因为GenerateFrom的每次调用在一个局部变量j中都有所有必要的信息。当计算新的闭包时，通过Y的所有属性的一个子集来提高这个算法的效率。（3）无需建立CbO树作为一个数据结构，CbO树与GenerateFrom的递归调用相对应：定义1的推导对应到CbO树中典型路径[4]。

　　2.2 并行算法

　　假设有能同时执行指令的P个独立的处理器，这些可能表示在一个网络中的独立计算机或者是在一个共享内存系统中的多处理器。每个处理器可以处理上下文<X，Y，I>，因为<X，Y，I>在计算期间不允许修改，每个处理器可以有<X，Y，I>的拷贝或在多个处理器间共享一个拷贝。本文所提出的并行算法主要是对GenerateFrom的修改，以致于由P个处理器同时处理调用树的特殊子树。根据定义1，算法首先处理用少于L步就可推导的所有概念，剩余的概念采用并行方法处理。因此计算概念的一个并行过程可以概括为以下三个相续的阶段：

　　（1）计算并处理用少于L步可推导的所有概念；

　　（2）将用L步可推导的所有概念存储在P个独立的队列中；

　　（3）启动P个处理器，运行并行计算：①使每个处理器占有一个队列；②使每个处理器计算在它的队列里的所有概念。

　　一个并行算法由过程ParallelGenerateFrom表示，见算法2。在计算过程中，算法2有两个常参数是很重要的，即P≥1（处理器的数量）和L≥2（递归的层数）。P和L值的选择对算法的实际性能有影响，过程ParallelGenerateFrom是GenerateFrom的一个修改，并接收了一个附加的变量：计数值l从1到L，表示在第1阶段处理的推导的长度。在它启动后，ParallelGenerateFrom按如下进行：模拟原始GenerateFrom直到它达到了L递归层，见第1~17行之间的代码。这与以上第1阶段概述一致。

　　算法2 Procedure ParallelGenerateFrom（<A，B>，y，l）

　　Input：formal concept<A，B>

　　number y∈Y∪{n+1} such that yB

　　level of recursion L≥2

　　number of processors P≥1，and

　　counter l such that 1≤l≤L

　　1  if l=L then

　　2    select r∈{1，…，P}；

　　3    store<<A，B>，y>to queurer；

　　4    return

　　5  end

　　6  process<A，B>（e.g.，print<A，B>on screen）；

　　7  if not（B=Y or y>n）then

　　8    for j from y upto n do

　　9      if jB then

　　10       set C to A∩{j}↓；

　　11       set D to C↑；

　　12       if B∩Yj=D∩Yj then

　　13         PARALLELGENERATEFROM（<C，D>，j+1，l+1）；

　　14       end

　　15     end

　　16   end

　　17 end

　　18 if l=1 then

　　19   for r from 1 upto P do

　　20     with processor r

　　21       foreach <<C，D>，j>∈queuer do

　　22         GENERATEFROM（<C，D>，j）；

　　23       end

　　24     end

　　25   wait for all processors

　　27 end

　　28 return

　　算法2的关键问题是如何分配在L步可推导的形式概念进入P个队列。通过选择放<<C，D>，y>的一个队列，选择将列出所有形式概念后项的一个处理器到 <C，D>，最优的选择方法应该是将所有的形式概念均匀地分配到处理器。然而，这是很难完成的，因为直到实际计算并显示出调用树的结构后才知道在所有形式概念的研究空间中形式概念的分配情况。这个算法选择基于一个简单循环原则的queuer，r=（N mod P）+1，其中N为到目前为止所存储的形式概念数。

　　本文的算法有两个部分：一部分将概念分配进队列，另一部分以并行形式运行几个普通的Close-by-One。下面给出了PCbO的正确性。

　　定理2（PCbO的正确性），y=0和l=1调用时，算法2导出了<X，Y，I>中的所有形式概念，且它们中的每一个仅有一次。

　　算法2的参数P和L对所计算的形式概念在处理器中的分配有影响，参数P的实际范围是由所运行算法的硬件限制（由硬件处理器或网络节点限制），而L设成≥2的任何值。L值依赖的算法性能在后文由实验评价，如果L=2，大多数形式概念由一两个处理器计算，随着L值增加，形式概念均匀地分配到更多的处理器上。大的L值会退化并行计算，例如，如果L≥|Y|+1，则所有的概念将在第1阶段按次序地计算，因为调用树的深度最多是|Y|+1，从经验看，假如|Y|是大的，平均一个好的权衡值是L=3。在这种情况下，几乎所有形式概念并行计算并最优地分配到各处理器上。

3 实验结果

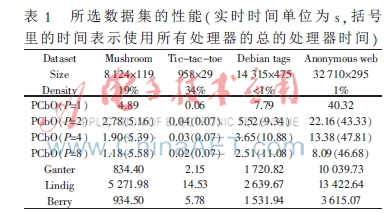
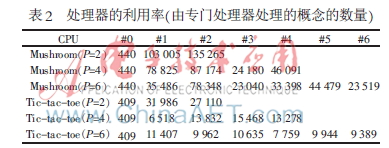
　　从最坏情况下的复杂性角度来看，PCbO是一个渐进复杂性为O（|B||Y|2|X|）的多项式时间延迟算法[5]，因为在最坏情况下PCbO可退化为串行CbO[4，6]，在处理器的最佳利用情况下，PCbO能比CbO快P倍，实际上达不到p倍，因为：（1）概念是不均匀地分布在处理器上的；（2）并行化本身也有一定的开销。本文给出了具有随机生成的一组真实数据集的实验结果，首先把PCbO与其他计算形式概念的算法进行比较，即把它与Ganter、Lindig和Berry的算法进行比较（所有算法都是在ANSI C上实现的）。将参考文献[7]、[8]使用的数据集与Debian GNU/Linux软件包描述产生的数据集进行比较。有关使用数据集的规模和密度信息结果如表1所示，前4行是在1、2、4和8个处理器上运行的PCbO运行时间。测量是在具有8个独立处理器空闲的64位硬件上进行的。对于P>1，表1中包含计算所有形式概念的总处理器时间。允许对管理多线程计算的开销进行粗略的估计：开销可以通过真实处理器时间减去总处理器时间除以P计算，而更大的P值会导致更大的开销，处理器的利用率可以从由每个处理器处理概念的数量研究。表2显示了特定处理器计算概念间的分布。处理器标号#0是算法的初始阶段，每个处理器计算概念的数量是完全由参数P、L和通过上下文决定的，这意味着如果一个处理器完成计算，它不能帮助其他处理器处理负载。

　　接下来的实验研究PCbO的可扩展性，使用多个处理器减少运行时间的能力。该实验使用配备八核UltraSPARC Ⅱ处理器可以处理多达32个同时运行的线程的计算机。

　　图1（a）包含选定的数据集的结果，而图1（b）包含随机生成的表的结果（具有10 000个对象和5%密度）。纵轴上显示一个相对加速比，理论加速是由硬件处理器数决定的（即如果有4个处理器，执行速度能快4倍）。因此相对加速比是使用单一处理器的运行时间（串行算法）和使用多个处理器的运行时间的比值。加速比的理论最大值等于P，但由于线程管理带来的开销，真正加速比要小些（参见表1）。

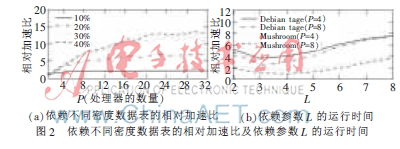
　　图2（a）的实验显示了数据密度的影响结果，已经产生了具有不同密度的数据表，并观察到可扩展性的影响。使用数据表大小为5 000×100，图2（b）说明了在不同数据表和处理器下参数L的影响，实验结果表明，好的选择是L∈{3，4}。该算法实现的实际性能取决于所使用的数据结构，这里已经使用布尔向量作为基本数据结构，并证明此数据结构是非常有效的。计算闭包的数据结构和优化算法需进一步讨论。

4 结论

　　本文提出了一种称为PCbO的并行算法，该算法在对象属性数据表中计算形式概念，并行算法的结果是CbO的并行化和模拟普通CbO的递归过程的形式化。它叉分成多个过程，且每个过程计算形式概念的不相交集。该算法具有最小的开销，因为计算不相交的概念集合的并行进程是完全独立的，这大大提高了算法的效率。该算法是可扩展的，随着CPU数量的增加，通过增加CPU数量计算加速比就接近理论极限。未来的研究将集中在以下几方面：

　　（1）减少计算多次概念的数量；

　　（2）用于选择队列和防止退化计算的先进条件下的各种策略的比较；

　　（3）与其他并行算法的性能比较，各种数据结构的可伸缩性测试的程度和意图；

　　（4）算法的专门变种集中解决有关FCA的特定问题，例如二进制矩阵分解。

　　参考文献

　　[1] GANTER B， WILLE R. Formal concept analysis： mathematical foundations[M]. Berlin： Springer，1999.

　　[2] CARPINETO C， ROMANO G. Concept data analysis： theory and applications[M]. New York： Wiley， 2004.

　　[3] GRATZER G. General Lattice theory（2nd end）[M]. Basel：Birkhauser， 2003.

　　[4] KUZNETSOV S O. Learning of simple conceptual graphs from positive and negative examples[C]. Proceedings of the Third European Conference on Principles and Practice of Knowlege Discovery in Databases， PKDD 1999，1999，1704：384-392.

　　[5] JOHNSON D S， YANNAKAKIS M， PAPADIMITRIOU C H. On generating all maximal independent sets[C]. Information Processing Letters， 1988，27（3），119-123.

　　[6] KUZNETSOV S O. A fast algorithm for computing all intersections of objects in finite semilattice[C]. Automatic Documentation and Mathematical Linguistics，1993，27（5）：11-21.

　　[7] HETTICH S， BAY S D. The UCI KDD Archive.[2014-04-10].http：//kdd.ics.uci.eut. School of Information and Computer Sciences，University of California， Irvine， 1999.

　　[8] ASUNCION A， NEWMAN D. UCI Machine learning repository.[2014-04-10].http：//archive.ics.uci.edu. School of Information and Computer Sciences， University of California， Irvine， 2007.