0 引言

    MIMO-OFDM系统凭借其系统容量大、抗干扰能力强等优点，成为新一代无线通信领域的核心技术^[1-3]。由于MIMO-OFDM对延时和频偏很敏感，为保证接收端能够正确解调，必须要进行时频同步^[2-3]。此外，由于MIMO-OFDM系统中有多根天线，其相互间的干扰使得同步更加困难^[3]。

    文献[4]首次提出使用相互正交的训练序列，将OFDM系统中的SC算法应用到MIMO-OFDM系统中，解决了各天线间的相互干扰问题^[5]。文献[6]利用各天线分时发送训练序列来保证时域上的正交性，但是在天线较多时占用较多时域资源。以上两种方法在时间同步前都需要进行帧检测，补偿频偏后再进行符号同步才能得出正确的定时位置，因而运算量大，并且时间同步性能易受到频偏补偿性能的影响。文献[7]提出了WPS算法，利用CAZAC序列良好的自相关性，使得定时性能有了显著提高，但是没有考虑到频偏对定时位置的影响。文献[8]使用循环的延迟序列，采用互相关和自相关结合的方法进行定时同步，性能良好，但是依然受到频偏影响，在频偏补偿之后需要对定时位置进行修正。本文基于WPS算法，提供了一种改进的前导序列结构和定时同步方法，该方法仅需一步便能完成整个时间同步，定时结果不受频偏影响，而且同时还能估计出整数倍频偏。仿真结果表明，在AWGN信道和多径信道下，该同步方法都具有良好的性能。

1 MIMO-OFDM系统模型

    MIMO-OFDM系统原理框图如图1所示。

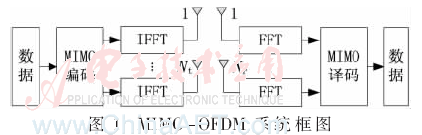
    各发射天线发送的OFDM符号可表示为：

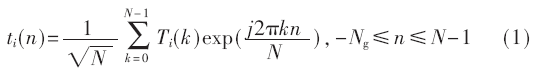
其中，i表示发射天线序号，最大为N_t；N表示IFFT变换的点数，也即系统所用子载波个数；T_i(k)为第i个发射天线、第k个子载波上的调制数据；N_g为消除OFDM符号间干扰的循环前缀的长度。

    在高斯信道下，接收天线接收到的基带信号可表示为：

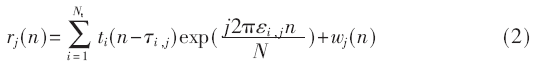
其中，j表示接收天线序号，最大为N_r；τ_i，j和ε_i，j分别表示第i条发射天线到第j条接收天线的时间延迟和频率偏移，?着ij包括整数部分和小数部分，在系统同步过程中需要分别估计；ω_j(n)表示第j根天线上接收到的AWGN总和。

2 时间同步方法分析

2.1 WPS定时同步算法

    图2所示为WPS算法使用的同步序列结构。

    该前导序列由长度为N的CAZAC序列构成。其生成表达式如下^[9]：

    容易看出，CAZAC序列的自相关函数是理想的二值函数，因此将其循环移位后得到的序列和原序列相互正交，保证了各发射天线上的序列正交性。

    由式(3)易知，生成的CAZAC序列还具有自反特性，如下式：

    只有在训练序列起始处，判决函数M_i(d)才能取得最大值，其余位置上的取值均接近于零，如图3(a)所示。可以看出，定时函数的峰值尖锐，很容易得出定时点位置。

    引入频偏?着之后，判决函数峰值虽然依然尖锐，但是峰值点位置会有一定的移位，影响定时点位置的判断，如图3(b)所示。

2.2 改进的前导序列结构和时间同步方案

2.2.1 改进的前导序列结构

    由于WPS算法的定时准确性受频偏的影响，因此对同步序列结构进行一定的改进，采用如图4所示的序列结构。

    该序列占用2个OFDM符号长度，由周期分别为N_c和N的CAZAC序列组成，N=2N_c。各天线上的序列由CAZAC序列循环移位得到。若第1根发射天线上的序列为c(n)，则第i根发射天线上的序列可以表示为c(n-(i-1)·D)，D表示循环移位数。

    当存在频偏ε时，将接收端接收到的信号同本地序列c(n)进行互相关如下：

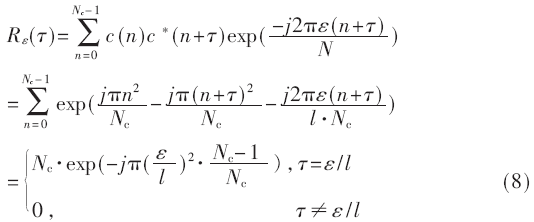
其中l=N/N_c。对比式(5)和式(8)可以看出：当存在频偏时，互相关函数峰值位置相对理想位置有[ε/l]长度的移位。

2.2.2 改进的时间同步算法

    本文提出的方法利用接收信号同本地序列进行互相关来进行定时同步。假设本地序列分别为长度为N_c的c₁(n)和长度为N的c₂(n)，则判决函数可表示为：

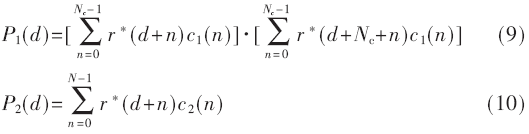
    在P₁(d)和P₂(d)分别取得最大值处即为训练序列c₁(n)和c₂(n)的起始位置处。

    由于信号传输过程中存在频偏ε，由式(8)可知，求得的P₁(d)、P₂(d)的峰值位置相对于理想定时点分别有[ε/2]和[ε]的移位，如图5所示。

    与WPS算法相比，本文采用的方法虽然增加了训练序列的长度，占用了一定的信道资源，但是能够直接地得出准确的定时点，使定时不受频偏影响，并且在定时的同时能够估计出整数倍频偏，缩短了同步过程，从而降低了系统同步的复杂度。

3 仿真与比较

    参考IEEE802.11n标准^[10]，在高斯信道和多径信道下对本文提出的算法和WPS算法分别进行了仿真。天线数为2发1收，更多天线数目的情况可由此推广得到。仿真各参数如表1所示。

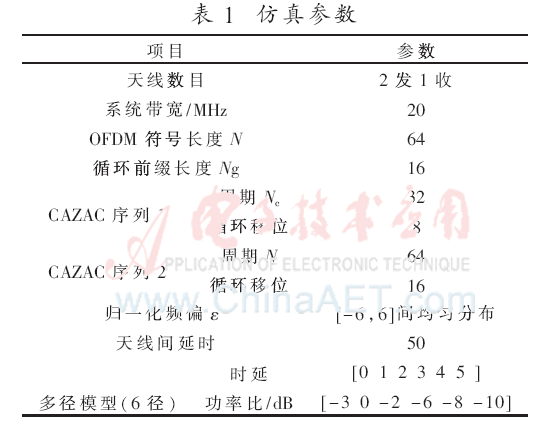
    忽略频偏影响，在单径信道下，对WPS算法和本文提出算法的正确定时概率进行比较，在不同信噪比下的曲线如图6所示。可以看出本文提出的算法定时性能优于WPS算法，尤其在低信噪比条件下更为明显。

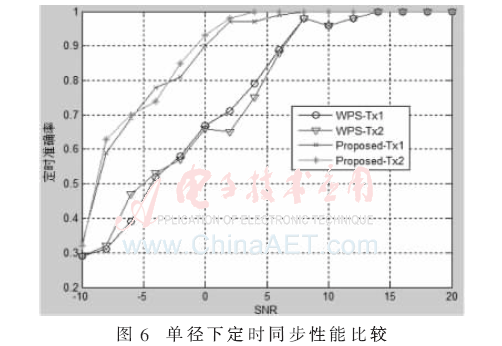
    图7所示分别为在多径条件下，频偏为0、信噪比为10时，WPS算法和本文提出算法的定时判决函数曲线。可以看出，图7(a)中WPS算法在两根发射天线信号处都能产生峰值，但是由于伪峰存在，难以判断定时点的具体位置；图7(b)、图7(c)中，本文提出的算法对两根发射天线信号分别进行判断，虽然判决函数也存在伪峰，但是在最强径定时点上一定取得最大值，伪峰的存在对定时点的判断并没有太大影响。

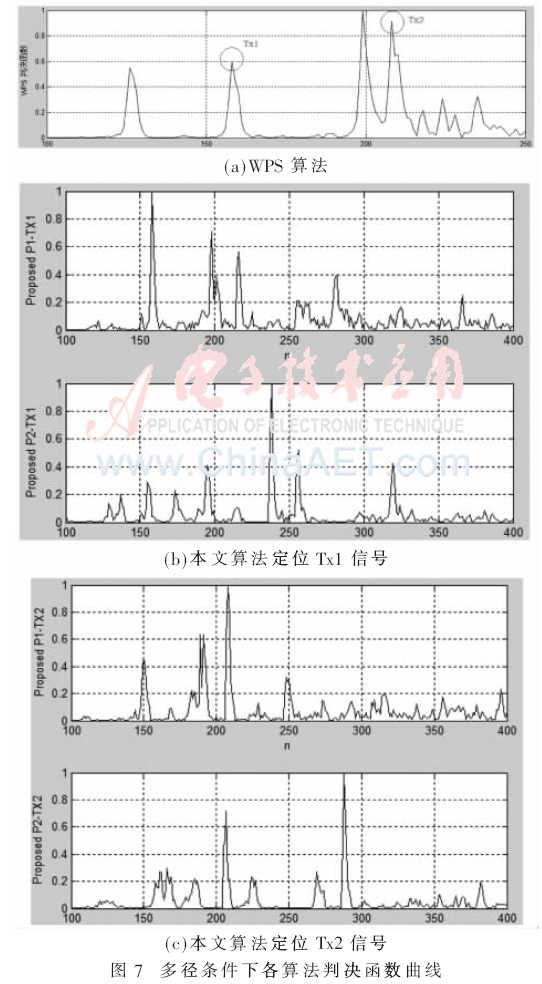
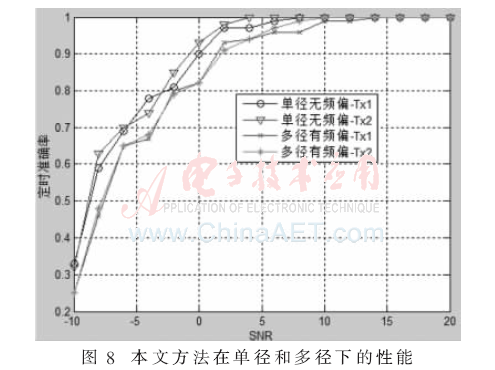
    图8所示为本文提出方法在单径无频偏和多径有频偏下的性能对比。由图中可以看出，算法在多径与单径条件下性能差别不大，多径的存在几乎不对算法性能产生大的影响，同时也可以看出，算法在有频偏的情况下也能正确定时。

4 结束语 

    本文针对MIMO-OFDM系统，提出了一种改进的训练序列结构和定时同步方法。采用不同长度的CAZAC序列构成训练序列，接收时利用本地互相关的方法进行定时同步。虽然增加了训练序列的长度，但是能够直接得出正确的定时点，使定时位置不受频偏影响；并且能同时估计出整数倍频偏，缩短了同步过程，从而降低了系统的复杂度。理论和仿真分析表明，该方法相对WPS算法有着明显的性能提升。

参考文献

[1] CHO YONG SOO，JAEKWON KIM，WON YOUNG YANG，et al.MIMO-OFDM wireless communications with MATLAB[M].John Wiley & Sons，2010.

[2] RACHINI A，BEYDOUN A，NOUVEL F，et al.Timing synchronization method for MIMO-OFDM system using orthogonal preamble[C].Telecommunications(ICT)，2012 19th International Conference on.IEEE，2012：1-5.

[3] WANG HUNG-CHIN，WANG CHIN-LIANG.A compact preamble design for synchronization in distributed MIMO OFDM systems[C].IEEE Vehicular Technology Conference(VTC Fall)，San Francisco，California，USA：IEEE，2011：1-4.

[4] MODY，APURVA N，GORDON L.STUBER.Synchronization for MIMO-OFDM systems[C].Global Telecommunications Conference，2001.GLOBECOM′01.IEEE.San Antonio，USA：IEEE，2001：509-513.

[5] SCHMIDL T M，COX D C.Robust frequency and timing synchronization for OFDM[J].Communications，IEEE Transactions on，1997，45(12)：1613-1621.

[6] VANZELST V，SCHENK T C W.Implementation of a MIMO-OFDM-based wireless LAN system[J].Signal Processing，IEEE Transactions on，2004，52(2)：483-494.

[7] FENG C，ZHANG J，ZHANG Y，et al.A novel timing synchronization method for MIMO OFDM systems[C].Vehicular Technology Conference，2008.VTC Spring 2008.IEEE.Singapore：IEEE，2008：913-917.

[8] 许成谦，刘萌萌．多径衰落信道下MIMO-OFDM系统的定时同步算法[J]．北京邮电大学学报，2012，35(3)：95-98.

[9] HEIMILLER R C．Phase shift pulse codes with good periodiccorrelation properties[J]．Information Theory，IRE Transactions on，1961，7(4)：254-257.

[10] IEEE Std.802.11nTM-2009[S].IEEE STANDARD for Information Technology-Telecommunications and information exchange between systems-Local and metropolitan area networks-Specific requirements.Oct.2009.