0 引言

    由于无线传感网将大量传感器分布于目标区域用来监控目标区域中的可感知状态(温度、高度等)^[1]，因此被广泛应用于工业控制^[2]、农产品生产^[3]及战争^[4]等领域。传感节点一般体积较小、成本低廉，传感节点的能量是一个重要资源。

    文献[5]针对周期性采集数据的传感器网络提出了一种基于分布式的跨层能效优化协议EEDS。EEDS的核心思想是建立一个能量效率树状结构，树的节点为传感器节点，并建立了相应的TDMA调度器^[6]。

    本文基于EEDS协议的能量效率树与调度器建立了跨层优化模型。本算法通过设置目标成本函数，并求解其最优解来获得全局最优生命周期，从而提高了原协议的网络生命期，降低了数据传输的延迟。

1 EEDS协议及其模型简介

    EEDS的核心思想是建立一个联合路由树状结构及TDMA调度器。EEDS协议将每个时间帧分为若干轮，每轮分为3个阶段：建立树状结构(BT)、建立调度器(BS)、数据传输(DT)。BT阶段：建立以sink节点为根的树状结构；BS阶段：建立一个分布式TDMA调度器；DT阶段：将数据从源节点传输至sink节点。每轮中的3个阶段重复多次，如图1所示。

1.1 建立能量效率树状结构

    采用文献[7]的算法建立能效树状结构。首先，初始化sink节点并广播控制信息，控制信息由4部分组成：状态、深度、父节点、剩余能量值。

1.2 建立TDMA调度阶段

    基于第一阶段建立的能量效率树，建立TDMA调度器。设TRR、TRT为2个关于节点的时间常量：对于一个节点v，TRR_v表示该节点准备好接收其子节点信息的时间间隙长度，TRT_v表示该节点准备好向其子节点发送信息的时间间隙。因此节点在时间段[TRR_v，TRR_v+1]内必须处于唤醒状态。设t′表示时间间隙，在该时间间隙内节点采集数据并向父节点传输数据。然后，因叶节点无子节点，所以叶节点的TRRv无效；对于非叶节点v，可表示为：

2 基于线性规划问题EEDS协议优化模型(LPP)

    本文基于EEDS协议建立了新的跨层优化LPP模型，因此，LPP的限制条件与成本函数必须满足EEDS协议。EEDS协议中建立了一个能效树，本模型的首要目标是最大化网络的生命期，另一个重要目标是最小化延迟。

    假设网络中共n个节点(包括sink节点)，sink的序号设为1，设d_ij表示节点i和节点j之间的距离，1≤i，j≤n，设R表示节点的单跳传输范围，E_i表示节点i(1≤i)的剩余能量。

2.1 成本函数

    EEDS协议的主要目标是最大化网络生命期，首先建立一个能效树，树中的每个节点选择能量最多的父节点来进行数据传输，从而实现了整体网络生命期的优化。设EC_i为节点i从子节点接收数据包所消耗的能量，E_i表示节点i的剩余能量。

    应考虑如下因素：

    (1)对于剩余能量较高的节点，应最大化其EC_i；反之，对于能量低的节点，则最小化其EC_i。

    (2)E_i高的节点，其子节点应该更多。

    综上，应最大化每个节点的EC_i×E_i。因此，成本函数则是最大化所有节点EC_i×E_i的总和：

    LPP模型另一个目标为最小化延迟，延迟定义为一个数据包到达sink节点所需的总时间。根据EEDS协议，每个中间节点需将其本轮接收的所有数据均传至其父节点，最终所有数据传至sink节点。将sink节点表示为node-1，为了最小化延迟，node-1的传输时间(t1)必须最小化。因此，第二个目标表示为：

    LPP模型可通过式(4)求解，或者将延迟作为一个限制条件来求解网络生命期的最大值。

2.2 能效树的限制条件

    为了表示节点i与节点j之间的父子链接关系，定义二值变量x_ij为：

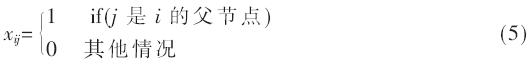
    对于两个节点组成的节点对，仅有一个父节点与一个子节点，或者两节点间无关系，因此：

式(6)表示两个节点为父子关系时，x_ij与x_ji中至少有一个为1；两者无关系时为0。

    每个节点i(包括sink节点)仅有一个父节点：

    设节点通信范围为R，节点仅可与其通信范围内的节点通信。对于一对节点(i与j)，如果距离大于R，则无法建立链接，表示为：

    设距离为d的两个节点间发送k比特数据的能耗为E_Tx，而接收k比特数据所需能量为E_Rx：

2.3 TDMA调度器限制条件

    引入一个二值变量：在一个时间间隙中，一对节点间是否有数据传输，表示为：

其中k是i的子节点。

    将式(23)代入式(24)：

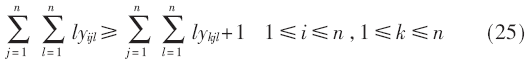
    因此LPP的成本函数为式(2)～(4)，限制函数为式(5)~(11)、式(15)、式(18)~(22)、式(25)。

3 仿真试验与结果

3.1 试验环境与试验平台

    使用LINGO求解器来求解LPP模型。本实验中，设置LINGO自动选择合适的方案。利用Visual Basic将本算法编程实现并产生可执行程序(驱动程序)，驱动调用LINGO求解器来求解。

3.2 参数设置

    试验中，设网络进行1 000个周期活动。如果1 000个周期小于TP，则使用能效树；否则，使用TP。每轮结束，驱动计算每个节点的剩余能量，将剩余能量为0的节点删除。若该轮数据传输成功，则使用更新的输入参数调用LINGO求解器。

    采用不同的网络参数建立多组试验：每组配置中，传感节点在不同维度上随机分布，但所有网络配置中，sink均处于几何中心位置；每组试验测试30个不同的网络结构，每组试验的结果为30次试验的平均值，其置信水平为0.95。采用文献[8]的能量模型，参数设置如下：节点通信范围(R)：15 m；电气能耗(eelec)：50(nJ/bit)；sink的起始能量：100 J；各节点初始化能量：2 J；控制数据包大小：40 B；数据包大小：100 B；放大器能耗：100(pJ/bit/m²)。

    试验中比较参数包括：网络生命期、总吞吐量与延迟。生命期设为：从开始直至目标区域的网络覆盖率降至75%的时间。

3.3 试验结果与分析

    将EEDS协议的仿真结果与本文模型优化的结果(仅考虑第一个成本函数)进行比较。

    第一组试验设为：将10个节点随机分布于大小为50 m×50 m的方形区域，试验结果如图2所示。从图2可看出两个解的变化趋势相仿，但LPP的解优于EEDS仿真的解。在250 s后，LPP的节点存活数量为5，而EEDS仿真的结果仅为150 s，即降至5个节点。LPP解比EEDS仿真的解性能提高了66%。

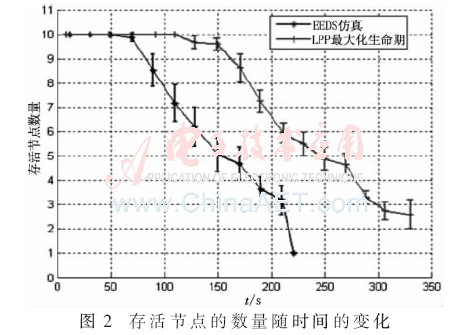
    图3所示为LPP解与EEDS仿真的覆盖率的比较，可看出LPP的覆盖率较优：250 s之后LPP解的覆盖率降至60%，而仿真在190 s即降至60%。LPP解比EEDS仿真的性能提高了31.5%。

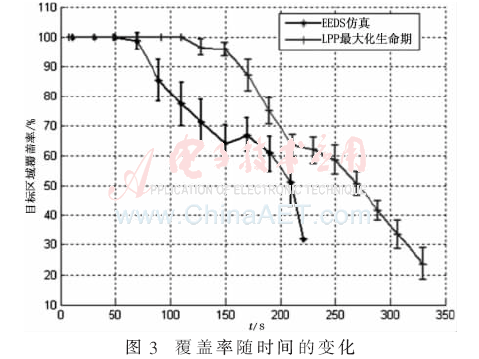
    图4所示为网络生命期随网络密度变化的试验结果。可看出两个解的性能接近，生命期均随着网络密度的提高而提高。原因在于：当网络密度较高时，节点间距离较近，从而传输数据消耗的能量也较少。此外，高密度下节点的邻居节点数量也较多，因此，每轮中节点可选择不同的邻居节点进行传输。反之，如果密度较低，每个节点仅有一个邻居节点，因此该节点消耗较多的能量，导致其能量可能较早耗尽。

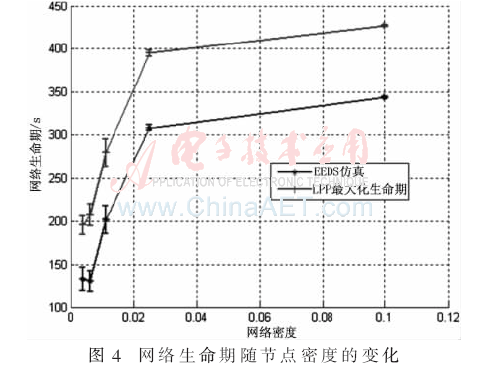
    从图4中可看出，LPP解的生命期优于EEDS仿真解，当网络密度为0.025 node/m²时，LPP解的网络生命期为395 s，而EEDS的生命期仅为308 s。LPP解的性能比EEDS仿真提高了28.3%。其原因在于：LPP模型建立的能效树假设网络的全局信息是已知的，在此基础上建立了一个最优树，而EEDS仿真基于局部信息建立，无法获得全局最优解。

4 小结

    现有的EEDS协议通过建立跨层优化模型提高了网络生命期，本文基于EEDS协议建立了优化模型与目标成本函数，并设计一些合理的限制条件来提高求解速度。试验结果证明，本优化模型进一步提高了EEDS协议的网络生命期性能，并降低了数据传输的延迟。

参考文献

[1] 钱志鸿，王义君.面向物联网的无线传感器网络综述[J].电子与信息学报，2013，35(1)：215-227.

[2] 吕西午，刘开华，赵岩.基于Zigbee的无线监测系统设计与实现[J].计算机工程，2010，36(5)：243-244.

[3] 崔伟，冯媛，甘勇，等.基于WSN的农产品物流跟踪监控系统[J].通信技术，2009，41(9)：140-141.

[4] 王翔宇，沈冬远.传感器网络技术在未来战争中的发展及应用[J].通信技术，2008(11)：227-229.

[5] AL-KHDOUR T A，BAROUDI U.An energy-efficient distributed schedule-based communication protocol for periodic wireless sensor networks[J].Arabian Journal for Science and Engineering，2010(35)：155-168.

[6] 王陆江，张伟，张敬忠.基于TDMA的无线传感器网络时隙分配算法[J].计算机工程与设计，2008，29(7)：1706-1708.

[7] BOUKERCHE A，CHENG X，LINUS J.A performance evaluation of a novel energy-aware data-centric routing algorithm in wireless sensor networks[J].Wireless Networks，2005，11(5)：619-635.

[8] HEINZELMAN W B，CHANDRAKASAN A P，BALAKRISHNAN H.An application-specific protocol architecture for wireless microsensor networks[J].Wireless Communications，IEEE Transactions on，2002，1(4)：660-670.