0 引言

　　由于接入电网的非线性负载越来越多，且负载不断变化，这必然导致电网上的谐波越来越复杂，被污染的电网给设备的安全可靠运行埋下了巨大的安全隐患。有源电力滤波器能够通过产生参考补偿电流有效抑制电网谐波。在生成参考电流方面，很多方法已经被提出，如：快速傅里叶变换法(FFT)[1]、瞬时无功功率算法[2]、人工神经网络算法(ANNs)、小波变换(WT)[3-4]和自适应滤波(AF)[5]等，但效果都不是很理想。基于LMS的自适应滤波(AF)利用自适应噪声对消的原理，优点是低成本，易于数字化实现。然而，它的收敛速度、动态响应速度和稳态误差之间存在固有矛盾[6]。王宗臣[7]提出的一种变步长LMS自适应滤波算法改善了收敛精度，但依然存在输入信号自相关矩阵的特征值分布影响收敛速度的问题，进而影响其动态响应速度。由于提升小波变换具有很好的去相关能力，能够有效地减小输入信号自相关矩阵的谱动态范围，进而使LMS算法的动态响应速度和收敛速度得到提高。为此，提出了将提升小波变换和变步长LMS相结合的自适应谐波检测新算法(Lifting Wavelet Transform and Variable Step LMS，LWT-VSLMS)，增强了传统自适应谐波检测的实时性和稳定性，并在设计的电力谐波检测电路系统上得到了验证。

1 提升小波算法和变步长LMS算法

　　小波变换具有良好的时频局部特性及多分辨分析特性，通过对自适应滤波器的输入进行正交变换，从而使自相关特征矩阵的谱动态范围得到降低，LMS算法动态响应速度和收敛速度可以有效提高，在与自适应结合的变换方式中，更多采用离散小波变换算法(Mallat)[8]。Mallat算法的分解和重构如图1所示。

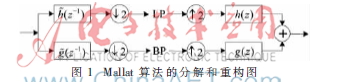
　　Mallat算法相当于使用有限长滤波器的子带变换，正变换使用分解滤波器，接下来进行二抽取。反变换先进行插值，再使用合并滤波器h和g。这样原信号可以得到完美重构，当且仅当h、g满足完美重构条件：

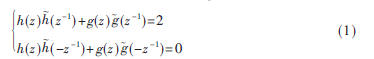
　　1.1 提升小波算法

　　提升小波变换算法相对于传统的小波变换而言，可以直接在时域进行分解，突破了伸缩平移不变性等局限，使小波变换更加易于在即时应用中实现[9]。提升小波变换算法原理如图2所示。

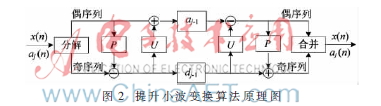
　　提升算法的基本步骤是：

　　(1)分解：首先按奇、偶样本将原始信号序列分解成两个部分；

　　(2)预测：预测步骤用式(2)的差值来代替奇序列，该差值被定义为细节信号，其中P是预测算子。因此，预测步骤可以看作是一次高通滤波。这一过程由下式得：

　　dj-1[n]=xo[n]-P(xe[n])(2)

　　(3)更新：该步用一个近似的平滑的原始数据代替偶序列，其中U是更新算子。由于平滑的信号包含更少的高频成分，所以该操作可以看作一次低通滤波。更新的等式如下式：

　　aj-1[n]=xe[n]-U(dj-1[n])(3)

　　(4)归一化：近似信号和预测信号在变换的最后必须归一化。提升步骤对于正变换的分解或分析描述由图2所示。更新和预测阶段可以变成一对，但有时在一个提升步骤中可能不在一起。在反变换中，更新之后是预测，最终奇、偶序列合并为一个数据流。反变换的等式如下：

　　xe[n]=aj-1[n]-U(dj-1[n])(4)

　　xo[n]=dj-1[n]-P(xe[n])(5)

　　1.2 提升小波自适应算法

　　提升小波自适应算法用自正交化方法提高LMS的收敛性能。首先通过提升小波变换对自适应滤波器的输入信号进行正交小波分解，该步骤等价于用一组带通滤波器对信号进行处理，把信号分成了一些不同频带的子带，再对每一个子带利用LMS算法进行处理。假设滤波器在n时刻的输入为x(n)，经过延迟之后的输入向量x0=[x(n) x(n-1)…x(n-N+1)]T。用提升小波变换对输入信号进行分解。信号x0的j级细节信号用Dj(j=1，2，…，J)表示，Xj描述信号x0的j级近似信号。Wj(j=1，2，…，J)是第j级细节信号对应的自适应滤波器的权向量。信号x0在进行J次分解后，近似信号对应的自适应滤波器的权向量用U表示。提升小波自适应滤波算法的结构如图3所示。

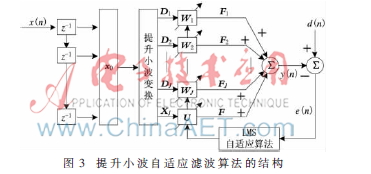
　　由图3可看出：提升小波变换的自适应算法实质上可以认为是j+1个自适应算法的累加，第j个自适应滤波器在n时刻的输出用Fj表示，输入信号为j级细节信号Dj。

　　1.3 改进的变步长LMS算法

　　经过提升小波变换后虽然能够有效地减小输入信号自相关矩阵特征值的分布范围，提高LMS算法的动态响应速度和收敛速度，但是收敛速度和稳态误差这一固有矛盾仍然不能得到解决。因此，采用变步长的思想，构建了步长因子μ与误差信号e之间的非线性函数关系，迭代表达式如下所示：

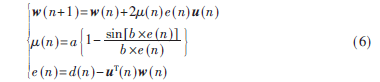
　　其中：μmax=b×e(n)=3π/2，amax=0.8/λmax，在0＜a＜amax范围内，算法收敛。这样改进的变步长LMS算法不仅具有较好的收敛精度，还能够大大提高收敛速度和动态响应速度。

　　2 基于提升小波变换的变步长LMS算法

　　基于小波提升变换的变步长LMS算法(LWT-VSLMS)用于谐波检测的原理图如图4所示。

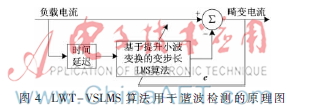
　　改进算法的步骤如下：

　　(1)选择参数和初始条件：选择合适的小波基和分解层数J，则滤波器的阶数L=k·2J，其中k为正整数，实际应用情况下可选择L=2J+k，(k=2～5，k∈N)；初始权值w(0)=0或由先验知识确定；平滑因数0＜β＜1；初始误差e(0)=1。

　　(2)计算自适应滤波器的输出y(n)：

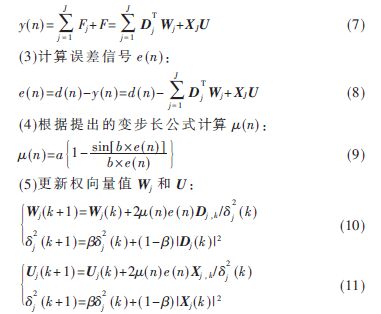
　　其中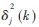，表示j级细节信号的功率估计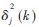，代表j级近似信号的功率估计。

3 电力谐波检测电路系统

　　为精确测量出电网上的谐波，并将改进的算法应用到实际中，本文采用DSP处理器TMS320F2812作为采集和运算核心设计了电力谐波检测电路系统，主要包括互感器、信号调理电路、A/D转换模块MAX125、外扩存储器CY7C1041V33、RS232转USB模块、LCD显示器和上位机。检测电路硬件电路结构如图5所示。数字信号处理器TMS320F281属于32位定点控制器，采用了高性能的CMOS技术，集成度非常高，具有强大的运算功能。考虑到在做一些较复杂的运算时，受内部RAM容量的限制会导致运算速度降低，需要外扩RAM来提高运算速度。外扩RAM芯片选用CYPRESS公司生产的CY7C1041V33，其具有256 K×16 bit的存储容量，可以直接与DSP的数据总线和地址总线相连[10]。

　　设计的硬件电路系统适用于三相电的谐波检测，具有3路电压和3路电流检测通道，根据待检测电力的电压和电流范围，采用电压互感器进行降压（至标称值为100 V），采用电流互感器进行降流（至标称值5 A）。利用电压传感器SPT304和电流传感器SCT354将被测信号与处理器隔离，并把待测的电压与电流转换到2.91 V的额定电压输出给DSP处理器[11]。DSP处理器TMS320-F2812控制14位的模数转换器MAX125实现信号的高速采集和转换，通过采样处理后进行FFT运算将时域信号转换到频域，实时地检测出电网1～50次谐波的电力参数，并实时显示在LCD显示屏上。同时，将数据通过RS232转USB接口发送到上位机作进一步处理。设计的采样电路具有动态响应快、测量精度高和传递频带宽等优点。

4 实验与分析

　　为了验证提出的改进算法性能，利用设计的电力谐波检测电路作为实验平台，将本文设计的算法与传统的LMS算法进行了对比。实验环境：搭建一个三相三线的并联有源电力滤波器的模型，三相电源线电压为：380 V/50 Hz，负载为感性负载，其中负载电阻R=8 Ω，L=2 mH。

　　4.1 负载电流波形的谐波分析

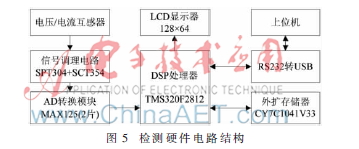
　　当0.1 s时，负载电路的电阻电感变为R=4 Ω，L=1 mH。采样频率为20 kHz，提升算法选择DB8小波进行6层分解，得到传统的自适应算法对a相负载电流波形的谐波分析，包括：负载电流、基波电流、谐波电流和误差，结果如图6所示，其显示范围均在0～0.2 s之间。

　　从图6中可看出：自适应算法在稳态下可以从负载电流中有效地检测出基波电流，稳态误差在0～0.1 s和0.1～0.2 s之间，都小于1%。但是瞬时响应时间大于一个周期，并且瞬时误差很大。

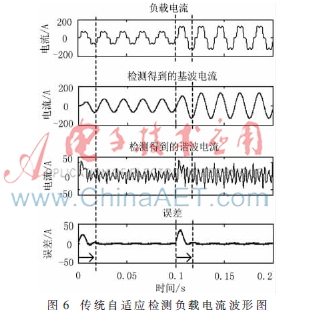
　　采用LWT-VSLMS算法对a相负载电流波形进行谐波分析，结果如图7所示。

　　从图7中可看出：LWT-VSLMS算法在稳态下可以从负载电流中有效地检测出基波电流，稳态误差在0～0.1 s和0.1～0.2 s之间，都小于0.5%。瞬时响应小于1/4个周期。

　　4.2 基波电流FFT分析

　　通过对负载电流及两种算法检测到的基波电流进行FFT分析，结果如图8所示。

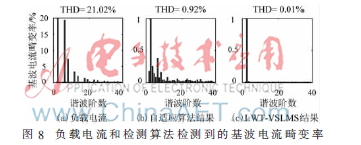
　　由此可得到电流中的THD值，负载电流的THD为21.02%，传统的自适应和LWT-VSLMS算法检测到的基波电流略有增加，THD分别为0.92%、0.01%。可见改进后的算法具有更高的稳态精度。

5 结论

　　本文提出的提升小波变换和变步长LMS相结合的自适应谐波检测新算法对输入谐波电流进行正交变换，有效减少了输入数据的互相关，并加快LMS的收敛速度，同时也保证了较小的稳态误差。将改进的算法应用到基于DSP设计的电力谐波检测电路系统上，通过实验证实了设计的电力谐波检测电路系统能够准确测量电网上的谐波参数，改进的算法在稳态下谐波检测过程中具有有效性，在1/4个周期内跟上负载电流的变化，并且稳态误差小于0.5%。另外，该算法的计算复杂度远低于传统的小波自适应，相比于传统的自适应算法，该算法不仅能够更有效地提取谐波电流，为有源电力滤波器提供准确可靠的数据，而且能更快速地跟踪谐波电流，便于抑制谐波，为提高电网质量提供技术保障。

　　参考文献

　　[1] 桑松，柴玉华，孙影.基于小波变换和快速傅里叶变换的谐波检测[J].电测与仪表，2012，49(7)：29-32.

　　[2] 王立峰，郑建勇，梅军，等.基于瞬时无功功率理论谐波电流并行检测算法研究[J].华东电力，2011，39(6)：890-894.

　　[3] 曾瑞江，杨震斌，柳慧超.基于小波变换的电力系统谐波检测方法研究[J].电力系统保护与控制，2012，40(15)：35-39.

　　[4] 臧川，江冰，薛心怡，等.基于小波优化神经网络的故障定位算法研究[J].电子技术应用，2014，40(6)：55-58.

　　[5] 黄彬，邰能灵，傅晓红，等.基于混合滤波器的大型船舶电力系统谐波抑制分析[J].上海交通大学学报，2011，45(6)：787-792.

　　[6] 李锋，邱陈辉，徐祖强.基于改进DLMS算法的自适应FIR滤波器设计[J].计算机工程与设计，2014，35(3)：895-899.

　　[7] 王宗臣，包志华，张士兵，等.一种改进的变步长LMS谐波电流检测算法[J].电力系统保护与控制，2012，40(22)：73-77.

　　[8] 周龙华，付青，余世杰，等.基于小波变换的谐波检测技术[J].电力系统及其自动化学报，2010，22(1)：80-85.

　　[9] 田宝华，李宝峰.二维离散小波提升变换算法的并行结构设计[J].计算机应用，2011，31(12)：3366-3369.

　　[10] 薛志远，朱浩，张铁军，等.一种基于串口通信的DSP调试平台设计[J].微电子学与计算机，2013，30(12)：57-60.

　　[11] 王瑞平，彭云峰.基于DSP嵌入式数据采集与处理系统设计与实现[J].计算机测量与控制，2014，22(6)：1932-1934.